MATLAB仿真实验
在MATLAB 中编写程序,产生一个 DSB 信号(具体参数根据自己制定的实验方案设置),绘制信号的时域波形图和频谱结构波形图,并对 DSB 信号的数据统计特性进行分析。
该部分不仅完成了DSB调制,同时在此基础上成功完成了DSB解调。
流程图如下:
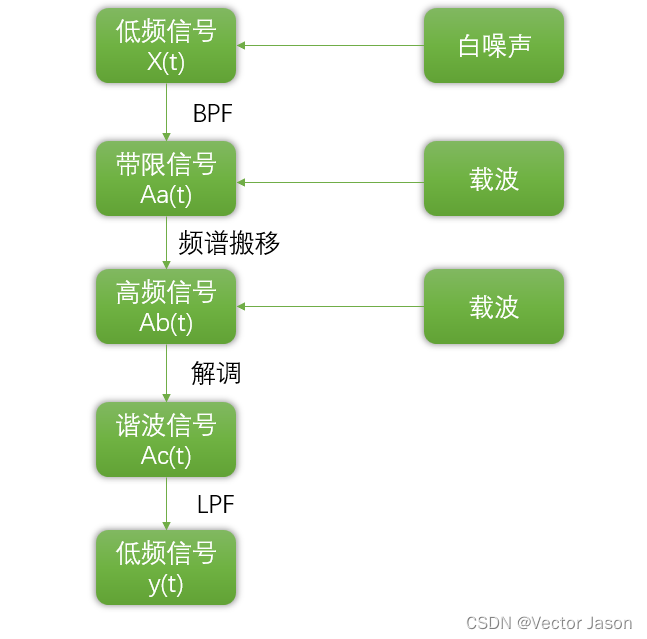
图1 DSB调制与解调流程图
代码详见DSB.m文件中。
clc
clear
close all;
%-------------------------设置信号参数------------------------
fs=30.72e3; % 采样频率
F=1000; % 频率
Fc=4000; % 载波频率
N=30720; % 采样个数,N变大,时间长度变长
dt=1/fs; % 时间间隔,fs变大,时间间隔变短,曲线变光滑
t=0:dt:(N-1)*dt; % 时间向量,fs变大,时间长度变短
%------------------------------------------------------------
%---------------------产生输入信号x--------------------------
% x(t)时域
n=wgn(1,N,0)/5; % 产生高斯白噪声
x=cos(2*pi*F*t)+n; % 获取x(t)的采样点
figure; % x(t)为加噪后的有用信号
subplot(221)
plot(t,x);
axis([2e-2 4e-2 -2 2]);
xlabel('时间(t)');
ylabel('幅值(V)');
title('x(t)时域');
%------------------------------------------------------------
%-------------------------x信号的分析------------------------
disp('x(t)的均值为');
En=mean(x); % 求x(t)均值
disp(En);
disp('x(t)的方差为');
Dn=var(x); % 求x(t)方差
disp(Dn);
freq=fft(x,N); % 做离散傅里叶
freq_d=abs(fftshift(freq));
w=(-N/2:1:N/2-1)*fs/N; % 双边
subplot(222);
plot(w,freq_d);
%axis([-1500 1500 0 30000]);
xlabel('频率(Hz)');
ylabel('幅值(V)');
title('x(t)幅频特性');
[c,lags]=xcorr(x,'unbiased'); % 求出自相关函数
subplot(224);
plot(lags/fs,c); % 在时域内画自相关函数
axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('x(t)的自相关函数');
% x(t)的功率谱密度
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
subplot(223)
plot(labelx,plot_magn); % 画功率谱密度
%axis([0 6.3e5 -50 50]);
xlabel('w');
ylabel('Sn(w)');
title('x(t)的功率谱密度');
%------------------------------------------------------------
%--------------------------带通滤波器------------------------
[bp,ap]=butter(5,[800*2/fs,2000*2/fs]);
[hp,wp]=freqz(bp,ap);
figure;
plot(wp/pi*fs/2,abs(hp));
grid;
%axis([4e2 3e3 0 1]);
title('带通滤波器');
xlabel('频率(Hz)'); ylabel('幅度');
%------------------------------------------------------------
%------------------------产生信号Aa--------------------------
Aa=filter(bp,ap,x); % Aa表示通过BPF后的信号
figure;
subplot(221);
plot(t,Aa);
axis([2e-2 4e-2 -2 2]);
title('Aa(t)时域');
%------------------------------------------------------------
%-----------------------Aa信号的分析-------------------------
disp('Aa(t)的均值为');
En=mean(Aa);
disp(En);%求Aa(t)均值
disp('Aa(t)的方差为');
Dn=var(Aa);
disp(Dn);%求Aa(t)方差
freq=fft(Aa,N);%做离散傅里叶
freq_d=abs(fftshift(freq));
w=(-N/2:1:N/2-1)*fs/N; %双边
subplot(222);
plot(w,freq_d);
%axis([-1500 1500 0 30000]);
xlabel('频率(Hz)');
ylabel('幅值(V)');
title('Aa(t)幅频特性');
[c,lags]=xcorr(Aa,'unbiased'); %求出自相关序列
subplot(224);
plot(lags/fs,c); %在时域内画自相关函数
axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('Aa(t)的自相关函数');
%x(t)的功率谱密度
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
subplot(223)
plot(labelx,plot_magn); %画功率谱密度
%axis([0 6.3e5 -100 50]);
xlabel('w');
ylabel('Sn(w)');
title('Aa(t)的功率谱密度');
%------------------------------------------------------------
%-------------------------产生信号Ab-------------------------
Ab=Aa.*cos(2*pi*Fc*t); % Ab是Aa乘以余弦载波后的信号(即DSB信号)
figure;
subplot(221);
plot(t,Ab);
axis([3e-2 3.5e-2 -2 2]);
title('Ab(t)时域');
%------------------------------------------------------------
%-----------------------Ab信号的分析-------------------------
disp('Ab(t)的均值为');
En=mean(Ab);
disp(En);%求Ab(t)均值
disp('Ab(t)的方差为');
Dn=var(Ab);
disp(Dn);%求Ab(t)方差
freq=fft(Ab,N);%做离散傅里叶
freq_d=abs(fftshift(freq));
w=(-N/2:1:N/2-1)*fs/N; %双边
subplot(222);
plot(w,freq_d);
%axis([-6000 6000 0 1.5e4]);
xlabel('频率(Hz)');
ylabel('幅值(V)');
title('Ab(t)幅频特性');
[c,lags]=xcorr(Ab,'unbiased'); %求出自相关序列
subplot(224);
plot(lags/fs,c); %在时域内画自相关函数
axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('Ab(t)的自相关函数');
%Ab(t)的功率谱密度
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
subplot(223)
plot(labelx,plot_magn); %画功率谱密度
axis([0 6.3e5 -80 40]);
xlabel('w');
ylabel('Sn(w)');
title('Ab(t)的功率谱密度');
%------------------------------------------------------------
%-----------------------产生信号Ac---------------------------
p=cos(2*pi*Fc*t);%余弦波
Ac=Ab.*p; % Ac是Ab再乘以余弦载波后的信号
figure;
subplot(221)
plot(t,Ac);
axis([3e-2 3.5e-2 -2 2]);
title('Ac(t)时域');
%------------------------------------------------------------
%-----------------------Ac信号的分析-------------------------
disp('Ac(t)的均值为');
En=mean(Ac);
disp(En);%求Ac(t)均值
disp('Ac(t)的方差为');
Dn=var(Ac);
disp(Dn);%求Ac(t)方差
freq=fft(Ac,N);%做离散傅里叶
freq_d=abs(fftshift(freq));
w=(-N/2:1:N/2-1)*fs/N; %双边
subplot(222);
plot(w,freq_d);
%axis([-2500 2500 0 30000]);
xlabel('频率(Hz)');
ylabel('幅值(V)');
title('Ac(t)幅频特性');
[c,lags]=xcorr(Ac,'unbiased'); %求出自相关序列
subplot(224);
plot(lags/fs,c); %在时域内画自相关函数
axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('Ac(t)的自相关函数');
%Ac(t)的功率谱密度
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
subplot(223)
plot(labelx,plot_magn); %画功率谱密度
%axis([0 6.3e5 -80 40]);
xlabel('w');
ylabel('Sn(w)');
title('Ac(t)的功率谱密度');
%------------------------------------------------------------
%------------------------低通滤波器--------------------------
[bp,ap]=butter(4,F*2/fs);
[hp,wp]=freqz(bp,ap);
figure;
plot(wp/pi*fs/2,abs(hp));
grid;
%axis([0 2e3 0 1]);
title('低通滤波器');
xlabel('频率(Hz)'); ylabel('幅度');
%------------------------------------------------------------
%----------------------产生输出信号y-------------------------
y=filter(bp,ap,Ac); % y是Ac通过LPF后的信号,从而实现解调
figure;
subplot(221)
plot(t,y);
axis([3e-2 3.5e-2 -2 2]);
title('y(t)时域');
%------------------------------------------------------------
%-----------------------y信号的分析--------------------------
disp('y(t)的均值为');
En=mean(y);
disp(En);%求y(t)均值
disp('y(t)的方差为');
Dn=var(y);
disp(Dn);%求y(t)方差
freq=fft(y,N);%做离散傅里叶
freq_d=abs(fftshift(freq));
w=(-N/2:1:N/2-1)*fs/N; %双边
subplot(222);
plot(w,freq_d);
%axis([-1500 1500 0 15000]);
xlabel('频率(Hz)');
ylabel('幅值(V)');
title('y(t)幅频特性');
[c,lags]=xcorr(y,'unbiased'); %求出自相关序列
subplot(224);
plot(lags/fs,c); %在时域内画自相关函数
axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('y(t)的自相关函数');
%y(t)的功率谱密度
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
subplot(223)
plot(labelx,plot_magn); %画功率谱密度
%axis([0 6.3e5 -120 40]);
xlabel('w');
ylabel('Sn(w)');
title('y(t)的功率谱密度');
%------------------------------------------------------------
时域波形图:
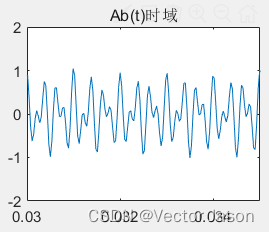
图2 低分辨率DSB调制信号的时域波形
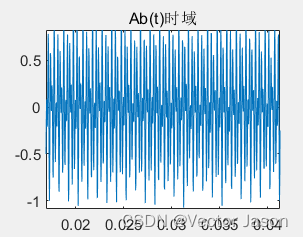
图3 高分辨率DSB调制信号的时域波形
输入信号为加噪后频率为F的余弦信号,通过乘以频率为Fc的余弦载波,绘制图形即可得到DSB时域波形,通过分析DSB时域波形,当分辨率越高时,越能够看见其形成的包络。
频谱图:
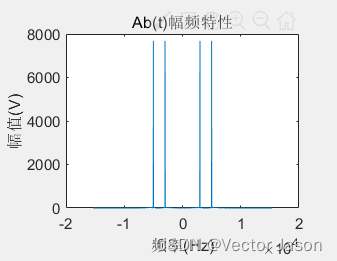
图4 DSB调制信号的频谱结构波形
通过分析DSB幅频特性:由于载波为频率Fc的余弦信号,时域上载波与调制信号相乘,即可在频域实现频谱搬移。
均值:

图5 DSB调制信号的均值
方差:

图6 DSB调制信号的方差
通过分析DSB统计特征:输入信号x(t)幅值为1,通过DSB调制后利用mean(),var()函数即可得到均值,方差。可见其均值为负值,方差较小,波形变化范围相对不大。
自相关函数:
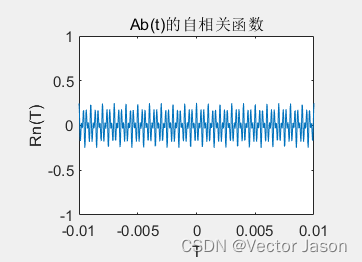
图7 DSB调制信号的自相关函数波形
通过分析DSB自相关函数:在DSB调制下,信号的自相关函数变化具有周期性,相关时间较短,但DSB信号总体上有呈正相关,负相关的趋势。
功率谱密度:
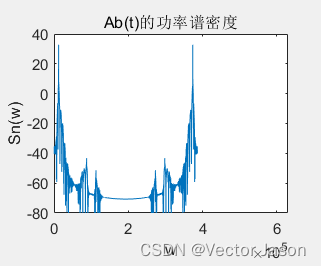
图8 DSB调制信号的功率谱密度波形
通过分析DSB功率谱密度:根据维纳-欣钦定理,对DSB调制中自相关函数进行傅里叶变换即可得到功率谱密度,可见由于BPF的存在滤除了200Khz附近的噪声。由图可知功率谱密度近似以w = 200Khz对称,且在低频,高频处数值更大。
4、分析生物电信号数据
(1.1)心电图(ECG)
数据文件名:ECG.mat
包含25000个数据采样点,250个数据采样点为一组,共100组。
数据示意图:
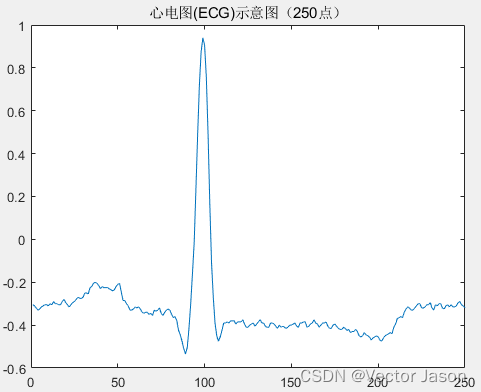
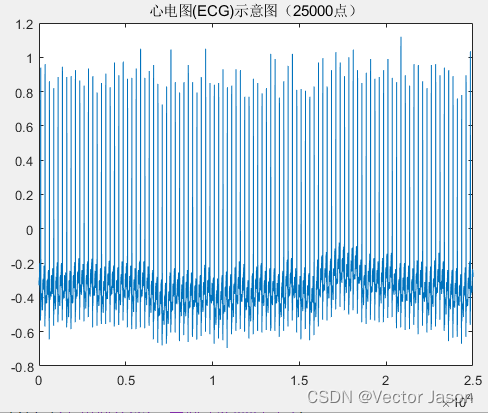
图9 ECG示意图
代码详见Biological.m文件。
%--------------------------------------分析ECG过程--------------------------------------------------
disp('ECG的均值为');
E1=mean(ECG); % 求ECG均值
disp(E1);
disp('ECG的方差为');
D1=var(ECG); % 求ECG方差
disp(D1);
[c,lags]=xcorr(ECG,'unbiased'); % 求出自相关函数
figure(1)
plot(lags,c); % 在时域内画自相关函数
%axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('ECG的自相关函数');
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
plot(labelx,plot_magn); % 画功率谱密度
%axis([0 6.3e5 -50 50]);
xlabel('w');
ylabel('Sn(w)');
title('ECG的功率谱密度');均值:

图10 ECG的均值
方差:

图11 ECG的方差
通过分析ECG统计特征:选取数据文件压缩包,将生物电信号ECG数据作为数组加入到MATLAB工作区中,利用mean(),var()函数即可得到均值,方差。可见其均值为负值,方差较小,波形变化范围相对不大。
自相关函数:
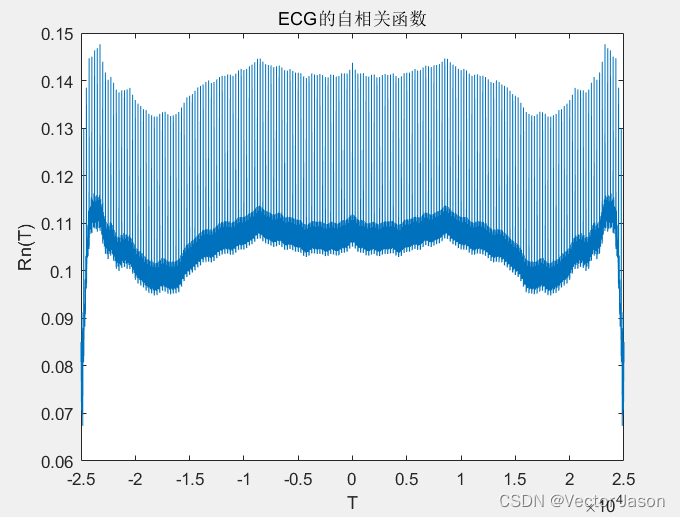
图12 ECG的自相关函数
通过分析ECG自相关函数:相关时间较长,且均大于0,因此ECG生物信号波形整体呈现正相关趋势且持续时间较长。
功率谱密度:
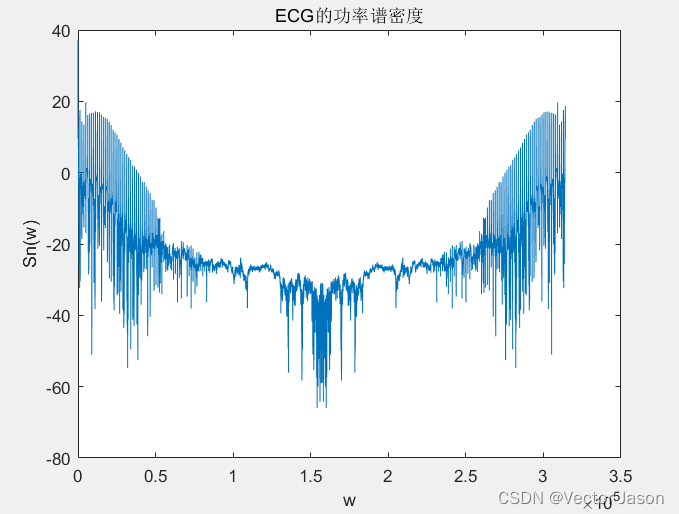
图13 ECG的功率谱密度
通过分析ECG功率谱密度:根据维纳-欣钦定理,对ECG自相关函数进行傅里叶变换即可得到功率谱密度。由图可知ECG的功率谱密度近似以w = 160K rad / s对称,且在低频,高频处数值更大。
(1.2)肌电图(EMG)
数据文件名:EMG.mat
包含22500个数据采样点,45个数据采样点为一组,共500组。
数据示意图:
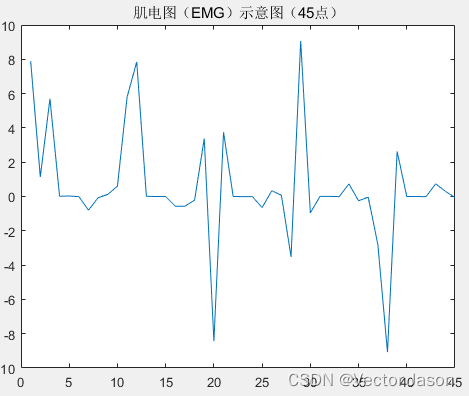
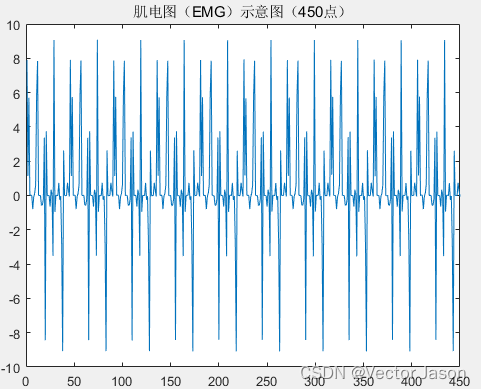
图14 EMG的示意图
代码详见Biological.m文件。
%--------------------------------------分析EMG过程----------------------------------------------------
disp('EMG的均值为');
E3=mean(EMG); % 求EMG均值
disp(E3);
disp('EMG的方差为');
D3=var(EMG); % 求EMG方差
disp(D3);
[c,lags]=xcorr(EMG,'unbiased'); % 求出自相关函数
figure(3)
plot(lags,c); % 在时域内画自相关函数
%axis([2e-2 4e-2 -2 2]);
xlabel('T');
ylabel('Rn(T)');
title('EMG的自相关函数');
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
plot(labelx,plot_magn); % 画功率谱密度
%axis([0 6.3e5 -50 50]);
xlabel('w');
ylabel('Sn(w)');
title('EMG的功率谱密度');
均值:

图15 EMG的均值
方差:

图16 EMG的方差
通过分析EMG统计特征:选取生物电信号EMG数据作为数组加入MATLAB工作区中,利用mean(),var()函数即可得到均值,方差。可见其均值为正值,方差相比ECG而言较大,说明波形变化范围相对较大。
自相关函数:
局部情况(低分辨率):
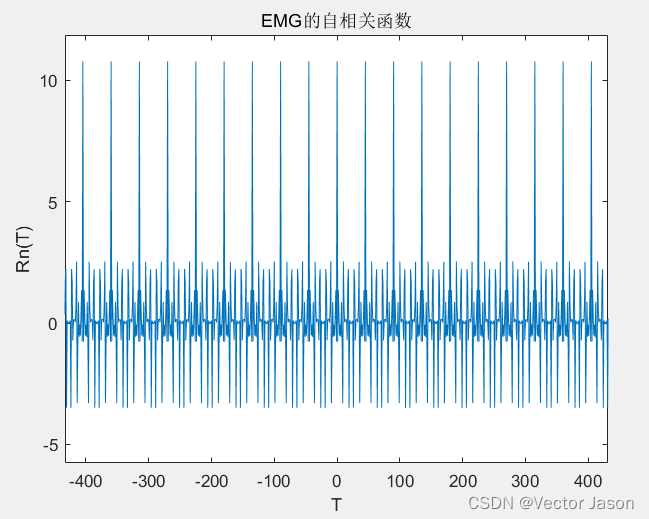
图17 低分辨率下EMG的自相关函数
整体情况(高分辨率):
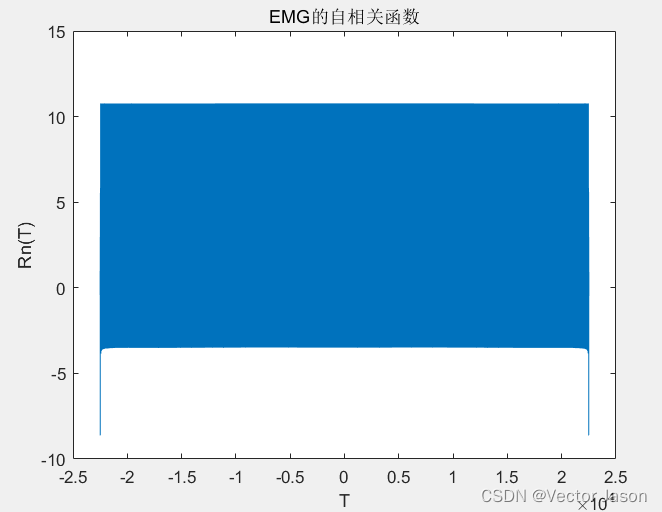
图18 高分辨率下EMG的自相关函数
通过分析EMG自相关函数:相关时间相比ECG较短,但自相关函数幅值较大,因此EMG生物信号波形起伏较大且持续时间短。
功率谱密度:
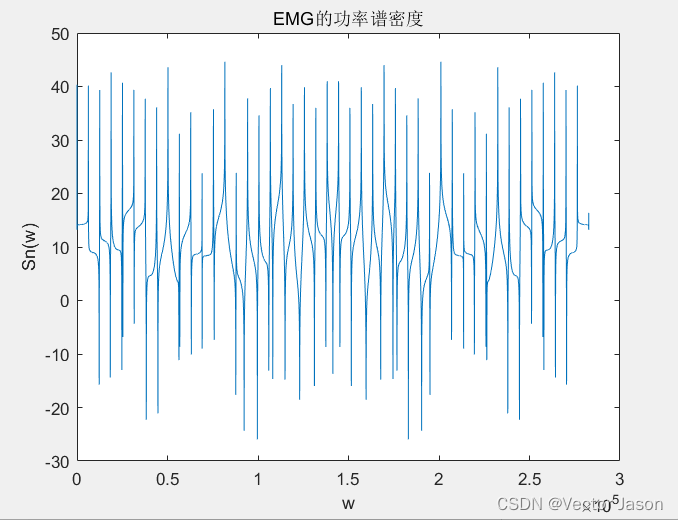
图19 EMG的功率谱密度
通过分析EMG功率谱密度:根据维纳-欣钦定理,对EMG自相关函数进行傅里叶变换即可得到功率谱密度。由图可知功率谱密度变化剧烈,且幅值较大。
(1.3)脑电图(EEG)
数据文件名:EEG.mat
包含26900个数据采样点,1345个数据采样点为一组,共20组。
数据示意图:
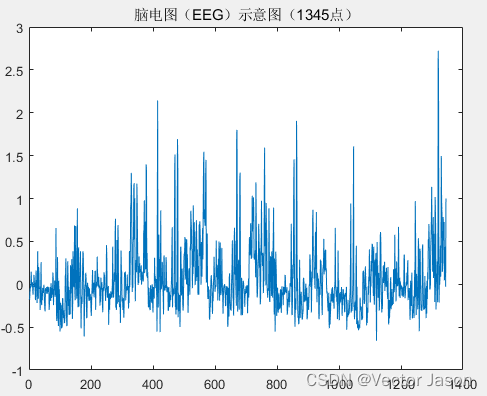
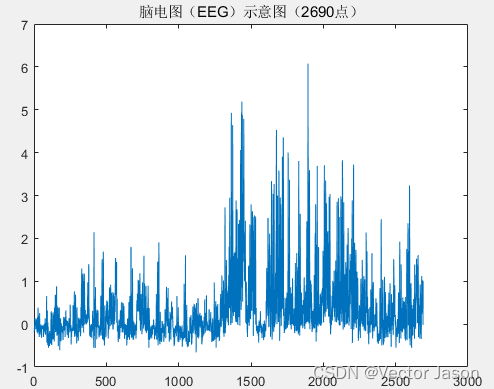
图20 EEG的示意图
代码详见Biological.m文件。
%--------------------------------------分析EEG_1过程-----------------------------------------------
disp('EEG_1的均值为');
E2=mean(EEG_1); % 求EEG_1均值
disp(E2);
disp('EEG_1的方差为');
D2=var(EEG_1); % 求EEG_1方差
disp(D2);
[c,lags]=xcorr(EEG_1,'unbiased'); % 求出自相关函数
figure(2)
plot(lags,c); % 在时域内画自相关函数
%axis([-0.01 0.01 -1 1]);
xlabel('T');
ylabel('Rn(T)');
title('EEG_1的自相关函数');
long=length(c);
Sn=fft(c,long);
labelx=(0:long-1)*2*pi;
plot_magn=10*log10(abs(Sn));
plot(labelx,plot_magn); % 画功率谱密度
%axis([0 6.3e5 -50 50]);
xlabel('w');
ylabel('Sn(w)');
title('EEG_1的功率谱密度');均值:

图21 EEG的均值
方差:
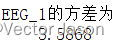
图22 EEG的方差
通过分析EEG统计特征:选取生物电信号EEG数据作为数组加入MATLAB工作区中,利用mean(),var()函数即可得到均值,方差。可见其均值为正值,方差适中,说明波形变化相对平稳。
自相关函数:
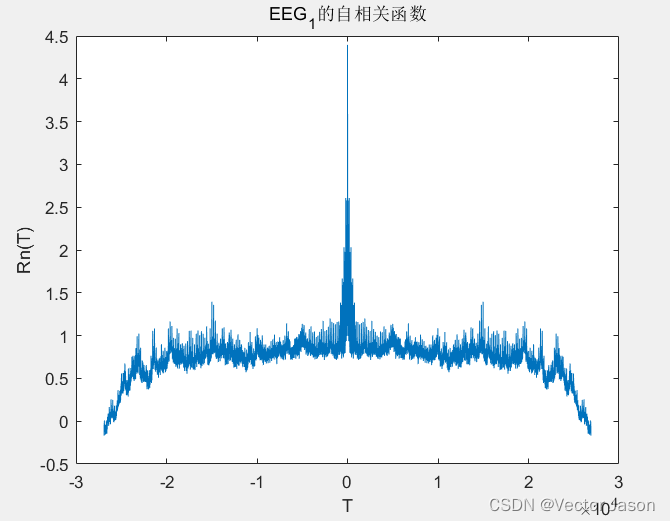
图23 EEG的自相关函数
通过分析EEG自相关函数:相关时间EEG较长,自相关函数幅值适中且总体大于0,近似以T = 0 处对称分布,在T = 0处取得最大值。因此EEG生物信号波形相对平稳且持续时间较长,总体波形在T = 0处将产生一个峰值。
功率谱密度:
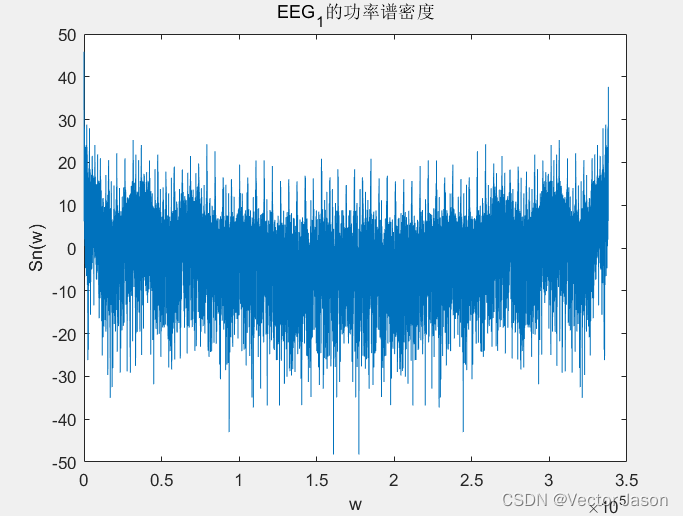
图24 EEG的功率谱密度
通过分析EEG功率谱密度:根据维纳-欣钦定理,对EEG自相关函数进行傅里叶变换即可得到功率谱密度。由图可知功率谱密度近似以170K rad对称,幅值变化相对剧烈。
思考题
为什么要抑制载波?相比与AM信号,DSB信号可以增加多少功率利用率?
答:载波功率不携带信息,抑制载波可以提高功率利用率。AM信号在满调幅情况下的最大调制效率为1/3,而DSB信号的功率利用率为100%,所以可以增加66%的功效。
最后
以上就是虚幻路人最近收集整理的关于模拟调制—DSB信号及生物电信号特性测量分析实验报告MATLAB仿真实验的全部内容,更多相关模拟调制—DSB信号及生物电信号特性测量分析实验报告MATLAB仿真实验内容请搜索靠谱客的其他文章。








发表评论 取消回复