基于Simulink的DSB调制解调系统设计

DSB调制原理

         如果在AM调制模型中将直流A0去掉，即可得到一种高调制效率的调制方式——抑制载波双边带信号（DSB—SC），简称双边带调制信号（DSB）。其时域表达式为

$$s_{DSB}(t)=m(t)cos{w}_{c}t$$
式中，假设m（t）的平均值为0。DSB的频谱与AM的谱相近，只是没有了在±Wc处δ函数，即

$$S_{DSB}=\frac{1}{2}[M(w+w_c)+M(w-w_c)]$$
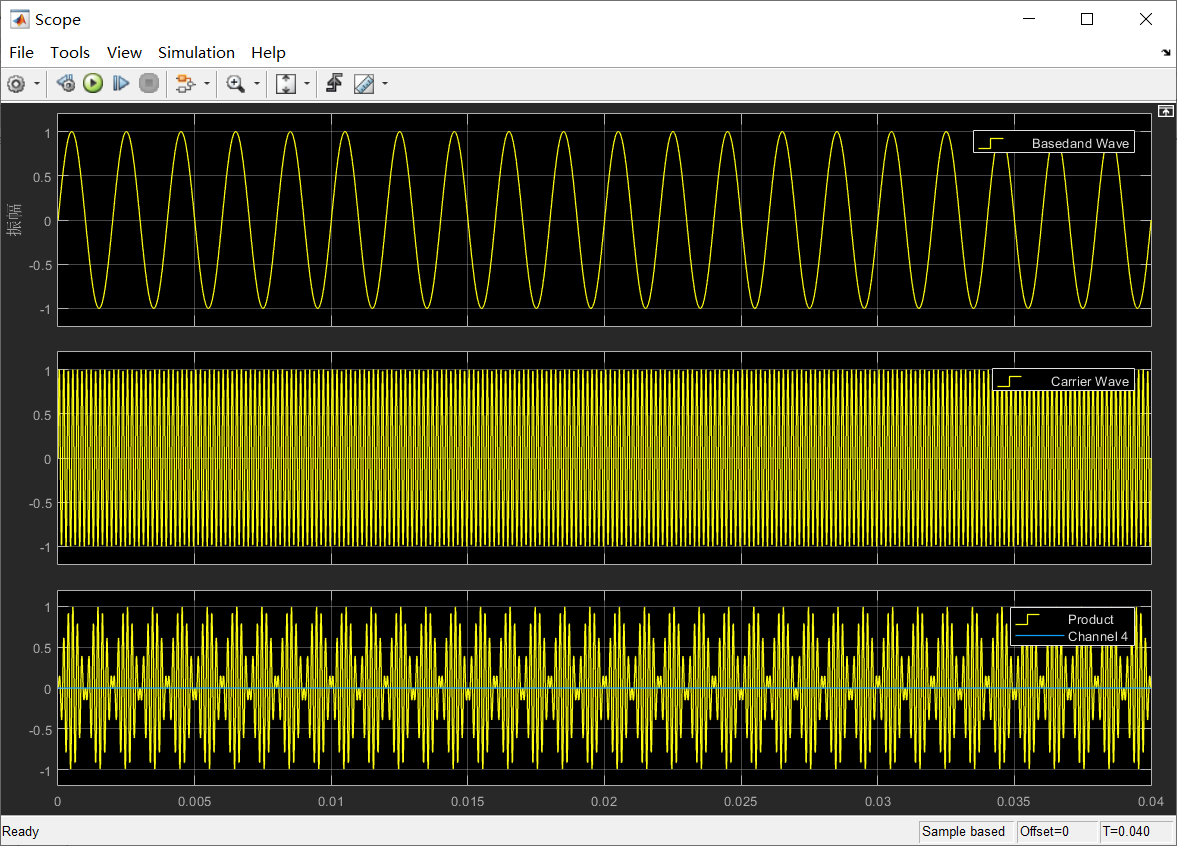
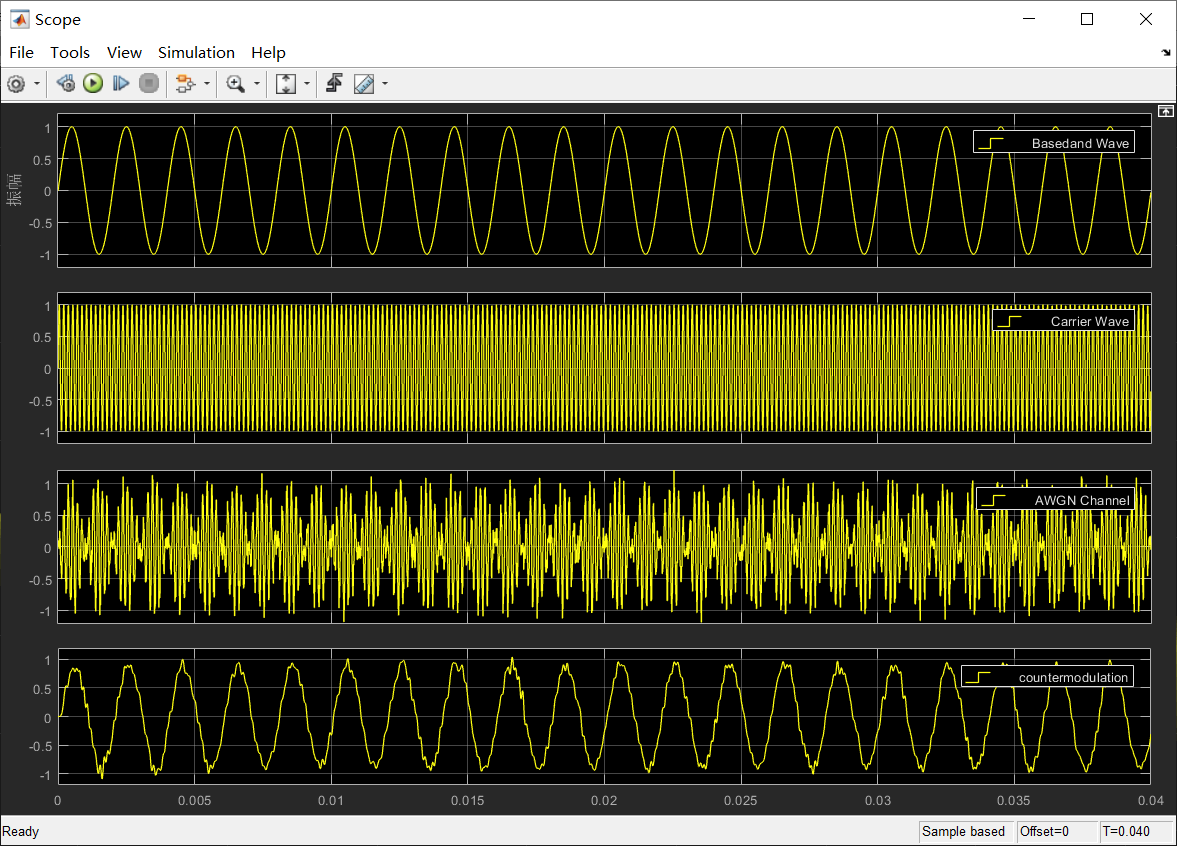
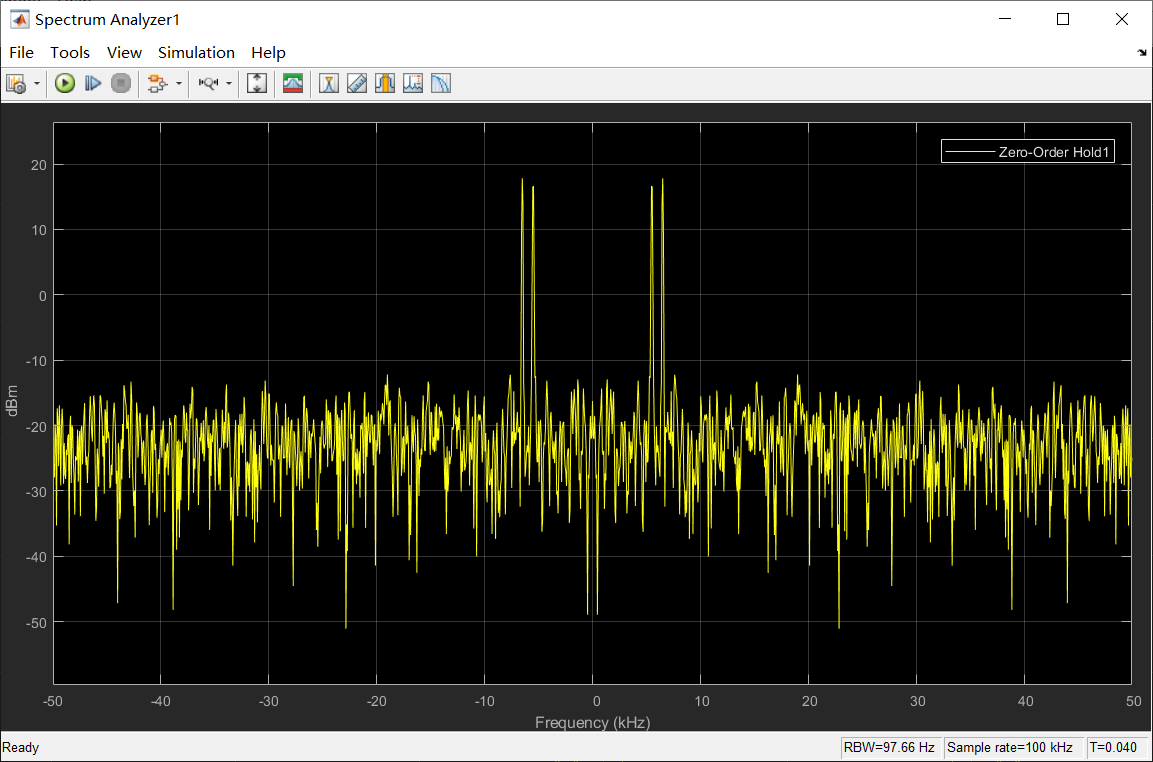
其典型波形和频谱如图所示。

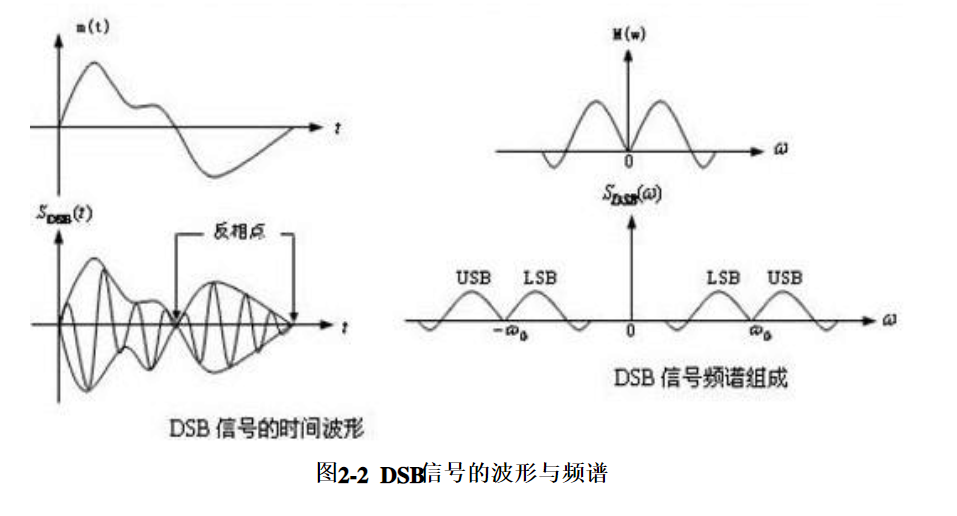
DSB解调原理

         与AM信号相比较，因为不存载波分量，DSB信号的调制效率是100%。DSB的包络不再与调制信号的变化规律一致，因而不能采用简单的包络检波来恢复信号，而采用相干解调来恢复信号。

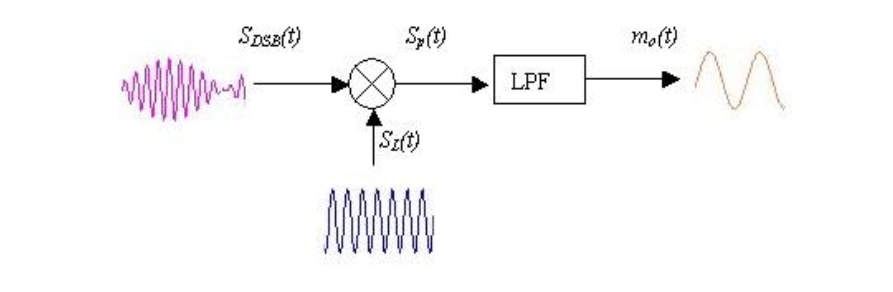
时域解析
$$\begin{gathered} s_{DSB}(t)=m(t)cos{w}_{c}t \\ {s}_p(t)=s_{DSB}cos{w}_{c}t=\frac{1}{2}m(t)+\frac{1}{2}m(t)cos2w_{c}t \end{gathered}$$
经低通滤波器（LPF）后，得

$$m_e(t)=\frac{1}{2}m(t)$$
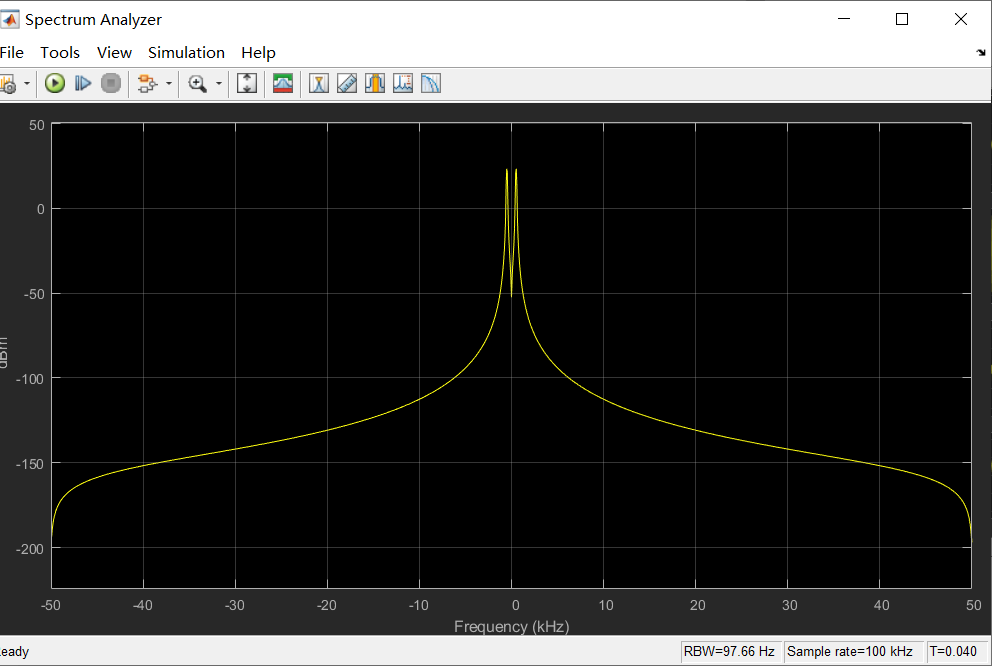
频域过程如图所示

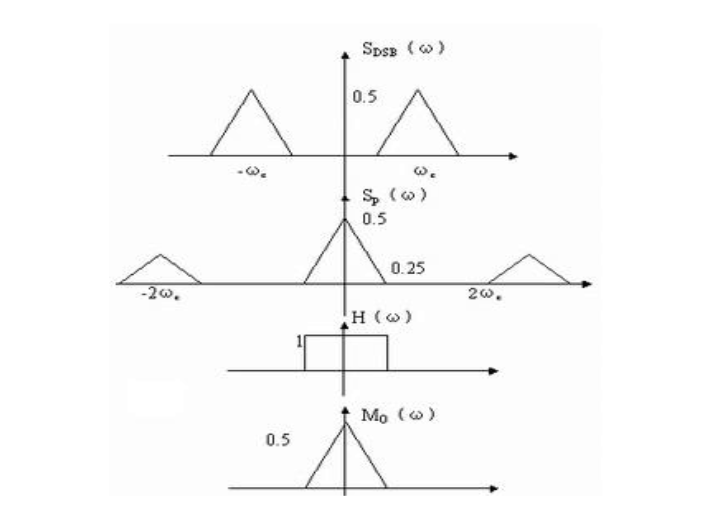
Simulink仿真

         Simulink是MATLAB中的一种可视化仿真工具， 是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。Simulink提供一个动态系统建模、仿真和综合分析的集成环境。在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。本次所用的Matlab版本为2017年版本。

调制模块设计

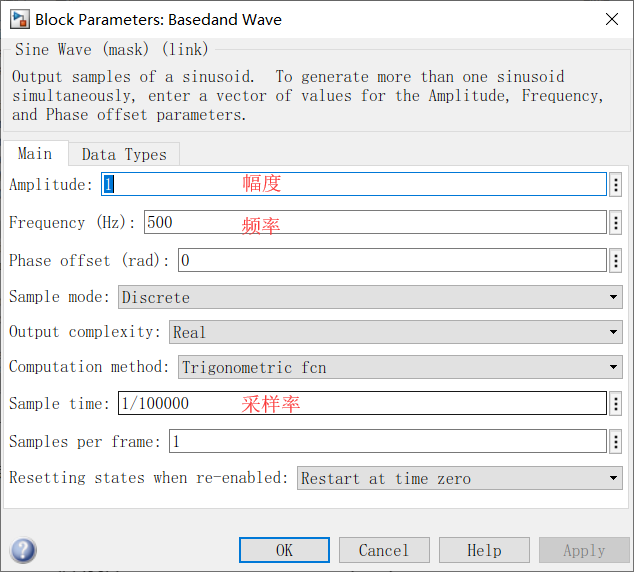
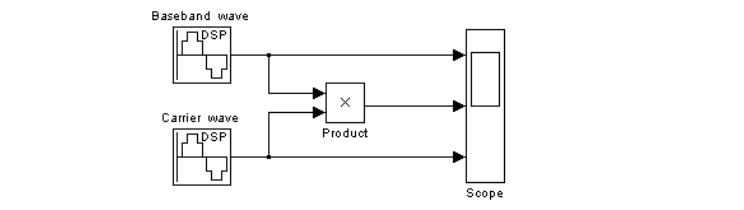
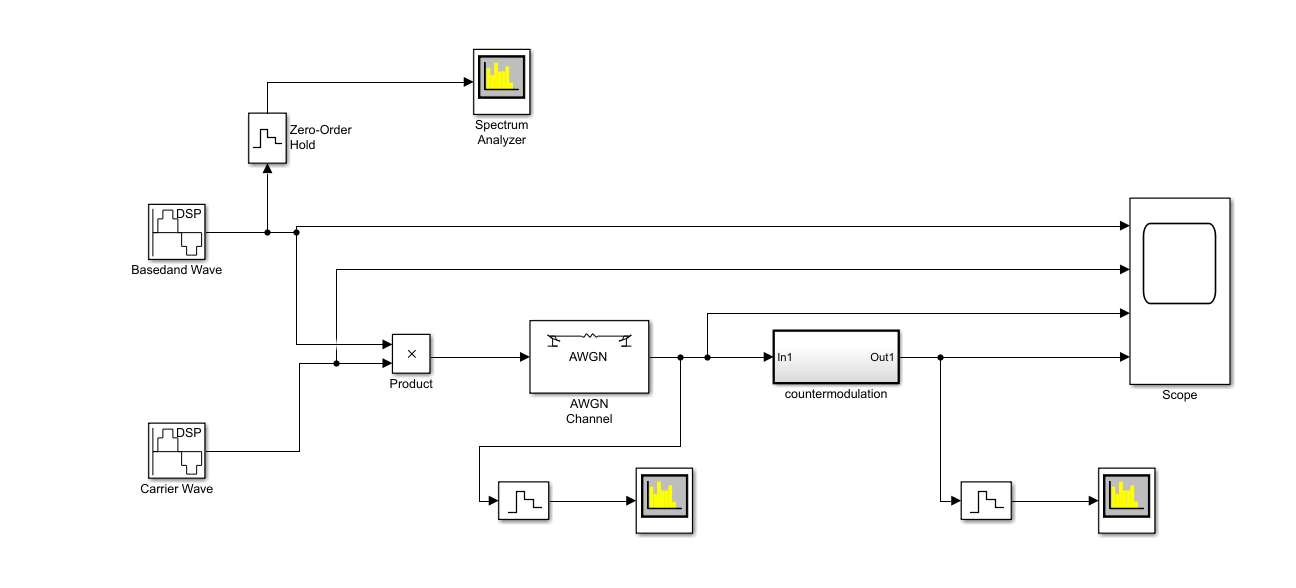
         首先打开Simulink，建立一个仿真空白模型，将DSB信号所需要的模块拖入到空白模型。Baseband wave为正弦基带信号、Carrier wave为正弦载波，均使用离散化的信号。product为乘法器、scope为示波器。操作步骤，连接如下图所示。

模块的查找可以在搜索栏中直接搜索其名称叶即可在对应的库中点击查找。

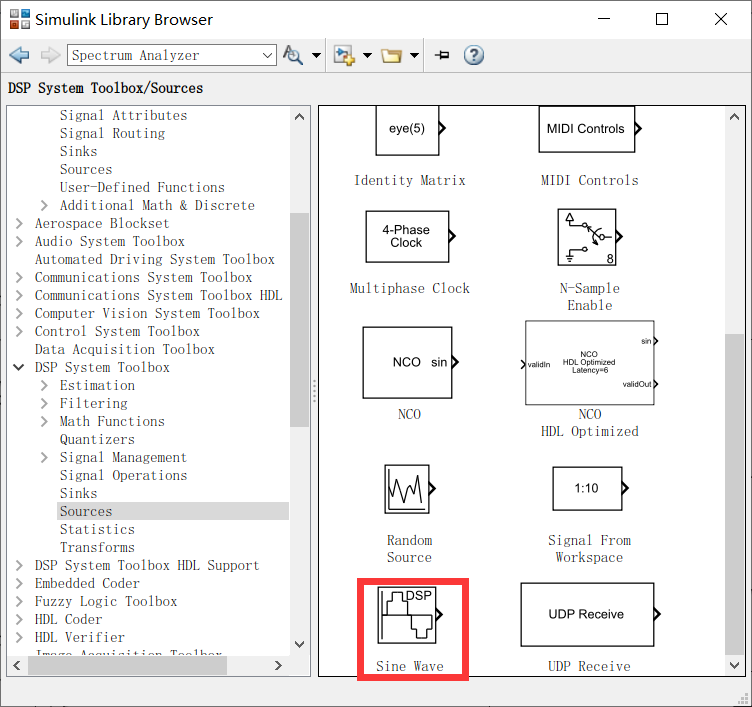
找到模块添加完成后，双击图标设置信号参数

解调模块设计

         DSB信号经过信道传输会叠加上高斯白噪声，所以要在仿真模块前添加AWGN模块。

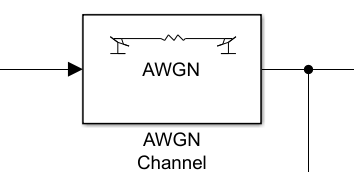
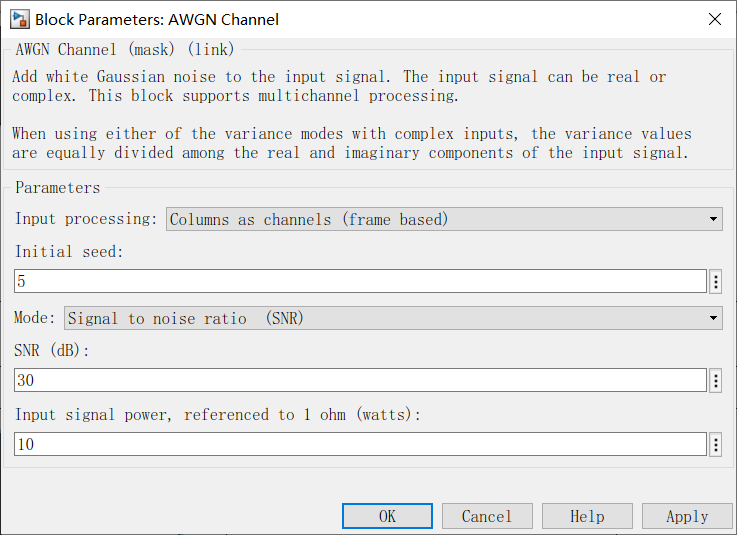
解调模块图

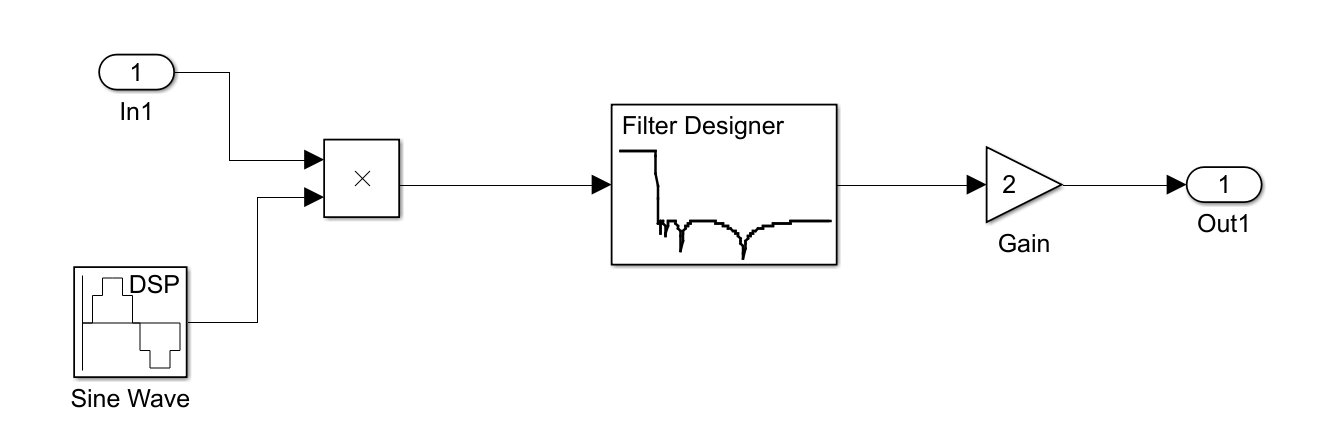
低通滤波器

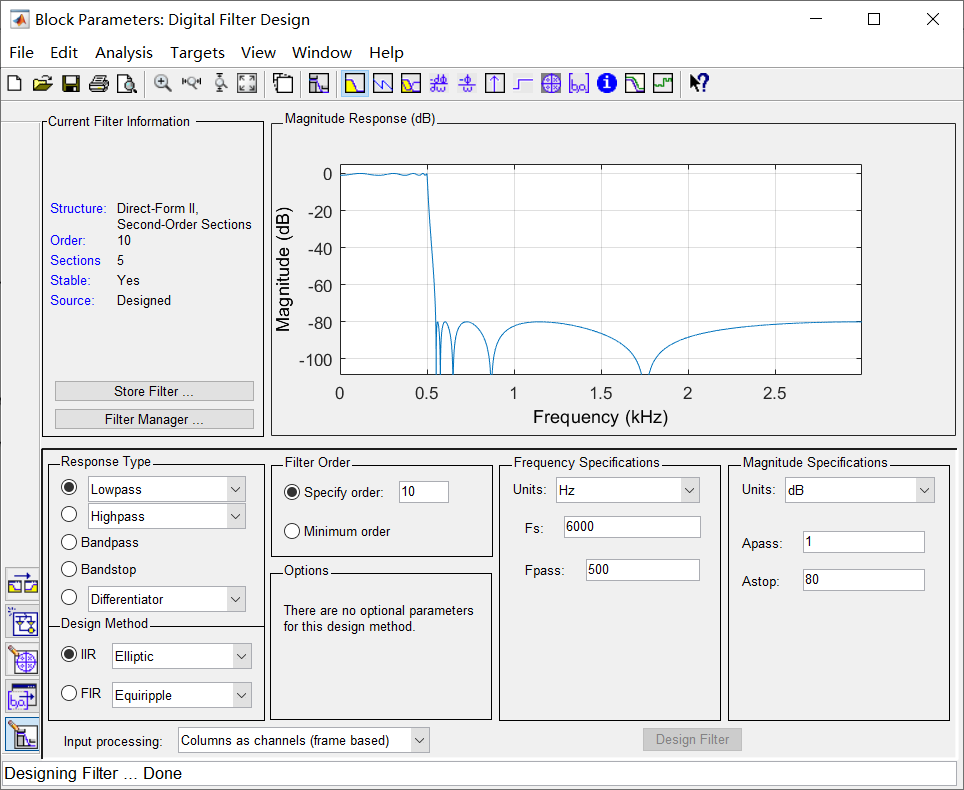
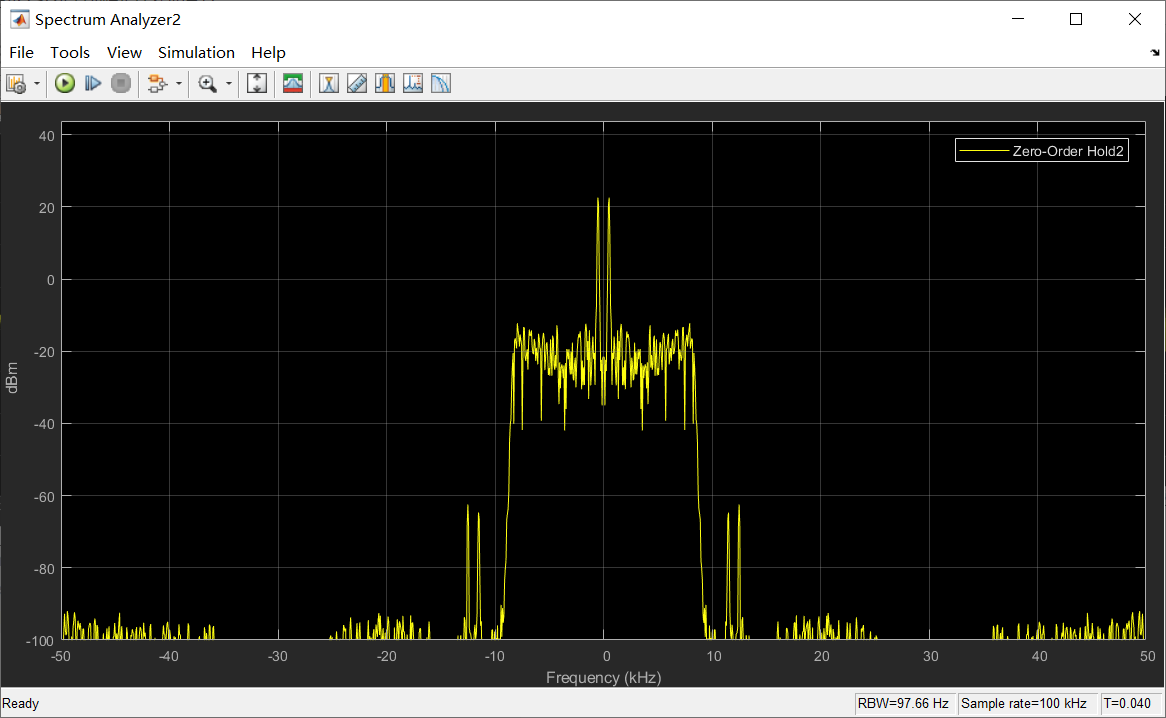
这里我们把解调模块封装为一个子系统，在搜索中输入Atomic Subsystem可添加。然后我们有添加了采样保持器（Zero-Order）和频谱仪（Spectrum Analyzer），来更好的观察信号。

         本文引用了其他文章资料，如有侵权，联系本人会做出修改。版本1.0,2019.10.23 作者小飞。

最后

以上就是震动音响为你收集整理的基于Simulink的DSB调制解调系统设计基于Simulink的DSB调制解调系统设计的全部内容，希望文章能够帮你解决基于Simulink的DSB调制解调系统设计基于Simulink的DSB调制解调系统设计所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。