A*算法 详解与例题

一、简介

A*搜索(A* Search Algorithm)，是一种在图形平面上，对于有多个节点的路径求出最低通过成本的算法。它属于图的遍历和最佳有限搜索算法，同时也是BFS算法的改进之一。

定义起点$s$，终点$t$，从起点(初始状态)开始的距离函数$g(x)$，到终点(最终状态)的距离函数$h(x)$，$h^{\ast }(x)$，以及每个点的估价函数$f(x)=g(x)+h(x)$。

A*算法每次从优先队列中取出一个$f$最小的元素，然后更新相邻的状态。

如果$h\le h^{\ast }$，则A*算法能找到最优解。

上述条件下，如果$h$满足三角形不等式，则A*算法不会将重复节点加入队列。

当$h=0$时，A*算法变为DFS；当$h=0$并且边权为$1$的时候变为BFS。

二、A*算法

A*算法找到的一条由图中节点以及边组成的路径。一般而言，A*算法基于BFS，同时也可以认为是对BFS搜索算法的优化。与之相对的IDA*则是基于DFS算法，对DFS算法的优化。

下面我们来分析A*算法的具体执行过程：

1.搜索区域(The Search Area)

我们以二维平面坐标系下的简单搜索为例进行分析。

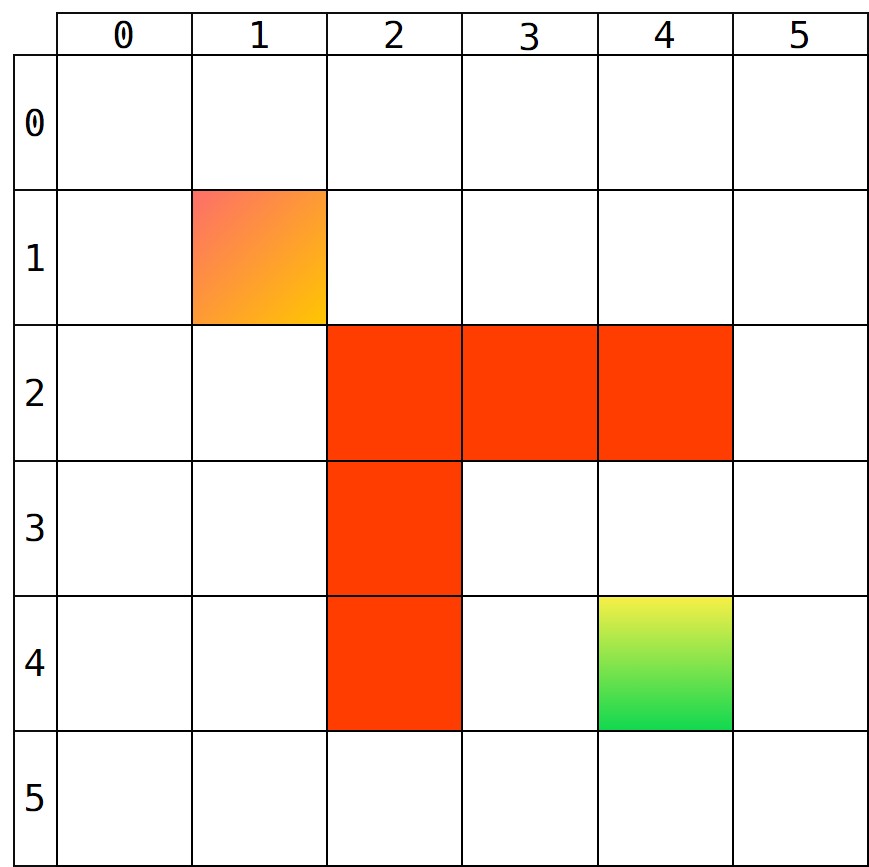
如图所示，两个渐变色点可以代表起点和终点，纯色方框代表不可经过的点，那么显然对于图中的区域被划分为了两种类型：

1. 可经过(Walkable)：包括正常路径、起点和终点，均属于可以经过的点
2. 不可经过(Unwalkable)：墙/禁止经过的点

在实际应用中，我们会遇到各种各样的图，可能有大量的图并能通过单纯的二维坐标系对点与点之间的关系(即边)进行描述。但无需担心：我们对于A*算法的表述是基于点进行的，如果换成其他边关的图也可以轻松的套用。

2.搜索起点(Search Starting)

经过对搜索区域的确定与划分，我们可以得到一组量化的结点。那么我们可以开始寻找最短路径。与普通搜索类似，A*算法以起点开始向四周检索相邻方格并进行扩展，直到扩展扫描到终点算法结束。

我们这样开始我们的寻路旅途：

1. 从起点 A 开始，并把它就加入到一个由方格组成的$open\_list$( 开放列表 ) 中。当然现在 $open\_list$ 里只有一项，它就是起点 A ，后面会慢慢加入更多的项。 $open\_list$ 里的格子是路径可能会是沿途经过的，也有可能不经过。基本上 $open\_list$ 是一个待检查的方格列表。
2. 查看与起点 A 相邻的方格 ( 忽略其中不可经过的方格 ) ，把其中可走的 ($walkable$) 或可到达的 ($reachable$) 方格也加入到 $openlist$ 中。把起点 A 设置为这些方格的父亲 ($parent\_node$ 或 $parent\_square$) 。当我们在追踪路径时，这些父节点的内容是很重要的。稍后解释。
3. 把 A 从 $open\_list$ 中移除，加入到 $close\_list$( 封闭列表 ) 中，$closelist$ 中的每个方格都是现在不需要再关注的。

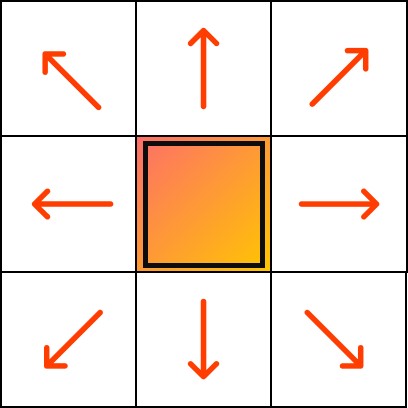
那么下一步，我么你需要从$ope{n}_{l}ist$中选一个与起点A相邻的方格，按下面描述的一样重复之前的步骤。但如果只是这样，那么这与普通的搜索没有区别了。所以正是对于路径的选择成为了A*不同于一般搜索的点，我们需要对邻接的点进行排序后选择合适的点。这里我们引入一个值$F$，这个值是确定组成路径方格的重点。

3.路径排序(Path Sorting)

我们提到了值$F$，那么这个值是如何得来的呢？

我们首先引入值$G$和$H$：

• $G$：从起点$A$按照生成的路径移动到指定方格的移动代价。对于$G$的值，我们有两种计算方式，对应平面上的两种距离计算方式：
  ①.欧拉距离：$(x_1-x_2{)}^2+(y_1-y_2{)}^2$
  ②.曼哈顿距离：$|x_1-x_2|+|y_1-y_2|$
  

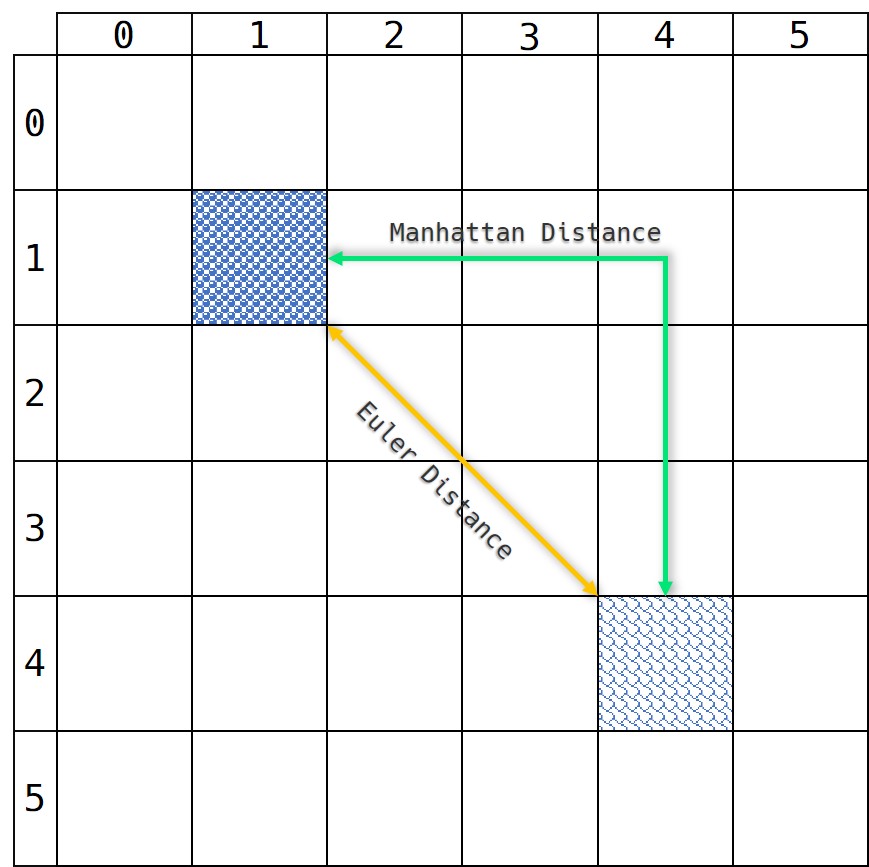
  由此我们可以得知，从一个方格向相邻的方格做纵向/横向移动时，$G$取$1$，当斜方向进行移动时，$G$取$\sqrt{2}$，那么在实际过程中，为了保证计算的简便性，我们将非整数取近似值并扩大$10$倍，即规定横纵向移动时代价为$10$，斜方向移动时消耗的代价为$14$.
  在对当前坐标进行计算时，找到当前坐标的父坐标然后判断移动方向，然后更新$F$的值即可。

• $H$：从指定方格移动到终点$B$的估算成本。对于该值的计算方法有许多种。
  我们主要使用$Manhattan$ 方法，也就是所谓的试探法。在试探法中，我们忽略掉路径中的障碍物，计算从当前方格横向或纵向移动到达目标所经过的方格数，忽略对角移动(直接计算当前点与目标点的曼哈顿距离)，然后把总数乘以 10 。
  需要注意的是，$H$值计算的是当前点到最终点的代价，而不是从父方格转移的代价，这是区别于$G$值的一点

那么可以根据$G$和$H$计算$F$：
$$F=G+H$$

4.寻路步骤总结

1. 从起点$S$开始，把$S$作为一个等待检查的方格，将其放入$open\_list$中。($open\_list$存放等待检查的方格的列表);

2. 寻找起点$S$周围可以到达的方格(最多八个)，并将它们加入$open\_list$，同时设置他们的父方格为$S$;

3. 从$open\_list$中删除起点$S$，同时将$S$加入$close\_list$($close\_list$用于存放不需要再进行检查的方格);

4. 计算每个周围方格的$F$值($F=G+H$);

5. 从$open\_list$中选取$F$值最小的方格$a$，并将其重$open\_list$中删除，放入$close\_list$中;

6. 继续检查$a$的临接方格：
   a). 忽略不可经过的方格以及被标记在$close\_list$中的方格，将剩余的方格加入$open\_list$，并计算这些方格的$F$值，同时设置父方格为$a$；
   b). 如果某邻接的方格$c$已经在$open\_list$中，则需计算新的路径从$S$到$c$的$G$值，判断是否需要更新：
   ·如果新的$G$值更小一些，则修改父方格为方格$a$，重新计算$F$值。注意：$H$值不需要改变，因为方格到达终点的预计消耗是固定的，不需要重复计算。
   ·如果新的$G$值更大一些，那么说明新路径不是一条更优的路径，则不需要更新值。

7. 继续从$open\_list$中找出$F$值最小的，跳跃至第5步继续循环执行。

8. 当$open\_list$出现终点$E$时，代表路径已经被找到，搜索成功

   如果$open\_list$为空，那么说明没有找到合适的路径，搜索失败

5.A*寻路算法分析

$Dijkstra$算法和A*都是最短路径问题的常用算法，下面就对这两种算法的特点进行一下比较。

1. $Dijkstra$算法计算源点到其他所有点的最短路径长度，A*关注点到点的最短路径(包括具体路径)。

2. $Dijkstra$算法建立在较为抽象的图论层面，A*算法可以更轻松地用在诸如游戏地图寻路中。

3. $Dijkstra$算法的实质是广度优先搜索，是一种发散式的搜索，所以空间复杂度和时间复杂度都比较高。

   对路径上的当前点，A*算法不但记录其到源点的代价，还计算当前点到目标点的期望代价，是一种启发式算法，也可以认为是一种深度优先的算法。

4. 由第一点，当目标点很多时，A*算法会带入大量重复数据和复杂的估价函数，所以如果不要求获得具体路径而只比较路径长度时，$Dijkstra$算法会成为更好的选择。

三、A*算法的应用

Sample.1 HDU-1043 Eight

Problem Description

The 15-puzzle has been around for over 100 years; even if you don’t know it by that name, you’ve seen it. It is constructed with 15 sliding tiles, each with a number from 1 to 15 on it, and all packed into a 4 by 4 frame with one tile missing. Let’s call the missing tile ‘x’; the object of the puzzle is to arrange the tiles so that they are ordered as:

 1  2  3  4
 5  6  7  8
 9 10 11 12
13 14 15  x

where the only legal operation is to exchange ‘x’ with one of the tiles with which it shares an edge. As an example, the following sequence of moves solves a slightly scrambled puzzle:

 1  2  3  4     1  2  3  4     1  2  3  4     1  2  3  4
 5  6  7  8     5  6  7  8     5  6  7  8     5  6  7  8
 9  x 10 12     9 10  x 12     9 10 11 12     9 10 11 12
13 14 11 15    13 14 11 15    13 14  x 15    13 14 15  x
            r->            d->            r->

The letters in the previous row indicate which neighbor of the ‘x’ tile is swapped with the ‘x’ tile at each step; legal values are ‘r’,‘l’,‘u’ and ‘d’, for right, left, up, and down, respectively.

Not all puzzles can be solved; in 1870, a man named Sam Loyd was famous for distributing an unsolvable version of the puzzle, and
frustrating many people. In fact, all you have to do to make a regular puzzle into an unsolvable one is to swap two tiles (not counting the missing ‘x’ tile, of course).

In this problem, you will write a program for solving the less well-known 8-puzzle, composed of tiles on a three by three arrangement.

Input

You will receive, several descriptions of configuration of the 8 puzzle. One description is just a list of the tiles in their initial positions, with the rows listed from top to bottom, and the tiles listed from left to right within a row, where the tiles are represented by numbers 1 to 8, plus ‘x’. For example, this puzzle

1 2 3
x 4 6
7 5 8

is described by this list:

1 2 3 x 4 6 7 5 8

Output

You will print to standard output either the word ``unsolvable’’, if the puzzle has no solution, or a string consisting entirely of the letters ‘r’, ‘l’, ‘u’ and ‘d’ that describes a series of moves that produce a solution. The string should include no spaces and start at the beginning of the line. Do not print a blank line between cases.

Analysis

首先分析题目大意：在 $3\times 3$ 的棋盘上，摆有八个棋子，每个棋子上标有 $1$ 至 $8$ 的某一数字。棋盘中留有一个空格，空格用 $X$ 来表示。空格周围的棋子可以移到空格中，这样原来的位置就会变成空格。给出一种初始布局和目标布局，找到一种从初始布局到目标布局最少步骤的移动方法。

此处的$H$可以认为是“不应该位于当前方格的数的个数”。那么很容易写出A*算法解决这道题。

我们首先来做这道题的简化版：洛谷[P1379] 八数码难题

题目链接：P1379 八数码难题 - 洛谷

我们首先构造本题目的数据结构(BFS队列中储存的数据结构)，一个矩阵储存状态，一个整数变量储存步数。

对于本题目，显然$H$函数要求的是不应该位于当前方格的数字的个数，那么我们可以根据这个目的编写一个$H$函数；

然后我们从头开始匹配矩阵，每次对一个点的周围的点进行判断、交换和入队，这里采用优先队列并重载比较运算符，定义优先级为$step+h(x)$大的优先。

#include <bits/stdc++.h>
using namespace std;

const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, 1, -1};
int fx = 0, fy = 0;

struct matrix{
    int a[5][5];
    bool operator<(matrix x) const{
        for(int i = 1; i <= 3; i++)
            for(int j = 1; j <= 3; j++)
                if(a[i][j] != x.a[i][j]) return a[i][j] < x.a[i][j];
        return false;
    }        
}f, st;

inline int h(matrix a){
    int ans = 0;
    for(register int i = 1; i <= 3; i++)
        for(register int j = 1; j <= 3; j++)
            if(a.a[i][j] != st.a[i][j]) ans++;
    return ans;    
}

struct node{
    matrix a;
    int t;
    bool operator<(node x) const { return t + h(a) > x.t + h(x. a); }
}x;

inline void init(){
    st.a[1][1] = 1, st.a[1][2] = 2, st.a[1][3] = 3;
    st.a[2][1] = 8, st.a[2][2] = 0, st.a[2][3] = 4;
    st.a[3][1] = 7, st.a[3][2] = 6, st.a[3][3] = 5;
}

priority_queue<node> q;
set<matrix> s;
signed main(){
    init();
    for(register int i = 1; i <= 3; i++){
        for(register int j = 1; j <= 3; j++){
            char tmp; scanf("%c", &tmp);
            f.a[i][j] = tmp - '0';
        }
    }
    q.push({f, 0});
    while(!q.empty()){
        x = q.top(); q.pop();
        if(!h(x.a)) return printf("%dn",  x.t), 0;
        for(int i = 1; i <= 3; i++)
            for(int j = 1; j <= 3; j++) 
                if(!x.a.a[i][j]) fx = i, fy = j;
        for(int i = 0; i < 4; i++){
            int nx = fx + dx[i], ny = fy + dy[i];
            if(nx > 0 && nx <= 3 && ny > 0 && ny <= 3){
                swap(x.a.a[fx][fy], x.a.a[nx][ny]);
                if(!s.count(x.a)) s.insert(x.a), q.push({x.a, x.t + 1});
                swap(x.a.a[fx][fy], x.a.a[nx][ny]);
            }
        }
    }
    return 0;
}

有了简化版的理解，这道题目就没有那么难了，可以继续根据以上思路类比写出代码。

#include<iostream>
#include<vector>
#include<queue>
#include<string>
#include<unordered_map>
#define _for(i, a, b) for (int i = (a); i < (b); ++i)
#define _rep(i, a, b) for (int i = (a); i <= (b); ++i)
#define FOR(i, a, b) for (int i = (a); i >= (b); --i)
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> IntVec;

const int N = 1000 + 10;
string s(9, 0), END = "12345678x";
unordered_map<string, string> vis;
int dx[] = { -1, 1, 0, 0}, dy[] = {0, 0 ,-1, 1 };
char dir[] = { "durl" };

void bfs(){
	queue<string> q;
	q.push(END);

	while(!q.empty()){
		string t = q.front();
		q.pop();

		int u = t.find('x');
		int x = u / 3, y = u % 3;
		string dist = vis[t];
		
		_for (i, 0, 4){
			int a = x + dx[i], b = y + dy[i];
			if (0 <= a && a < 3 && 0 <= b && b < 3){
				swap(t[u], t[a * 3 + b]);
				if (!vis.count(t)){
					vis[t] = dist + dir[i];
					q.push(t);
				}
				swap(t[u], t[a * 3 + b]);
			}
		}
	}
}

int main(){
#ifdef LOCAL
	freopen("data.in", "r", stdin);
#endif
	ios::sync_with_stdio(false), cin.tie(0), cin.tie(0);
	bfs();
	while(cin>> s[0]){
		_for(i, 1, 9) cin >> s[i];
		if (vis.count(s)){
			string ans = vis[s];
			reverse(ans.begin(), ans.end());
			cout << ans << endl;
		}
		else puts("unsolvable");
	}
	return 0;
}

最后

以上就是贪玩蜡烛为你收集整理的A*算法 详解与例题的全部内容，希望文章能够帮你解决A*算法 详解与例题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。