leetcode之动态规划

核心就两步：

（1）确定dp[i]的含义

（2）写出状态转移方程

另外还要注意两点：

然后还要初始化dp数组一些位置的值，比如dp[0]和dp[1],因为递推的时候是需要先知道一些值才能推出另一些值

决定开多大数组的时候，可以想一下你要返回的是什么，根据这个推导出数组的长度，比如你要返回dp[n],那么数组的长度肯定是n+1，如果只开大小为n的数组，那dp[n]就越界了

1.以爬楼梯问题为例，总结动态规划的步骤：

第一步：定义dp数组（可能时一维数组，也可能是二维数组），这一步需要确定两个问题：

（1）dp[i]或者dp[i][j]是什么含义（比如在爬楼梯问题中，dp[i]表示到达第i层有多少种爬法）

（2）到底开多大的空间，你搞懂了第一个问题dp[i]或者dp[i][j]是什么含义，就知道到底要开多大的空间了，由于在爬楼梯问题中，dp[i]表示到达第i层有多少种爬法，你最后求的是到达第n层所需要的爬法数，所以最后要返回的是dp[n]，所以显然要开n+1大小的数组，这样才能有dp[n](如果你只开n大小的数组，那么最后只能返回dp[n-1]）

第二步：初始化这个数组中的部分值

dp[0]题目已经给了等于1

dp[1]就是到达第一层有几种爬法，显然dp[1]=1

第三步：/写出状态转移方程确定dp数组中其他位置元素的值

class Solution 
{
    public int minCostClimbingStairs(int[] cost) 
    {
       
       //dp[i]表示到达第i级楼梯所需的最小代价，台阶的编号从0开始
       //比如总共有7级台阶，0号，1号，2号...6号，cost数组就是第0阶，第1阶，第2阶...第5阶向上爬的费用的，最后返回dp[6],所以dp数组长度是cost数组的长度+1
       int[] dp=new int [cost.length+1];

       //由于可以选择从0或者1号台阶出发，所以到达第0级台阶或者第一级台阶的花费为0
       dp[0]=0;
       dp[1]=0;
       for(int i=2;i<dp.length;i++)
       {
          dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
       }
       return dp[dp.length-1];     
    }
}

力扣509  斐波那契数列

class Solution {
    public int fib(int n) {

        if(n==0)  return  0;
        if(n==1)  return   1;
                          
        int[]  dp=new int[n+1];

        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
}

下面两道题青蛙跳台阶和爬楼梯是一样的题目

爬楼梯问题：爬到第n层有可能是从第n-1层然后跨一层到达第n层的，也可能时从第n-2层然后跨两层到达第n层的dp[i]=dp[i-1]+dp[i-2]

青蛙跳台阶：力扣

 leetcode70爬楼梯：力扣     dp[i]表示到达第i层有多少种爬法

class Solution 
{
    public int numWays(int n) 
    {
        if (n == 0) return 1;
        if (n == 1) return 1;

        //定义一个dp数组，dp[i]表示到达第i层有多少种爬法
        int[] dp = new int[n + 1];

        //初始化dp数组
        dp[0] = 1;
        dp[1] = 1;

        //写出状态转移方程确定数组中其他位置元素的值
        for (int i = 2; i <= n; i++) 
        {
            dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
        }
        return dp[n];
    }
}

力扣746 使用最小花费爬楼梯

 dp[i]表示到达第i级楼梯所需的最小代价

状态转移方程：有可能跨越一个台阶上来的，也有可能是跨越两个台阶上来的

所以状态转移方程：dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])注意传入的cost数组里面元素个数等于台阶数-1。因为最高台阶是没有代价的

2.连续子数组的最大和        力扣53

比如数组为：1，-2，3，10，-4，7，2，-5

以1结尾的所有子数组，以-2结尾的所有子数组，以3结尾的所有子数组.........以7结尾的所有子数组，以2结尾的所有子数组，以-5结尾的所有子数组

开一个数组dp[nums.length],

dp[i]表示以nums[i]结尾的连续子数组的最大和

比如：dp[0]表示以nums[0](也就是1）结尾的所有子数组中最大和，显然dp[0]=1

dp[1]表示以nums[1]（也就是-2）结尾的所有子数组中最大和，显然dp[1]=-1

.......

显然dp[i+1]=max(nums[i+1],dp[i]+nums[i+1])

也就是说，dp[i+1]要么就是（1)等于dp[i]加上nums[i+1]，即前面的子序列+当前位置这个数

（2）要么就是不要前面的子序列，只要nums[i+1]这个数（nums[i]这个数一定要有，因为是以这个数结尾的连续子数组）

其实到底要不要前面的子数组dp[i]，就看它是不是大于0的，大于0肯定就要，是负数就不要

class Solution 
{
    public int maxSubArray(int[] nums) 
    {
        int[] dp=new int[nums.length];
        dp[0]=nums[0];
        for(int i=0;i<nums.length-1;i++)
        {
            dp[i+1]=Math.max(nums[i+1],dp[i]+nums[i+1]);
        }
        
        //对dp数组进行排序，找出最大值，最大值就是排序后的最后一个值
        Arrays.sort(dp);
        return dp[nums.length-1];
    }
}

如果题目要求你打印出这个 最大和连续子数组，dp[i]表示以nums[i]结尾的连续子数组的最大和

所以找出这个最大值，然后从后往前加，一直加到最大和为止

class Solution 
{
    public int[] maxSubArray(int[] nums) 
    {
        int[] dp=new int[nums.length];
        dp[0]=nums[0];
        for(int i=0;i<nums.length-1;i++)
        {
            dp[i+1]=Math.max(nums[i+1],dp[i]+nums[i+1]);
        }
        
        //对dp数组进行排序，找出最大值，最大值就是排序后的最后一个值
        Arrays.sort(dp);

        int  max=dp[nums.length-1];
        ArrayList result=new ArrayList();
        int sum=0; 

        for(int i=0;i<dp.length;i++)
        {
           if(dp[i]==max)
           {
              for(int j=i;j>0;j--)
              {
                 result.add(nums[j])
                 sum=sum+num[j];
                 if(sum==max)
                 {
                   result.reverse();
                   int[]  temp=new  int[result.size()];
                   for(int k=0;k<result.size();k++)
                   {
                     temp[k]=result.get(k);
                   }
                   return  temp;
                 }
              }
           }

        }
    }
}

3.用动态规划来创建前缀和数组

力扣303

class NumArray 
{
    //定义一个数组，这个数组是前缀和数组，也就是说presum[i]表示前i个数的和
    //也就是从nums[0]到nums[i]所有数之和

    int[]  presum;
    public NumArray(int[] nums)
    {
        //这里不接收nums数组，而是根据nums数组求出前缀和数组

        presum=new int[nums.length];
        //初始化
        presum[0]=nums[0];

        for(int i=0;i<nums.length-1;i++)
        {
            presum[i+1]=presum[i]+nums[i+1];
        }

    }
    
    public int sumRange(int left, int right)
    {
      if(left==0)
      {
          return presum[right];
      }
      return  presum[right]-presum[left-1];
    }
}

4.力扣55 跳跃游戏

从后往前，把数组填完

class Solution
{
    public boolean canJump(int[] nums)
    {
       //开一个数组，dp[i]代表nums[i]这个位置能否跳到最后一个下标
       boolean[]  dp=new  boolean[nums.length]; 

       dp[nums.length-1]=true;

       for(int i=nums.length-2;i>=0;i--)
       {
         //dp[i]=false;

         //遍历dp[i]后面的nums[i]个数,nums[i]表示第i个台阶最多可以前进nums[i]个位置
         //只要第i级台阶能跳到的台阶中，有一个台阶能跳到最后一级台阶，那第i级台阶就一定能跳到最后一级台阶
        //遍历第i级台阶能跳到的台阶，dp[i+1],dp[i+2]....dp[i+nums[i]],有一个能跳到，dp[i]就能跳到
         for(int j=1;j<=nums[i];j++)
         {
             if(dp[i+j]==true)
             {
                 dp[i]=true;
                 break;
             }
         }
       }
       return dp[0];
    }
}

5.力扣198 打家劫舍

其实概括一下就是不能偷连续两家

dp[i][0]表示0~i个房屋，而且不偷第i个屋，获得的最高金额
dp[i][1]表示0~i个房屋，而且偷第i个屋，获得的最高金额

状态转移方程：dp[i]和dp[i-1]之间的关系

class Solution 
{
    public int rob(int[] nums) 
    {
        int[][] dp=new int[nums.length][2];
        //dp[i][0]表示0~i个房屋，而且不偷第i个屋，获得的最高金额
        //dp[i][1]表示0~i个房屋，而且偷第i个屋，获得的最高金额

        dp[0][0]=0;
        dp[0][1]=nums[0];

        for(int i=1;i<nums.length;i++)
        {
           //第i个房屋不偷，所以前一个房屋偷不偷都可以
           dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]);

           //如果第i个房屋偷，那前一个房屋不能偷
           dp[i][1]=dp[i-1][0]+nums[i];
        }
        
        //最后一个房子只有偷还是不偷两种可能
        return Math.max(dp[nums.length-1][0],dp[nums.length-1][1]);
    }
}

力扣213 打家劫舍||d

打家劫舍里面nums数组是nums[0]~nums[n-1]

就是将打家劫舍|里面的nums数组替换成nums[0]~nums[n-2]和nums[1]~nums[n-1],进行两次打家劫舍|

1.偷第一个房子，不偷最后一个房子，即只考虑nums[0]~倒数第二个元素的情况下的最大金额p1

2.不偷第一个房子，偷最后一个房子，即只考虑nums[1]~倒数第一个元素的情况下的最大金额p2

Math.max(p1,p2)即可

也就是打家劫舍2其实就是做两次打家劫舍1,然后求更大值即可

class Solution 
{
    public int rob(int[] nums) 
    {
        if(nums.length==0)  return 0;
        if(nums.length==1)  return nums[0];
        int[] nums1=Arrays.copyOfRange(nums, 0, nums.length - 1);
        int[] nums2=Arrays.copyOfRange(nums, 1, nums.length);
        int num1=help(nums1);
        int num2=help(nums2);
        return Math.max(num1,num2);
    }    
    public int help(int[] nums)
    {
        int[][] dp=new int[nums.length][2];
        //dp[i][0]表示0~i个房屋，而且不偷第i个屋，获得的最高金额
        //dp[i][1]表示0~i个房屋，而且偷第i个屋，获得的最高金额

        dp[0][0]=0;
        dp[0][1]=nums[0];

        for(int i=1;i<nums.length;i++)
        {
           //第i个房屋不偷，所以前一个房屋偷不偷都可以
           dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]);
           //如果第i个房屋偷，那前一个房屋不能偷
           dp[i][1]=dp[i-1][0]+nums[i];
        }
        return Math.max(dp[nums.length-1][0],dp[nums.length-1][1]);
    }    
}

6.不同路径

力扣62

dp[i][j]表示从（0，0)处到（i,j)这个位置有多少种不同的路径

状态转移方程：    dp[i][j]=dp[i-1][j]+dp[i][j-1];

到(i，j)这个位置要么上一步从（i-1，j）位置向下走一步，要么上一步从（i，j-1）位置向右走一步
           

class Solution 
{
    public int uniquePaths(int m, int n) 
    {
        int[][] dp=new int[m][n];
        //dp[i][j]表示从（0，0)处到（i,j)这个位置有多少种不同的路径

        dp[0][0]=1;

        //由于只能向下走或者是向右走一步
        //所以dp[i][0]也就是第一列，还有dp[0][j]也就是第一列都只有1种走法
        
        //第一列全部置为1
        for(int i=0;i<m;i++)
        {
            dp[i][0]=1;
        }
        //第一行全部置为1
        for(int j=0;j<n;j++)
        {
            dp[0][j]=1;
        }
        //现在根据状态转移方程填上除了第一行第一列的其他位置
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
             //到（i，j）这个位置要么上一步从（i-1，j）位置向下走一步，要么上一步从（i，j-1）位置向右走一步
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

64. 最小路径和 - 力扣（LeetCode）leetcode64  最小路径和

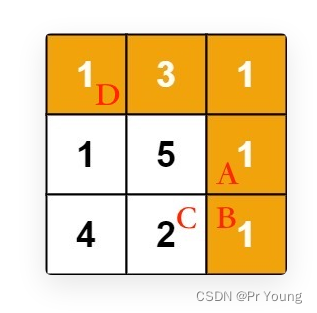
比如希望从D走到B，最后一步有两种情况（1）从A走到B  （2）从C走到B

从D走到A的最小路径和为6，从D走到C的最小路径和为8

由于6<8,所以从D走到B的最小路径和是先从D走到A，然后再从A走到B

dp[i][j]的意思是从nums[0][0]到nums[i][j]的最小路径和

状态转移方程：dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+nums[i][j]； 只能从左边或者上面走过来

class Solution 
{
    public int minPathSum(int[][] nums) 
    {
        //m*n的矩阵
        int m=nums.length;
        int n=nums[0].length;

        //dp[i][j]的意思是从nums[0][0]到nums[i][j]的最小路径和
        int[][] dp=new int[m][n];

        dp[0][0]=nums[0][0];

        for(int i=1;i<m;i++)
        {
            //由于只能往右走或者往下走，所以第一列的位置只能从上一行来
            dp[i][0]=dp[i-1][0]+nums[i][0];
        }

        for(int j=1;j<n;j++)
        {
            //由于只能往右走或者往下走，所以第一行的位置只能从左边的一列来
            dp[0][j]=dp[0][j-1]+nums[0][j];
        }

        for(int i=1;i<m;i++)
        {
          for(int j=1;j<n;j++)
          {
            //d[i][j]的上一行元素是d[i-1][j](列值相同)
            //d[i][j]的左边一列元素是d[i][j-1](行值相同)
            dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+nums[i][j];
          }   
        }
        return dp[m-1][n-1];
    }
}

力扣剑指offer47 礼物的最大价值

和上面的最小路径和刚好相反，相当于求最大路径

只要改一行代码即可

dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+nums[i][j];

改成：

 dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])+nums[i][j];

 63  不同路径||

与1相比只是多了障碍物，在代码上唯一不同的地方在于：初始化第一行和第一列的时候，如果这个位置有障碍物，那么dp[0][i]或者dp[i][0]就都等于0，也就是没有路径可达，其他代码是一样的

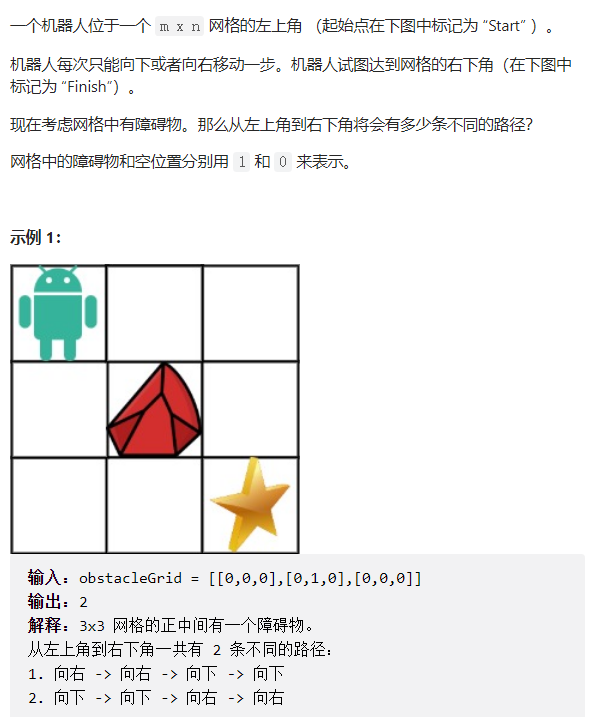
 与1相比只是多了障碍物，在代码上唯一不同的地方在于：初始化第一行和第一列的时候，如果这个位置有障碍物，那么这个位置以及这个位置往后的位置dp[0][i]或者dp[i][0]都等于0，也就是没有路径可达，其他代码是一样的

class Solution {
    public int uniquePathsWithObstacles(int[][] nums) {
        int m=nums.length;
        int n=nums[0].length;
        
        int[][] dp=new int[m][n];
         if(nums[0][0]==1)   return 0;

         dp[0][0]=1;

        //填第一行
        for(int i=1;i<n;i++)
        {
            if(nums[0][i]==1)
            {
                dp[0][i]=0;//这一行其实可以不写，默认这个位置就是0
                break;//这个位置以及这个位置后面的位置都是0
            }
            dp[0][i]=1;
        }

        //填第一列
        for(int j=1;j<m;j++)
        {
            if(nums[j][0]==1)
            {
                dp[j][0]=0;//这一行其实可以不写，默认这个位置就是0
                break;//这个位置以及这个位置后面的位置都是0
            }
            dp[j][0]=1;
        }

        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                if(nums[i][j]==1)  dp[i][j]=0;
                else
                {
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];   
                }
            }
                
        }
        return  dp[m-1][n-1];
    }
}

leetcode72  编辑距离 

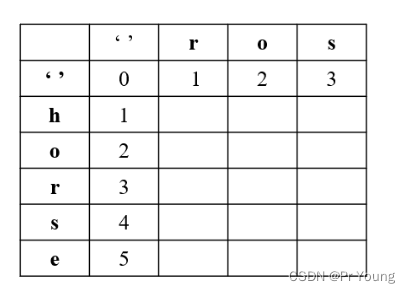
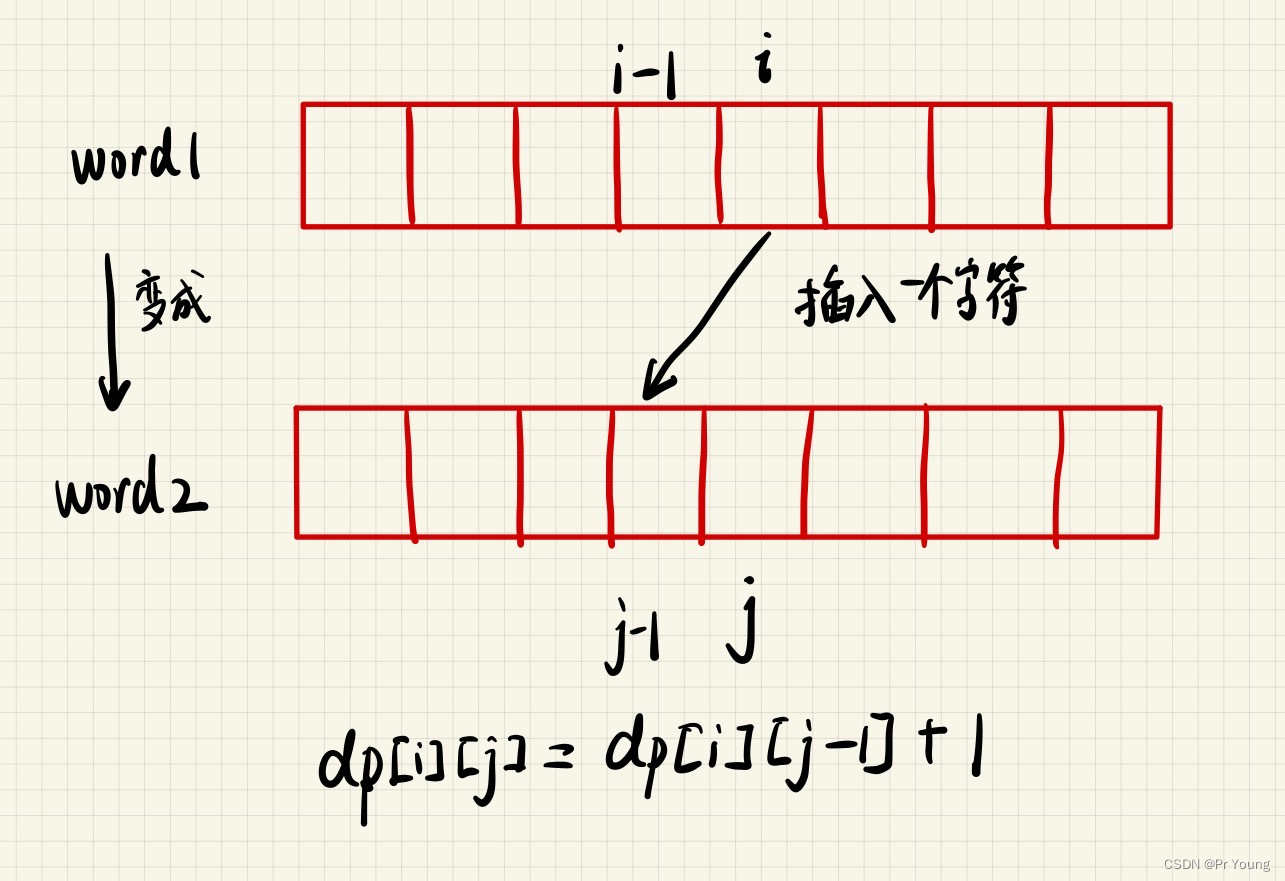
 dp[i][j]表示word1的前i个字母转换成word2的前j个字母所使用的最少操作,最终返回的是dp[length1][length2]

 

 

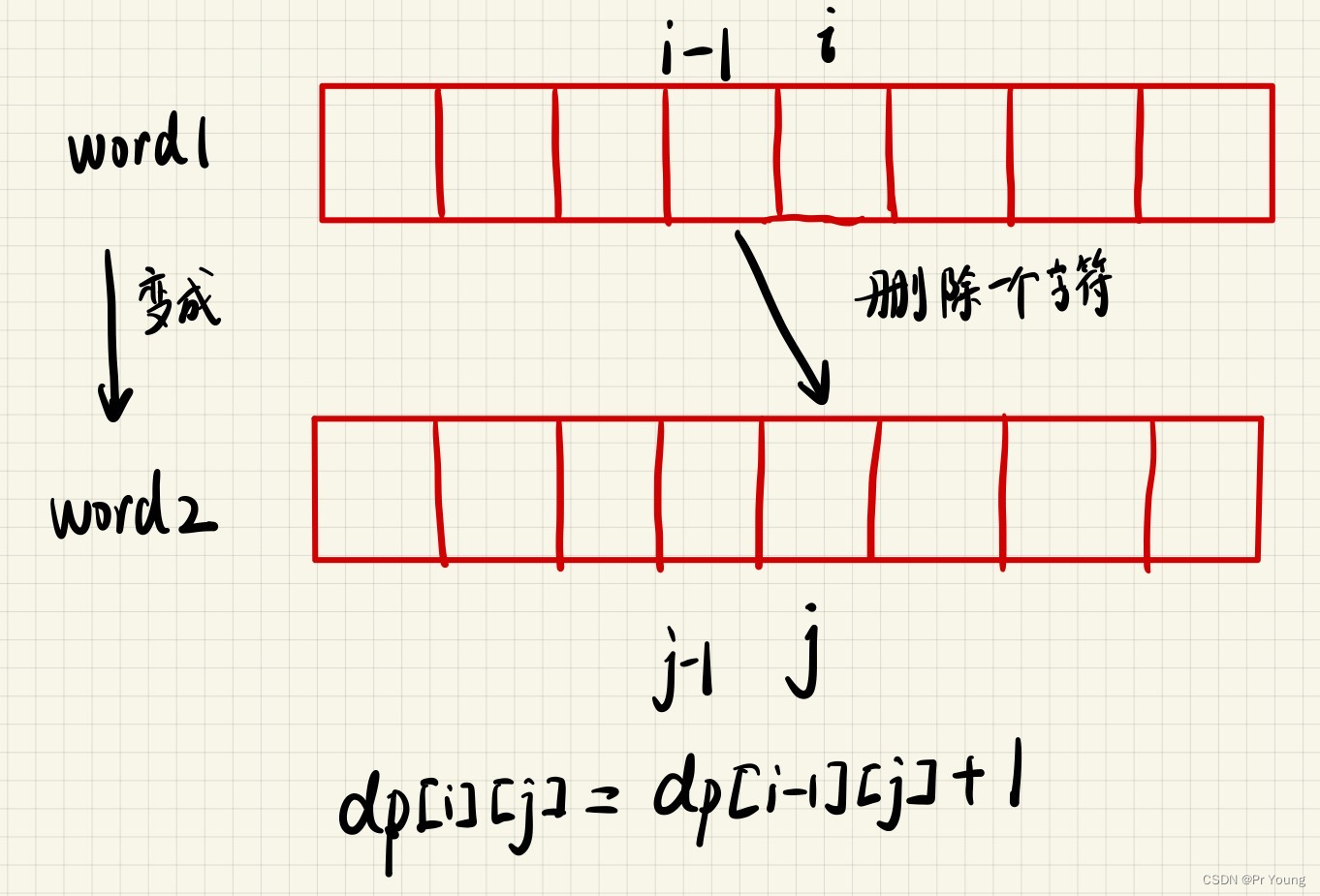
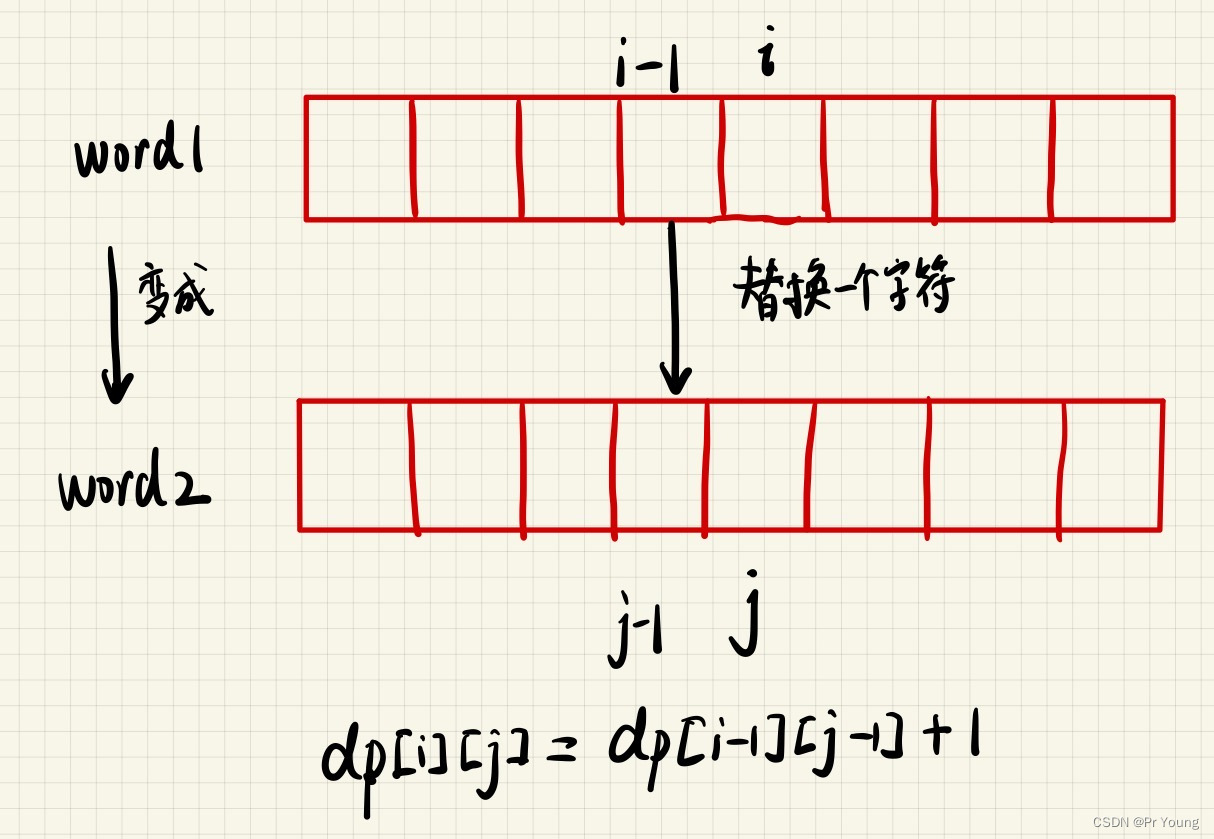
class Solution 
{
    public int minDistance(String word1, String word2)
    {
        //word1转化成word2
        
        
        int length1=word1.length();
        int length2=word2.length();

        //dp[i][j]表示word1的前i个字母转换成word2的前j个字母所使用的最少操作,最终返回的是dp[length1][length2]
        int[][] dp=new int[length1+1][length2+1];

        for(int i=0;i<=length1;i++)
        {
            //word1的前i个字母转换成word2的前0个字母，显然需要的最少操作数就是i(i个字母全部删除)
            dp[i][0]=i;
        }

        for(int j=0;j<=length2;j++)
        {
            //word1中的前0个字母转换成前j个字母，显然需要的最少的操作数就是j(插入j个字符)
            dp[0][j]=j;
        }

        for(int i=1;i<=length1;i++)
        {
            for(int j=1;j<=length2;j++)
            {
                //如果当前的字母相同，则dp[i][j] = dp[i - 1][j - 1]，否则取增加，删除，替换三个操作的最小值
                if(word1.charAt(i-1)==word2.charAt(j-1))
                {
                    dp[i][j]=dp[i-1][j-1];
                }
                else
                {
                    //Math.min只能求两个数中更小的那一个,所以三个数求最小值需要用两次Math.min
                    //dp[i-1][j-1]+1表示替换一个字符
                    //dp[i-1][j]+1表示删除一个字符
                    //dp[i][j-1]+1表示插入一个字符
                    dp[i][j]=1+Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i][j-1]);
                }
            }
        }
        return dp[length1][length2];
    }
}

力扣279  完全平方数

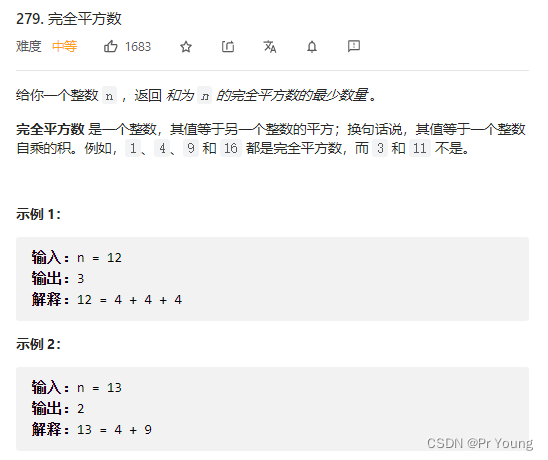
也就是说求n最少可以表示成几个完全平方数之和，最多肯定是n个（拆成n个1之和）

关键是列举比n小的完全平方数，比如比21小的完全平方数有1，4，9，16

状态转移方程：dp[21]=Math.min（1+dp[21-1*1],1+dp[21-2*2],1+dp[21-3*3],1+dp[21-4*4]）

=Math.min（1+dp[20],1+dp[17],1+dp[12],1+dp[5]）

同理如果是求dp[72]

dp[72]=Math.min（1+dp[72-1*1],1+dp[72-2*2],1+dp[72-3*3],1+dp[72-4*4],1+dp[72-5*5）,1+dp[72-6*6],1+dp[72-7*7],,1+dp[72-8*8])

dp[n]=Math.min（1+dp[n-1*1],1+dp[n-2*2],1+dp[n-3*3],1+dp[n-4*4]...........,1+dp[i-j*j])

j*j是小于n的最大完全平方数

class Solution
{
    public int numSquares(int n)
    {
        //求正整数n最少可以表示为几个完全平方数之和

        //dp[i]表示正整数i最少可以表示为几个完全平方数之和

        int[]  dp=new int[n+1];

        Arrays.fill(dp,Integer.MAX_VALUE);
        
        dp[0]=0;

        for(int i=1;i<=n;i++)
        {
            for(int j=1;j*j<=i;j++)
            {
                dp[i]=Math.min(dp[i],1+dp[i-j*j]);
            }
        }
        return  dp[n];
    }
}

力扣221 最大正方形

dp[i][j]的含义是以matrix[i]为右下角的正方形的最大边长

状态转移方程：dp[i][j]=Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]))+1;

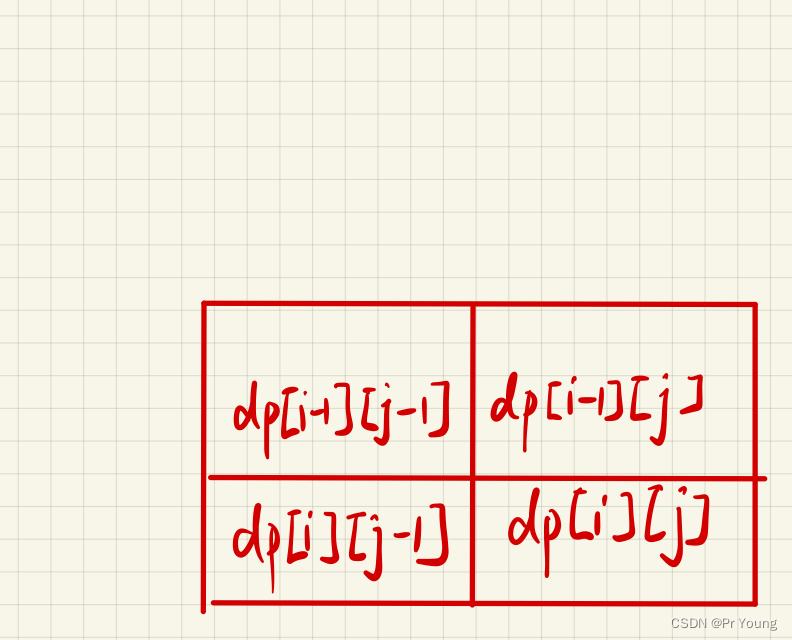
class Solution
{
    public int maximalSquare(char[][] matrix)
    {
        int m=matrix.length;
        int n=matrix[0].length;

        //dp[i][j]的含义是以matrix[i]为右下角的正方形的最大边长
        int[][]  dp=new int[m][n];

        int  max=0;

        //初始化dp数组第一列
        for(int i=0;i<m;i++)
        {
            if(matrix[i][0]=='1')
            {
                dp[i][0]=1;
                max=1;
            }
        }

        //初始化dp数组第一行
        for(int i=0;i<n;i++)
        {
            if(matrix[0][i]=='1')
            {
                dp[0][i]=1;
                max=1;
            }
        }

        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                if(matrix[i][j]=='1')
                {
                    dp[i][j]=Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]))+1;
                    max=Math.max(dp[i][j],max);
                }
            }
        }
        return  max*max;
    }
}

139 单词拆分

这是一个完全背包问题，

class Solution 
{
    public boolean wordBreak(String target, List<String> wordDict)
    {
        //利用字符列表的单词是否可以拼出字符串s

        //dp[i]表示：target字符串中前i个字符组成的字符串能否由字典里的单词拼接成,i=1,2,3.....
        boolean[]  dp=new  boolean[target.length()+1];

        dp[0]=true;

        //开始填满dp数组
        for(int i=1;i<dp.length;i++)
        { 
            for(int j=0;j<i;j++)
            {
                if(dp[j]==true&&wordDict.contains(target.substring(j,i)))
                {
                  dp[i]=true;
                }
            }
        }

        return  dp[target.length()];
    }
}

力扣674   最长连续递增序列

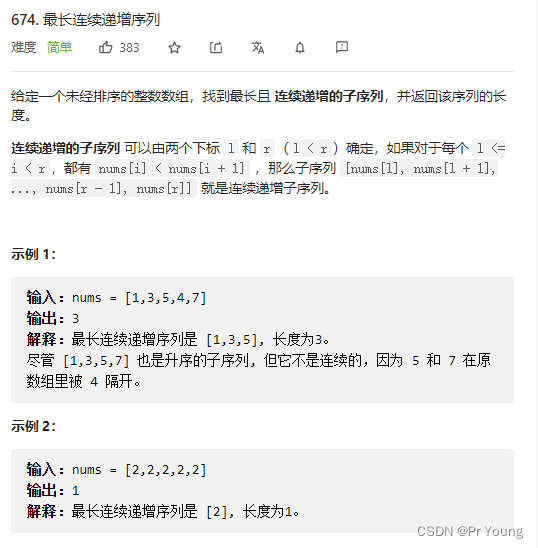
 其实这道题不用动态规划也可以做，就是用一个指针遍历，一直滑呀滑呀滑，滑到不递增为止，继续重新开始滑

 dp[i]表示以nums[i]结尾的连续序列的最长长度（这个值最小是1）

核心代码：如果当前元素，比前一个元素大，那当前元素的dp[i]就比前一个元素的dp[i-1]要大1

           if(nums[i]>nums[i-1])
           {
               dp[i]=dp[i-1]+1;
           }

class Solution 
{
    public int findLengthOfLCIS(int[] nums) 
    {
        int[]  dp=new  int[nums.length];

        Arrays.fill(dp,1);

        int max=1;

        for(int i=1;i<nums.length;i++)
        {
           if(nums[i]>nums[i-1])
           {
               dp[i]=dp[i-1]+1;
           }
           max=Math.max(max,dp[i]);
        }
        
        return  max;
    }
}

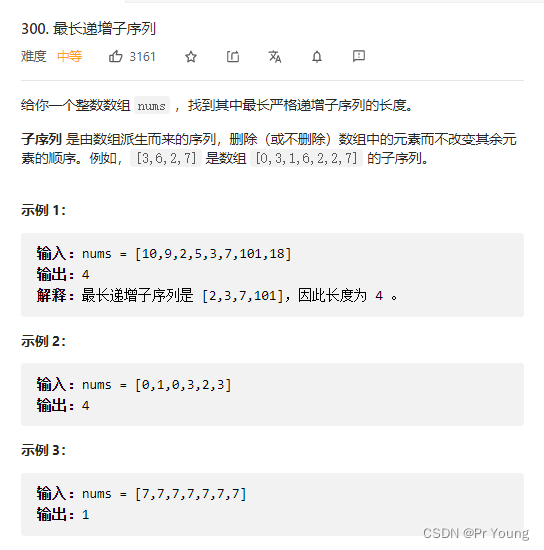
力扣300  最长递增序列  不要求连续了，所以求dp[i]需要遍历nums[i]之前的每一个元素的dp[j]，求出dp[j]中最大的

class Solution
{
    public int lengthOfLIS(int[] nums) 
    {
       //dp[i]表示以nums[i]结尾的最长递增子序列的长度
        int[] dp=new int[nums.length];

       // 初始化，所有位置先置为1，因为不管以什么结尾，起码自己本身的长度就是1
        Arrays.fill(dp,1);

        int result=1;

        for(int i=0;i<nums.length;i++)
        {
            //对于每一个位置，都要遍历前面的每个位置，前面比当前小的数中dp[i]最大的dp[i]加1，就是当前dp[i]
            int temp=0;
            for(int j=0;j<i;j++)
            {
                if(nums[j]<nums[i])
                {
                  //求出比当前数更小的数中，dp[i]最大的那个dp[i]
                  temp=Math.max(temp,dp[j]);               
                }
            }
            dp[i]=temp+1;
            //所有dp[i]中，最大的那个dp[i]就是我们要返回的结果
            result=Math.max(result,dp[i]);
        }
        return result;
    }
}

7.322. 零钱兑换 - 力扣（LeetCode）

 假设coins数组为[1,2,5,7,10],即面额为1，2，5，7，10

dp[0]=0

dp[1]=1

dp[2]=1

 dp[3]=dp[1]+两张1元的，或者是dp[3]=dp[2]+1张1元的

 所以dp[3]=Math.min(dp[1]+2,dp[2]+1)=2

 dp[4]=dp[3]+1张1元的，或者dp[2]+1张两元的，dp[4]=Math.min(dp[3]+1,dp[2]+1)=2

  .....

最后dp[14]=dp[13]+1张1元的,或者是dp[12]+1张2元的,或者dp[7]+1张7元的，或者dp[4]+1张10元

dp[14]=Math.min(dp[13]+1,dp[12]+1,dp[7]+1,dp[4]+1)

核心就是一句话：

remain_money=总金额-硬币的面值   这个数   能否被拼凑出来

如果这个数能被拼凑出来：

那拼凑总金额所需要的硬币数=dp[remain_money]+1

拼凑总金额所需要的最少硬币数=Math.min(dp[remain_money1]+1,dp[remain_money2]+1......)

class Solution 
{
    public int coinChange(int[] coins, int amount) 
    {
        //最后要拼出总金额amout
        int[] dp=new int[amount+1];
        //dp[i]的含义是;组成总金额i需要的最少钞票数量
        
        //数组初始化，所有位置填-1
        Arrays.fill(dp,Integer.MAX_VALUE);

        dp[0]=0;

        //依次求出dp[1],dp[2]......dp[amount]
        for(int i=1;i<=amount;i++)
        {
            //对于每个总金额i，遍历面值数组coins
            for(int j=0;j<coins.length;j++)
            {
              //总金额减去面值,如果dp[remain]不为-1，说明可以拼成总金额remain，那么就有dp[i]=dp[remain]+1(加1张表示加上1张已存在的面值)
              int remain_money=i-coins[j];
              
              //总金额比最小的面值还小(比如面值为2，5，10  现在轮到面值为10，总金额为8)，那就下一轮面值（注意面值数组不一定是单调递增的）
              if(remain_money<0)  continue;

              //如果剩下的钱拼不出来，直接下一轮面值
              if(dp[remain_money]==Integer.MAX_VALUE)  continue;
 
              //如果剩下的钱可以拼出来
              if(dp[remain_money]!=Integer.MAX_VALUE)
              {
                  dp[i]=Math.min(dp[i],dp[remain_money]+1);
              } 
            }          
        }
        if(dp[amount]==Integer.MAX_VALUE)  return -1;
        return  dp[amount];
    }
}

8.377组合总和IV   

 这个其实就是变形版的爬楼梯问题：对于每一集级台阶可以往上前进nums[0]或者nums[1]......nums[n-1]个台阶

也就是说数组中每个元素都是能够前进的台阶数，target就是最终希望能够到第几级台阶

状态转移方程：dp[i]=dp[i-nums[0]]+dp[i-nums[1]]]+.......+dp[i-nums[n-1]],到达第i个台阶，

可以从i-nums[0]级台阶上来，也可以从i-nums[1]级台阶上来........

class Solution {
    public int combinationSum4(int[] nums, int target) {
        
      //dp[i]表示有多少种方式到第i级台阶
      int[] dp=new int[target+1];

      dp[0]=1;
      for(int i=1;i<=target;i++)
      {
          for(int num:nums)
          {
              if(i-num>=0)
              {
                 dp[i]=dp[i-num]+dp[i];
              }
          }
          
      }
      return dp[target];
    }
}

最后

以上就是等待舞蹈为你收集整理的leetcode之动态规划的全部内容，希望文章能够帮你解决leetcode之动态规划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。