matlab qpsk 星座图,QPSK误码率和星座图MATLAB仿真

一、数字调制就是把数字基带信号的频谱搬移到高频处，形成适合在信道中传输的带通信号。基本的数字调制方式有振幅键控(ASK)、频移键控(FSK)、绝对相移键控(PSK)、相对(差分)相移键控(DPSK)。在接收端可以采用想干解调或非相干解调还原数字基带信号。

数字信号的传输方式分为基带传输和带通传输。然而，实际中的大多数信道(如)无线信道具有丰富的低频分量。为了使数字信号在带通信道中传输，必须用数字基带信号对载波进行调制，以使信号与信道的特性相匹配。

通信系统的抗噪声性能是指系统克服加性噪声影响的能力。在数字通信系统中，信道噪声有可能使传输码元产生错误，错误程度通常用误码率来衡量。因此，与分析数字基带系统的抗噪声性能一样，分析数字调制系统的抗噪声性能，也就是求系统在信道噪声干扰下的总误码率。

误码率(BER：bit error ratio)是衡量数据在规定时间内数据传输精确性的指标。误码率是指错误接收的码元数在传输总码元数中所占的比例，更确切地说，误码率是码元在传输系统中被传错的概率，即误码率=错误码元数/传输总码元数。如果有误码就有误码率。误码的产生是由于在信号传输中，衰变改变了信号的电压,致使信号在传输中遭到破坏，产生误码。噪音、交流电或闪电造成的脉冲、传输设备故障及其他因素都会导致误码(比如传送的信号是1，而接收到的是0；反之亦然)。误码率是最常用的数据通信传输质量指标。它表示数字系统传输质量的式是“在多少位数据中出现一位差错”。

误信率，又称误比特率，是指错误接收的比特数在传输总比特数中所占的比例，即误比特率=错误比特数/传输总比特数。

在数字通信系统中，可靠性用误码率和误比特率表示。

数字调制用“星座图”来描述，星座图中定义了一种调制技术的两个基本参数：(1)信号分布；(2)与调制数字比特之间的映射关系。星座图中规定了星座点与传输比特间的对应关系，这种关系称为“映射”，一种调制技术的特性可由信号分布和映射完全定义，即可由星座图来完全定义。

二、QPSK系统的原理

四相相移调制是利用载波的四种不同相位差来表征输入的数字信息，是四进制移相键控。QPSK是在M=4时的调相技术，它规定了四种载波相位，分别为45°，135°，225°，275°，调制器输入的数据是二进制数字序列，为了能和四进制的载波相位配合起来，则需要把二进制数据变换为四进制数据，这就是说需要把二进制数字序列中每两个比特分成一组，共有四种组合，即00，01，10，11，其中每一组称为双比特码元。每一个双比特码元是由两位二进制信息比特组成，它们分别代表四进制四个符号中的一个符号。QPSK中每次调制可传输2个信息比特，这些信息比特是通过载波的四种相位来传递的。解调器根据星座图及接收到的载波信号的相位来判断发送端发送的信息比特。

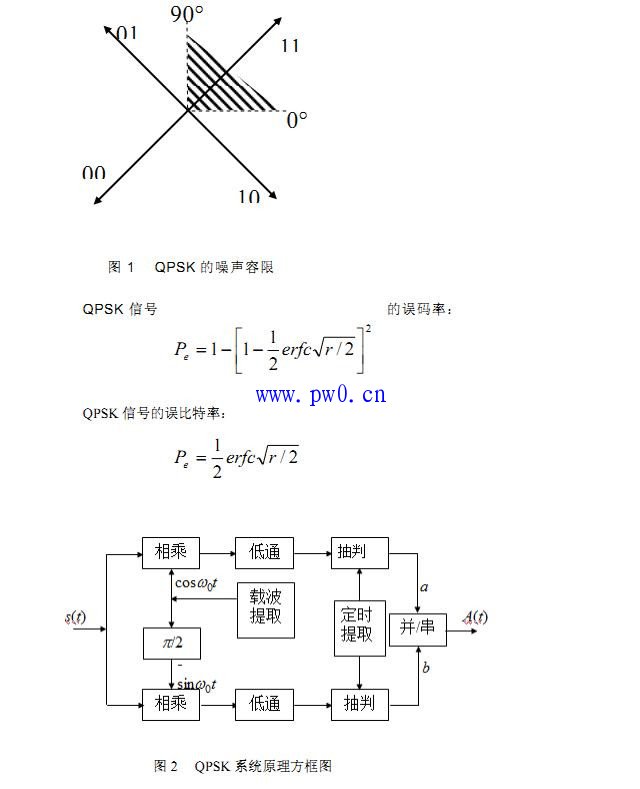
在QPSK体制中，由其矢量图(图1)可以看出，错误判决是由于信号矢量的相位因噪声而发生偏离造成的。例如，设发送矢量的相位为45°，它代表基带信号码元“11”，若因噪声的影响使接收矢量的相位变成135°，则将错判为“01”。当不同发送矢量以等概率出现时，合理的判决门限应该设定在和相邻矢量等距离的位置。在图中对于矢量“11”来说，判决门限应该设在0°和90°。当发送“11”时，接收信号矢量的相位若超出这一范围(图中阴影区)，则将发生错判。

对实验结果的简单分析和说明

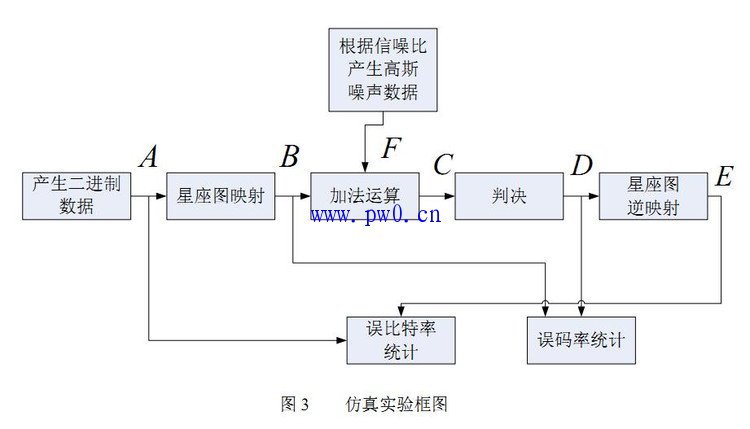
图4是B点信号的星座图映射，00、01、10、11组合分别映射成-1-j,-1+j,1-j,1+j。

图5是C点信号的星座图映射，它是加入噪声后的映射结果，由图中可以看出加入噪声后大致以-1-j,-1+j,1-j,1+j为中心形成了近似圆的图像，少部分点偏离比较严重，产生了误差。

由图6，可见QPSK仿真误码率曲线和理论误码率曲线重合在一起，QPSK仿真误比特率曲线和理论误比特率曲线也重合在一起，误码率约是误比特率的两倍，说明实验方法是正确可行的。

三、结论

本次实验研究了数字调制方式QPSK，对其误码率进行了考察。通过理论误码率和仿真误码的比较，了解了误码率的性能。本次实验还通过运用星座图来对实验结果进行仿真。本次实验得出结论如下：误码率是误比特率的两倍。

附录：

1、 心得体会：本次实验我收获很多，学会了应用MATLAB来处理问题，加深了对通信原理中部分公式和概念的理解。实验过程中也遇到了不少问题，在星座图映射上，一开始将00，01，10，11看成一个整体，这样对整体编程存在很大困难，因此后来尝试将其分开看，并成功映射；在计算噪声的过程中，由于通信原理的知识未能牢固掌握，在分析和计算的过程中花了很多时间；实验过程中，学会了使用find函数来代替for循环的功能，从而使程序运行更加快，大大加快了实验的进度。通过本次MATLAB的实践，应该加强MATLAB在各个学科的应用，学会用MATLAB来处理实际问题。

2、 程序：

Eb = Energy-per-bit

Es = Energy-per-symbol = nEb with n bits per symbol

Tb = Bit duration , Rb = Bit Rate, the bit transmission time Tb = 1/Rb

Ts = Symbol duration

N0 / 2 = Noise power spectral density (W/Hz)

Pb = Probability of bit-error

Ps = Probability of symbol-error

Eb/N0 = The energy per bit to noise power spectral density ratio。It is a normalized signal-to-noise ratio (SNR) measure, also known as the "SNR per bit".

SYMERR Compute number of symbol errors and symbol error rate.[NUMBER,RATIO] = SYMERR(X,Y) compares the elements in the two matrices X and Y. The number of the differences is output in NUMBER. The ratio of NUMBER to the number of elements is output in RATIO.

close all

clear all

SNR_DB=[0:1:12]; %Signal-to-noise ratio gradually improve

sum=1000000;

data= randsrc(sum,2,[0 1]); %generate a 1000000*2 random matrix, using [0 1]

[a1,b1]=find(data(:,1)==0&data(:,2)==0); %returns the row and column indices of the evaluated expression which are TRUE.

message(a1)=-1-j; % map [ 0 0] to 225°

[a2,b2]=find(data(:,1)==0&data(:,2)==1);

message(a2)=-1+j; % map [ 0 1] to 135°

[a3,b3]=find(data(:,1)==1&data(:,2)==0);

message(a3)=1-j; % map [ 1 0] to 275°

[a4,b4]=find(data(:,1)==1&data(:,2)==1);

message(a4)=1+j;% map [ 0 0] to 45°

scatterplot(message)

title('B点信号的星座图')

A=1;

Tb=1;

Eb=A*A*Tb;

P_signal=Eb/Tb;

NO=Eb./(10.^(SNR_DB/10)); %SNR_DB=10.*log10(Eb./NO)

P_noise=NO; %noise power 单边功率谱密度(N0)主要用在复数信号中，双边功率谱密度(N0/2)主要用在实信号中。

sigma=sqrt(P_noise);

for Eb_NO_id=1:length(sigma)

noise1=sigma(Eb_NO_id)*randn(1,sum);

noise2=sigma(Eb_NO_id)*randn(1,sum);

receive=message+noise1+noise2*j; %previously unconsidered: how to add gaussian noise to the original signal

resum=0;

total=0;

m1=find(angle(receive)0); %demodulate the [ 1 1] pattern

remessage(1,m1)=1+j;

redata(m1,1)=1;

redata(m1,2)=1;

m2= find( angle(receive)>pi/2&angle(receive)%demodulate the [ 0 1] pattern

remessage(1,m2)=-1+j;

redata(m2,1)=0;

redata(m2,2)=1;

m3=find( angle(receive)>-pi&angle(receive)%demodulate the [ 0 0] pattern

remessage(1,m3)=-1-j;

redata(m3,1)=0;

redata(m3,2)=0;

m4=find( angle(receive)>-pi/2&angle(receive)%demodulate the [ 1 0] pattern

remessage(1,m4)=1-j;

redata(m4,1)=1;

redata(m4,2)=0;

[resum,ratio1]=symerr(data,redata); % 'symerr' Compute number of symbol errors and symbol error rate

pbit(Eb_NO_id)=resum/(sum*2); %1000000 symbols -->2000000 bits QPSK: 2bits per symbol

[total,ratio2]=symerr(message,remessage); %Compute number of symbol errors and symbol error rate

pe(Eb_NO_id)=total/sum; % Calculated according to the definition

end

scatterplot(receive)

title('C点信号的星座图')

Pe=1-(1-1/2*erfc(sqrt(10.^(SNR_DB/10)/2))).^2;

Pbit=1/2*erfc(sqrt(10.^(SNR_DB/10)/2));

figure(3)

semilogy(SNR_DB,pe,':s',SNR_DB,Pe,'-*',SNR_DB,pbit,'-o',SNR_DB,Pbit,':+')

legend('QPSK仿真误码率','QPSK理论误码率','QPSK仿真误比特率','QPSK理论误比特率',1)

xlabel('信噪比/dB')

ylabel('概率P')

grid on