【通信原理 入坑之路】——理解符号同步方法之：早迟门法（Early-late Gate）

我们知道在数字通信系统中，除了载波同步，帧同步外，符号同步也是至关重要的一环。因为数字通信系统中的消息都是一个一个按着节拍发的，所以我们在接收这些符号的时候，也需要按照一个时钟打着节拍一个一个接收。但是如果这个时钟出现了偏差，就会导致我们接收的位置发生偏移导致误码。因此本文将介绍一种经典的闭环符号同步方法——早迟门法。

我们首先来看看早迟门电路的组成：

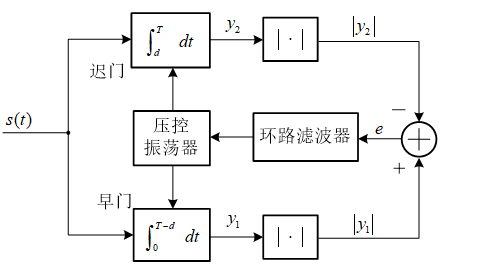
其中，早门和迟门分别是两个在一个码元周期 T 内，积分区间分别取 $(0,T-d),(d,T)$ 的积分器。早迟门法基于下面的一个原理：

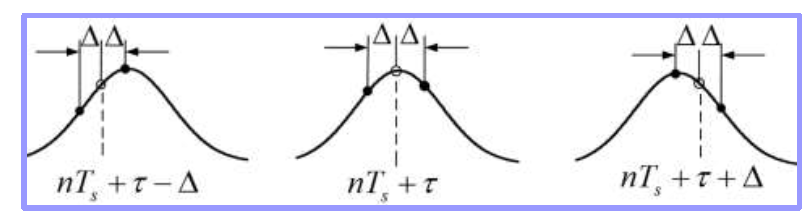
其中曲线波形就表示一个码元的波形，我们认为一个码元的波形是对称的，其中的虚线就表示我们的采样点。很明显，如果采样点在波形的峰值，那么就是正确的采用，但是采样点可能会因为时钟的偏差而发生偏移，就会导致采用到了其他的地方，那么如何矫正呢？

我们下面看看早门和迟门具体是怎么操作的：首先看一个时钟正确的情况：

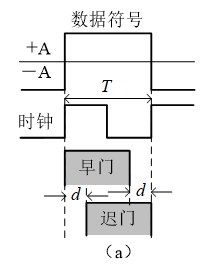
此时很明显时钟是正确的，早门就是在区间 $(0,T-d)$ 上对接收到的数据波形进行积分：$$y_1={\int }_0^{T-d}Adt=(T-d)A$$
然后看上面的电路图，我们是需要对积分结果取绝对值的，这里还是：$(T-d)A$。

下面我们看看迟门：在区间 $(d,T)$上对数据波形进行积分：$$y_2={\int }_d^{T}Adt=(T-d)A$$
我们发现，取完绝对值之后，两者相减，结果为0。早门和迟门在各自区间上积分的绝对值一样，因此这就意味着我们现在的时钟是正确的，暂时保持这样的节拍进行采样就对了！

下面我们再来看看如果时钟发生了偏移会是什么情况：

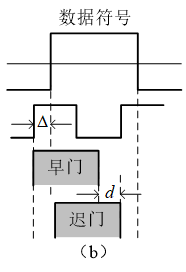
早门在对应区间的积分结果是：$$y_1={\int }_0^{△}(-A)dt+{\int }_{△}^{T-d}Adt=(T-d-2△)A$$
迟门在对应区间的积分结果是：$$y_2={\int }_0^{T-d}Adt=(T-d)A$$

两者绝对值的差为：$$e=|y_1|-|y_2|=-2△A<0$$

说明迟门的积分值比较大，也就是下面这个情况：

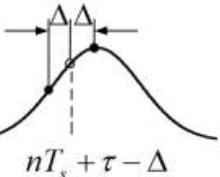
所以意味着我们的采样点需要右移，差值 $e$ 经过环路滤波器之后将会告诉压控振荡器应该如何调节。这样就实现了采样偏移的矫正。

不过需要指出的是：早迟门法不适合那种拥有很长一串0或1序列的符号同步，因为如果有很长一串相同的符号，那么不管时钟是否偏移早迟门积分的结果都会是一样的，这样就无法做到时钟的矫正，因此如果需要使用早迟门，那么在进行系统设计需要保证符号序列不会有很长的连0或连1.

最后

以上就是迅速冥王星为你收集整理的【通信原理 入坑之路】——理解符号同步方法之：早迟门法（Early-late Gate）的全部内容，希望文章能够帮你解决【通信原理 入坑之路】——理解符号同步方法之：早迟门法（Early-late Gate）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。