MATLAB之Simulink(四)两位二进制数加法器

##MATLAB之Simulink(四)
##两位二进制数加法器

在上一节中，我们学习了全加器的原理并且进行了仿真，今天我们来做一个实例——两位二进制数的加法器。

由于全加器有三个输入，其中一个是由低位的进位输入进来的，但是最低位只有两个输入，所以两个最低位相加不能用加法器，那么应该如何相加呢？这里给大家介绍另一种加法器——半加器。

半加器定义：
两个1位二进制数相加，若只考虑了两个加数本身，而没有考虑由低位来的进位的运算称为半加，而实现半加运算的逻辑电路称为半加器。

也就是说，半加器仅适用于一位二进制数的相加，不需要考虑低位的进位。所以我们需要用到一个半加器和一个全加器，半加器用来计算两个低位的结果，全加器用来计算两个高位的结果，同时考虑低位的进位。
一般情况下，用A、B来表示两个一位二进制加数，用S表示A、B的和，C表示A、B的进位。

先来仿真一下半加器：
列出真值表

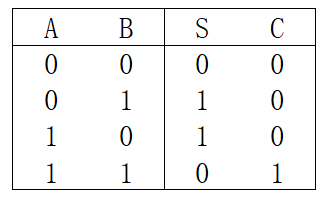
得出表达式：


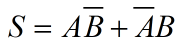
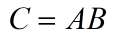
根据表达式，很容易可以作出半加器的模型
（过程这里不再多说，不懂得朋友请看我的上一篇全加器的文章）
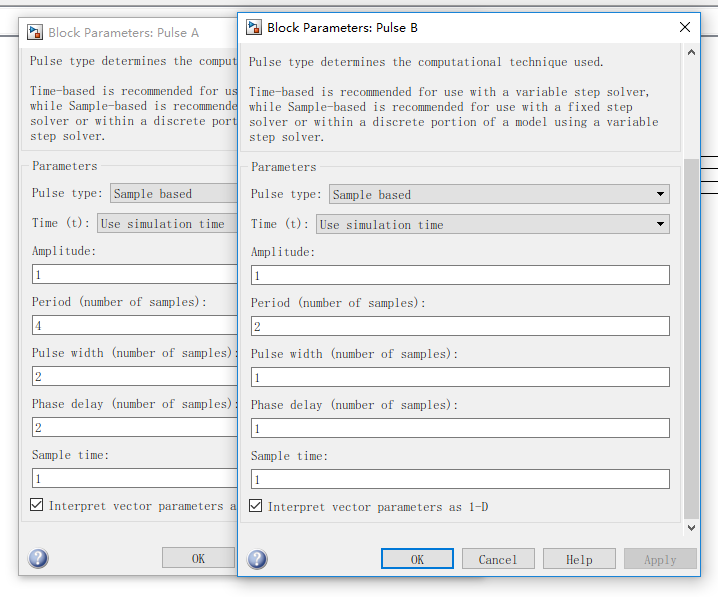
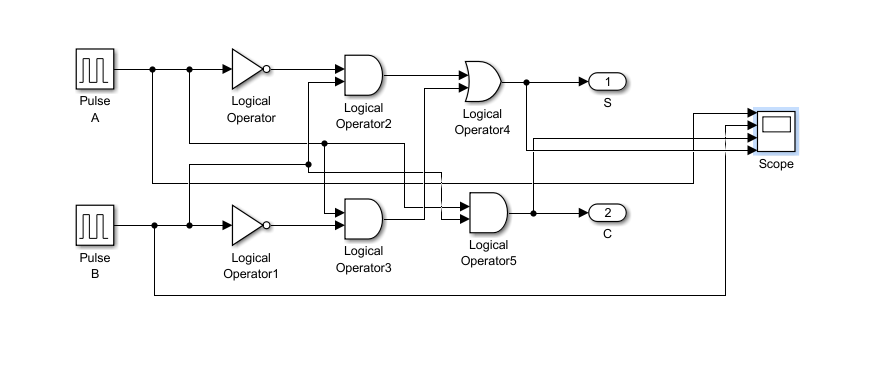我们假设输入的数分别为00、01、10、11，那么输入矩形波的设置应该是这样：
我们用示波器连接两个输入和两个输入，观察仿真结果：

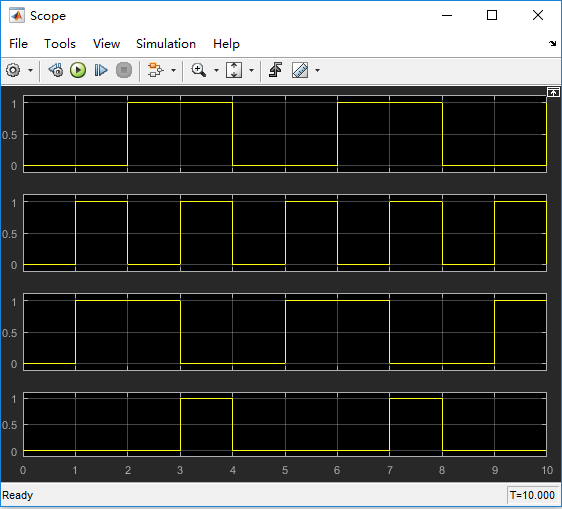
这里有四行波形，第一行为加数A，第二行为加数B，第三行为S，第四行为C。
不难看出，仿真结果与真值表相对应，半加器仿真成功！

接下来，我们直接将一个半加器和一个全加器合并在一起稍微修改，就可以得到一个两位二进制数的加法器：

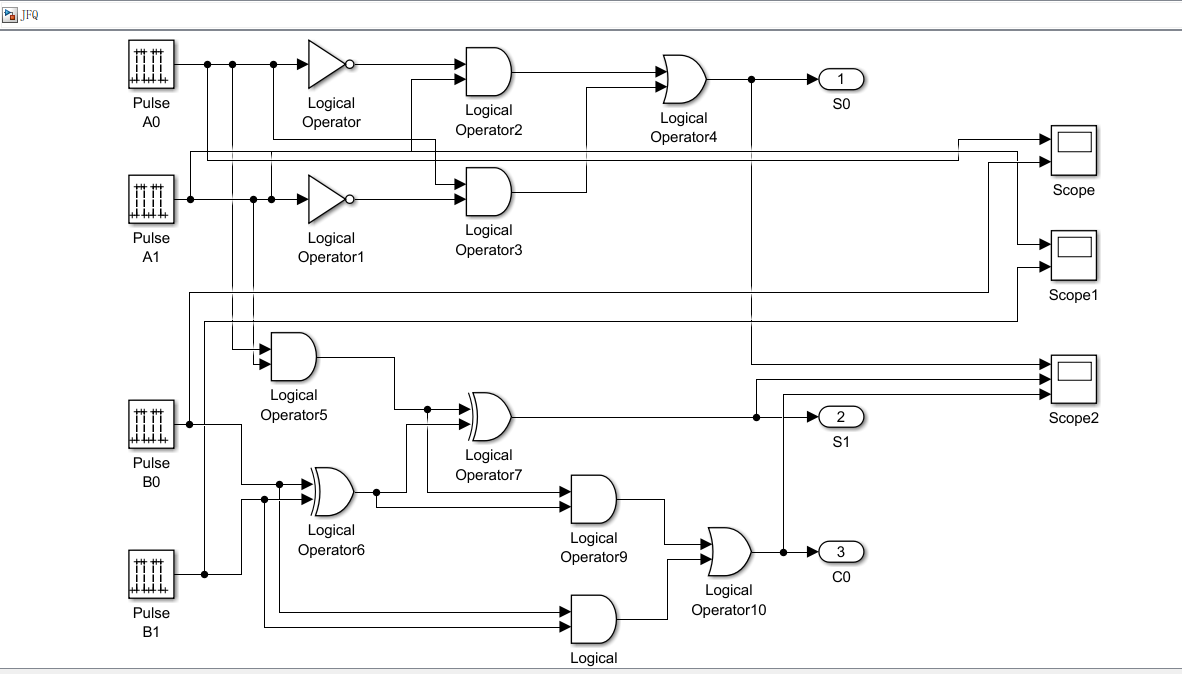这里需要注意的是，半加器用来计算两个低位，全加器用来计算两个高位，全加器中的进位输入由半加器的进位输出连接。
在这幅图中，A0，A1表示两个低位，B0，B1表示两个高位。
我们用三个示波器分别表示第一个加数、第二个加数和结果。

接下来我们看仿真结果：
第一个加数：

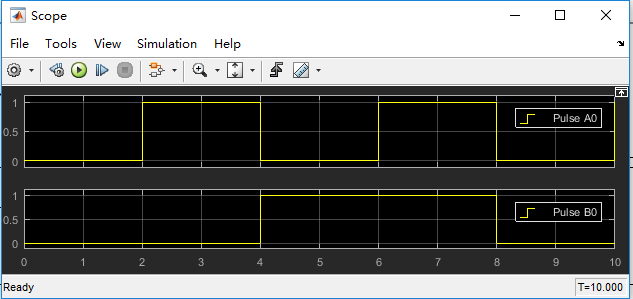
第二个加数：
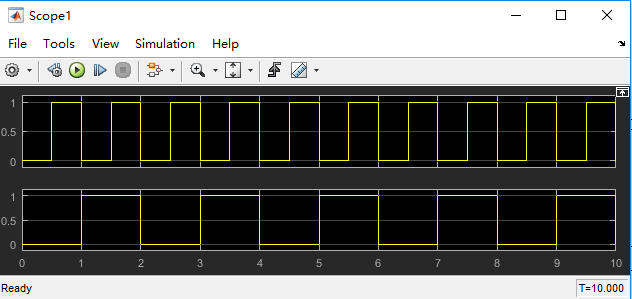结果：

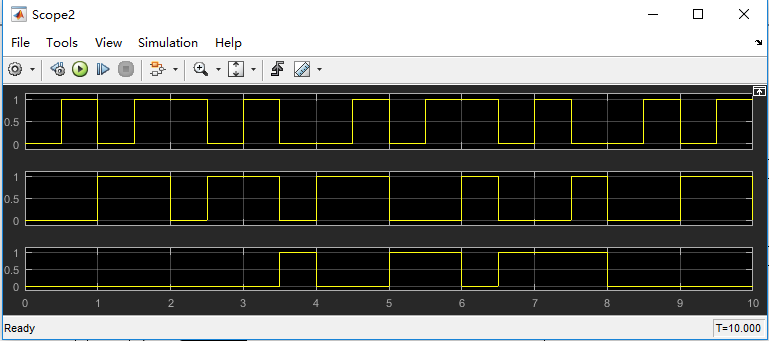
注意：每幅图都是低位在上，高位在下。

我们进行验证，不难发现仿真结果正确。

这就是两位二进制加法器的仿真过程，掌握这个方法后很容易设计出多位二进制加法器，没错，只要增加几个全加器就可以了。

##以上就是本节的全部内容，后续内容会逐渐上传，相关源码也会统一上传，也可以到公众号私聊我要。

##不足之处请及时指出，相互学习
##不懂得小伙伴可以到我的公众号"歌者X"私信我，看到后会回复的，欢迎交流学习！
下面是我的公众号

最后

以上就是虚心人生为你收集整理的MATLAB之Simulink(四)两位二进制数加法器的全部内容，希望文章能够帮你解决MATLAB之Simulink(四)两位二进制数加法器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。