link
在数字电路系统中,乘法器是一种不可或缺的运算单元。数字信号处理、卷积运算的本质上是对乘法操作的复用,因此在运用数字电路系统进行信号处理时,往往要用到各种各样的乘法器。不同乘法器的性能、功耗依赖于设计的电路结构。近年来,对于优化乘法器结构设计,提高运算效率的研究层出不穷,乘法器的发展也日趋成熟。本文将介绍几种典型的乘法器结构,包括阵列乘法器、改进的booth编码乘法器,以及介绍Wallace tree压缩结构对部分积求和速度的影响。
1.乘法运算过程
在数字系统中,乘法运算是以二进制的形式进行的,假设乘数为A,被乘数为B,那么写成二进制数为
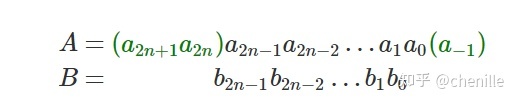
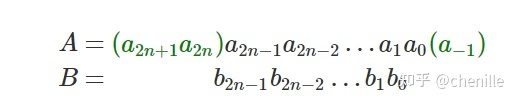
其中 a−1a_{2k-1}+a_{2k}-a_{ak+1} )的值,也就是乘数A相邻三位的值。因此依据乘数A的相邻三位进行编码,可以得出部分积对应的操作。这种编码方式被称为基4-booth编码。
由公式可知:采用基4-booth编码乘法器的部分积只有位数的一半。
由推导的公式可以得出基4-booth乘法器的编码表
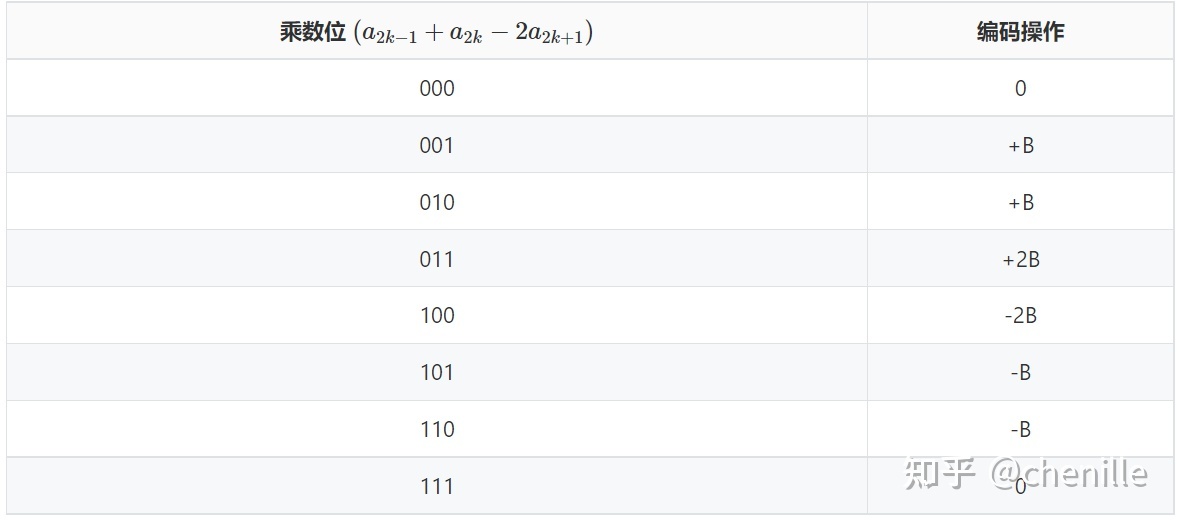
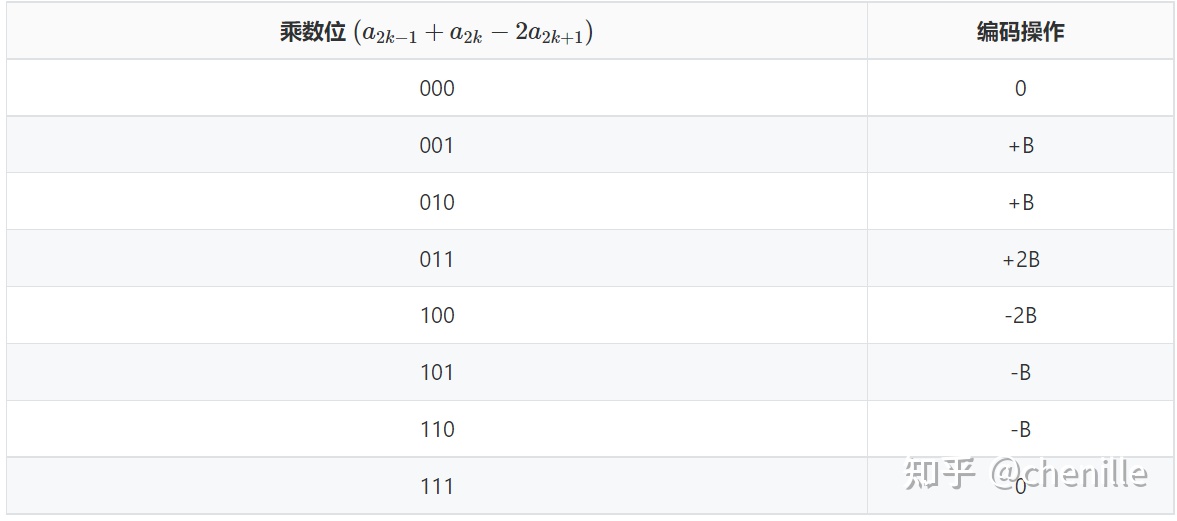
具体操作过程如下:
假设A=1001,B=1101


在乘数A的末尾补上0,前面补上符号位,然后对乘数A的每三位进行booth编码,编码数{0,-1,1,-2,2}分别对应无操作、-B、+B、-2B、+2B五种部分积的操作。每次进行部分积求和操作前左移2位。因此:
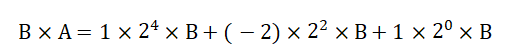
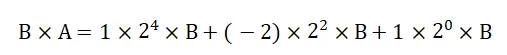
运算过程:


与传统的乘法计算过程相比,采用booth编码的方式能够使运算产生的部分积减少一半,从而大大减少后续的求和操作次数,节省了运算资源,降低延时,性能得到提升。
4.Wallace tree压缩
经过booth编码并输出相应的部分积后,下一步要进行的是对部分积进行求和,这个过程可以使用阵列加法器来完成,但部份积较多的情况下,用加法器阵列来求和效率不高,并且消耗的加法器运算资源较多,乘法器运算时间取决于最长路径延时。为了提高乘法器的运算速度,节省运算资源,C.S.Wallace提出了树形部份积压缩的方法,后人称之为Wallace 树压缩。其方法思想是:采用进位保留加法器(CSA),将三行部份积压缩成sum和carry两行,然后再输入下一级CSA中,进行进一步的压缩,直到最后剩下两行,采用进位传播加法器(Carry propagating adder)相加得到最后的乘法结果。
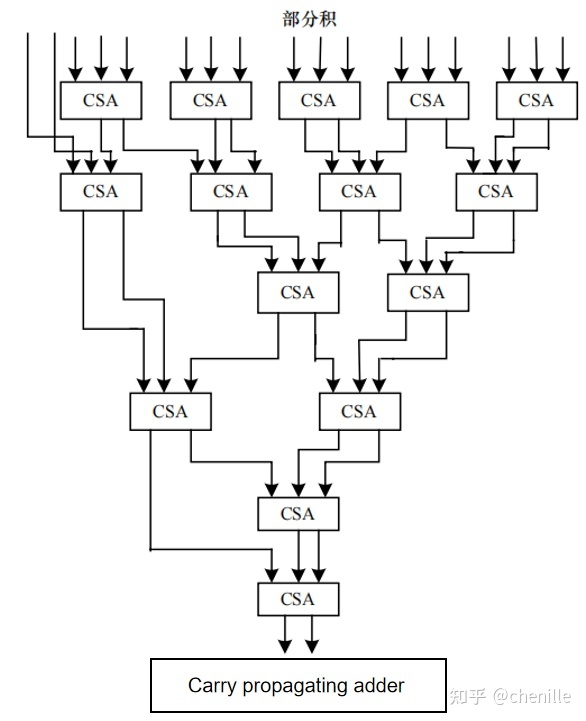
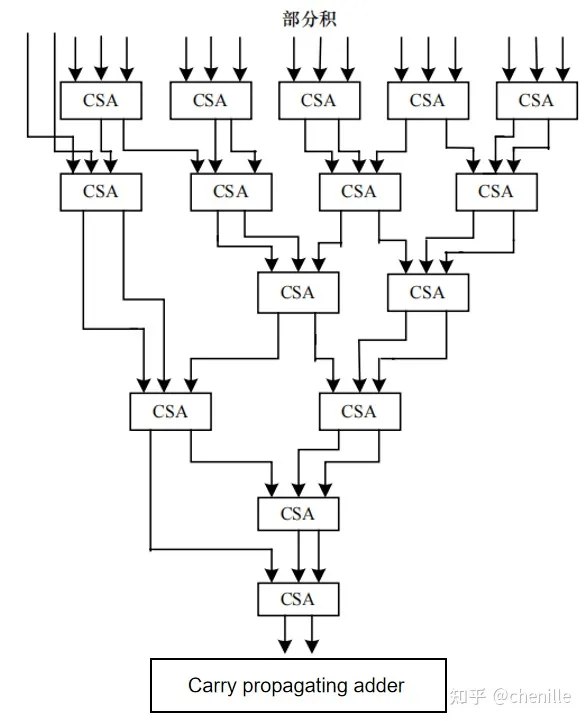
具体3-2压缩过程:
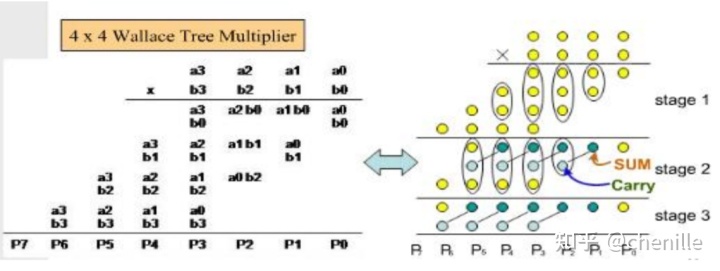
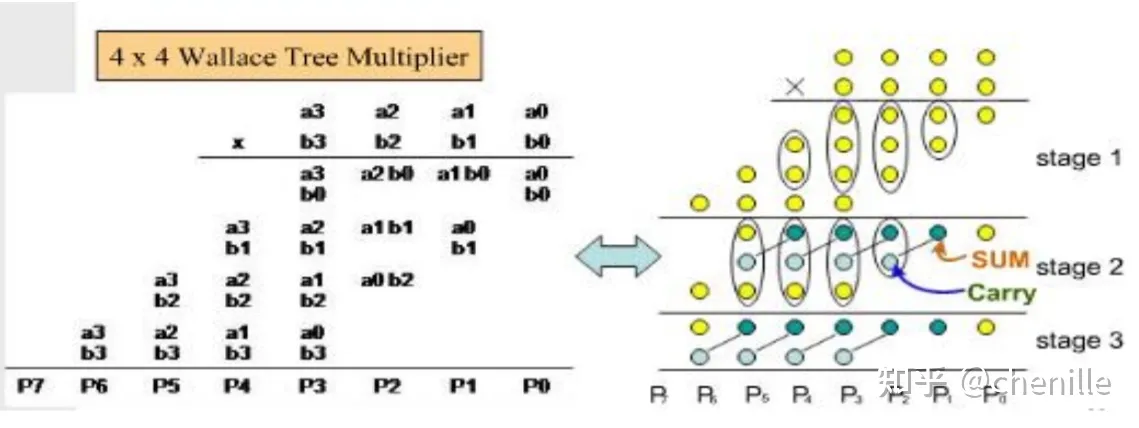
最后
以上就是幽默咖啡豆最近收集整理的关于数字电路设计(4)——乘法器 chenille chenille的全部内容,更多相关数字电路设计(4)——乘法器内容请搜索靠谱客的其他文章。








发表评论 取消回复