用MATLAB玩转机器人--第六章 用MATLAB玩转单关节机器人

1. 概述

使用 simulink 搭建《用MATLAB玩转机器人》的第六章——单关节机器人的仿真，详细记录并积累 simulink 的使用技巧。

2. 仿真搭建

对于单关节机器人的位置控制，大致分为四个过程：

1. 规划出单杆自由端的运动轨迹函数，分为加速、匀速、减速三个区间
2. 建立机器人的机械、电气模块的数学模型
3. 设计控制系统的数学模型
4. 根据上述过程建立的数学模型进行仿真搭建并仿真。

另外，单关节机器人位置控制的仿真总共分为四个模块另：
     a. 运动轨迹函数生成模块
     b. PID控制器及输出限幅模块
     c. 减速器与传动装置模型
     d. 单杆的运动模型

2.1 运动轨迹函数

运动轨迹函数分为三个部分
(1)加速区间 0≤t≤2Δ
$${\eta }_{加速}(t)=\frac{\pi }{4{\Delta }^2}{t}^3-\frac{\pi }{16{\Delta }^3}{t}^4\text{\hspace{1em}(6-1)}$$
(2)匀速区间 2Δ≤t≤2.5-2Δ
$${\eta }_{匀速}(t)=(t-\Delta )\times \pi \text{\hspace{1em}(6-2)}$$
(3)减速区间 2.5-2Δ≤t≤2.5
$${\eta }_{减速}(t)=2\pi -\Delta \pi +\pi (t-2)-\frac{\pi }{4{\Delta }^2}(t-2{)}^3+\frac{\pi }{16{\Delta }^3}(t-2{)}^4$$

1. Source 中拖入clock ，Commonly used blocks中拖入subsystem，将两者连线后，把Subsystem改为trajectory。
   
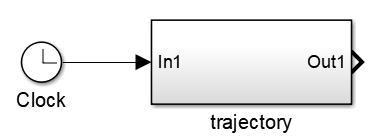
2. 双击Subsystem，将In1改为t，Out1改为theta*(t)
   
   
   观察在主系统中的改变
   
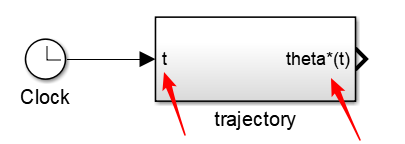
3. 绘制 0≤t≤2Δ 的时间区间
   
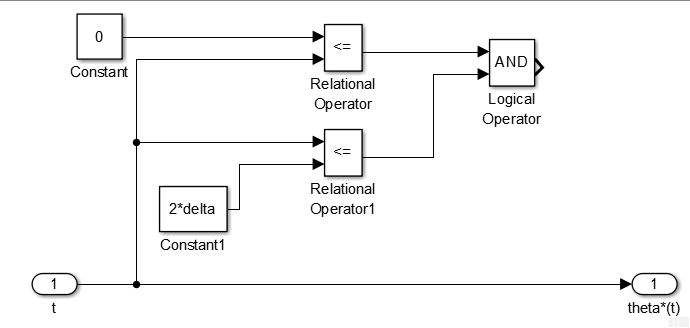
4. 拖入Enabled Subsystem，并连线
   
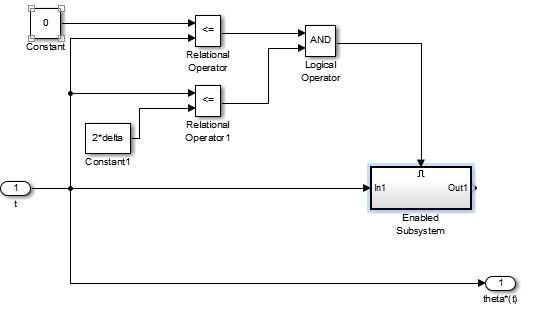
5. 双击Enabled Subsystem，进入子系统输入公式（6-1）
   (1)加速区间 0≤t≤2Δ加速区间 0≤t≤2Δ
   $${\eta }_{加速}(t)=\frac{\pi }{4{\Delta }^2}{t}^3-\frac{\pi }{16{\Delta }^3}{t}^4\text{\hspace{1em}(6-1)}$$

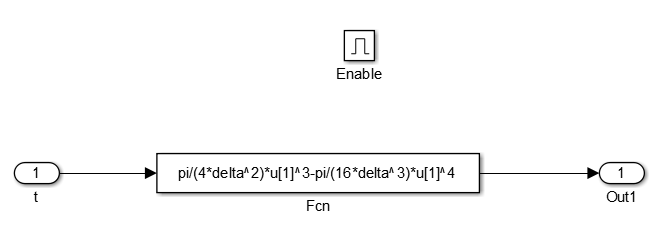
公式（6-1）中的 t 即为子系统的输入 t，也为图中 u[1].
6. 采用同样的方法，分别绘制匀速区间、减速区间，公式如下：
(2)匀速区间 2Δ≤t≤2.5-2Δ
$${\eta }_{匀速}(t)=(t-\Delta )\times \pi \text{\hspace{1em}(6-2)}$$
(3)减速区间 2.5-2Δ≤t≤2.5
$${\eta }_{减速}(t)=2\pi -\Delta \pi +\pi (t-2)-\frac{\pi }{4{\Delta }^2}(t-2{)}^3+\frac{\pi }{16{\Delta }^3}(t-2{)}^4$$

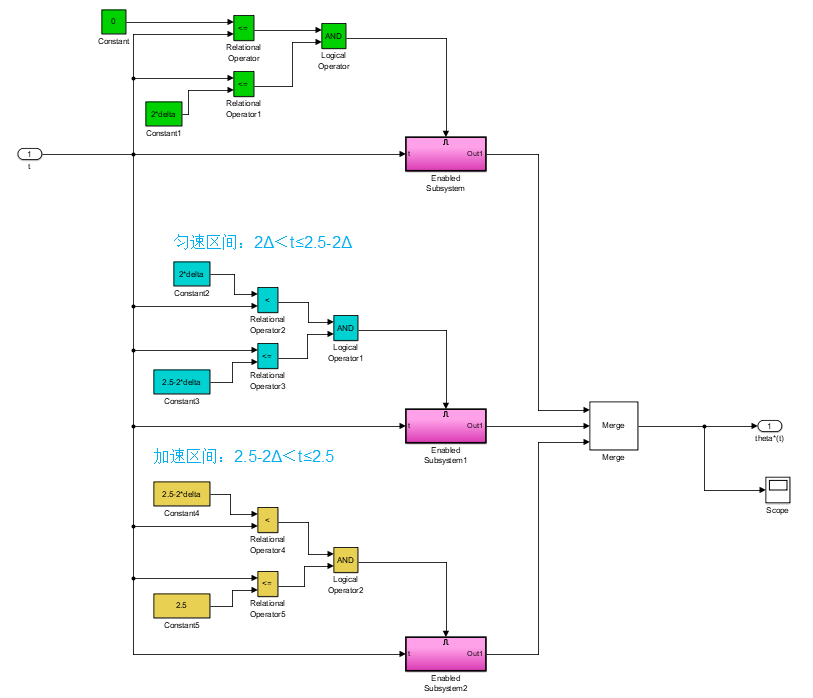
图中，示波器是为了观察轨迹函数的输出，merge 模块则参考链接simulink模块使用记录2-EnabledSubsystem/merge

2.2 机器人的机械仿真模型

单杆的数学模型为：
$$\tau =(m_1{r}_1^2+I_{zzg1})\times {\ddot{\theta }}_1+c_1{\dot{\theta }}_1\text{\hspace{1em}(6-4)}$$
单杆运动时，输入时扭矩 τ、输出是转角 ${\theta }_1$、$m_1$、$r_1$、$I_{zzg1}$、$c_1$是常量。
将公式（6-4）变形如下，按照下面的公式建立仿真模型：
$${\ddot{\theta }}_1=\frac{1}{m_1{r}_1^2+I_{zzg1}}(\tau -c_1{\dot{\theta }}_1)\text{\hspace{1em}(6-5)}$$

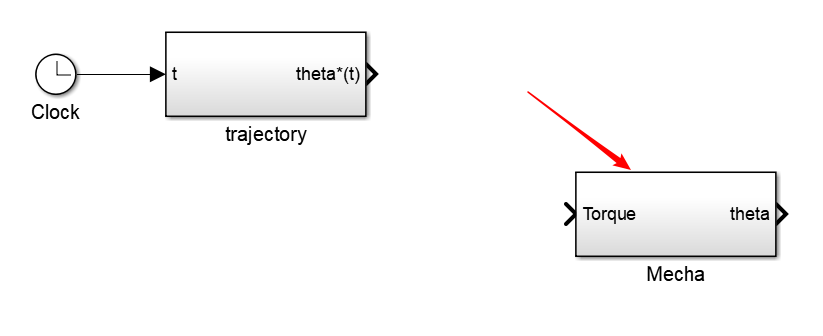
1. 拖入subsystem，双击后，将上述公式建立仿真
   
   
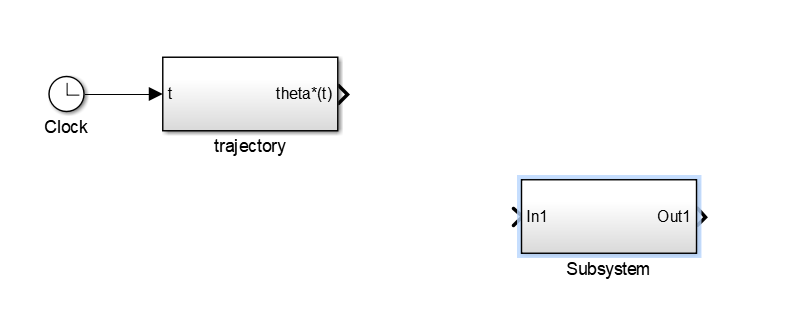
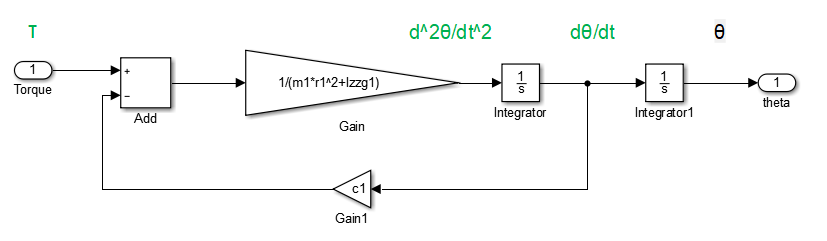
   子系统内部模块建立后，将子系统命名为Mecha，如下图
   

2.3 机器人的电气仿真模型

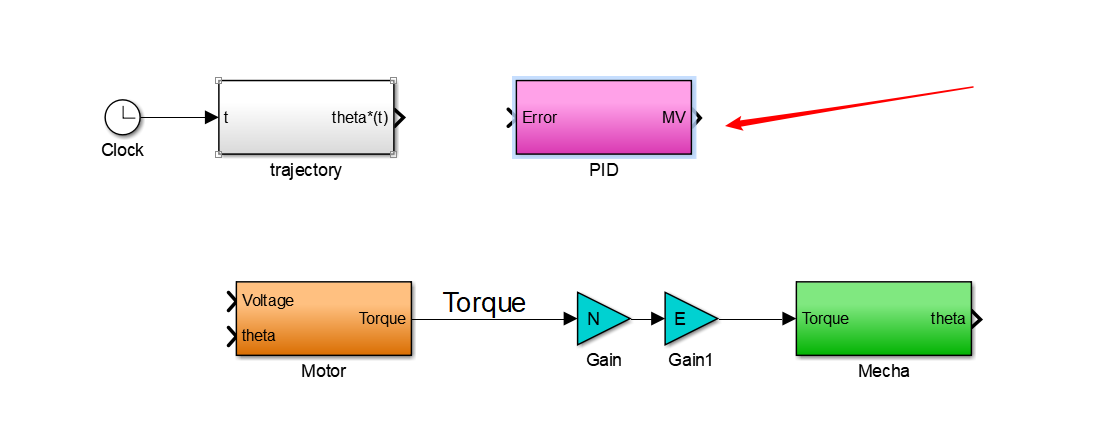
在simulink中新建ch6_sim模型文件，搭建如下系统。

2.3.1 直流电机部分

直流电机的电气结构数学模型为：
$$T_e=K_t{i}_a\text{\hspace{1em}(6-6)}$$
$$T_e=T+(J\ddot{\theta }+B_m\dot{\theta })\text{\hspace{1em}(6-7)}$$
$$i_a(s)=\frac{1}{L_{a}s+R_a}v(s)-\frac{K_{e}s}{L_{a}s+R_a}\theta (s)\text{\hspace{1em}(6-8)}$$
式中，$T_e$是电机产生的转矩（N·m）；$K_t$是转矩常数（N·m/A）；J是转子的惯性力矩（kg·$m^2$）;$B_m$是旋转运动的粘性摩擦系数；T是将要传递到负载侧（单杆）的力矩（N·m）；θ表示旋转角度；$\dot{\theta }$表示旋转角速度（rad/s）；$\ddot{\theta }$表示角加速度(rad/$s^2$);v为输入电压(V)；$i_a$为转子电流（A）；$R_a$为转子电阻（Ω）；$L_a$是转子电感（H）；$K_e$是逆启动转矩系数[V/(rad/s)]。

1. 拖入subsystem,双击进入
   
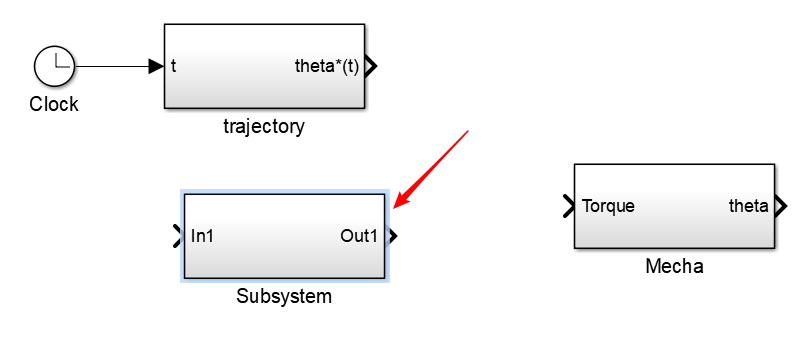
2. 从Ports&& Subsystems中拖入In1
   
3. 将直流电机电气部分的仿真模型构建出来，即公式（6-6）、（6-7）、（6-8）
   
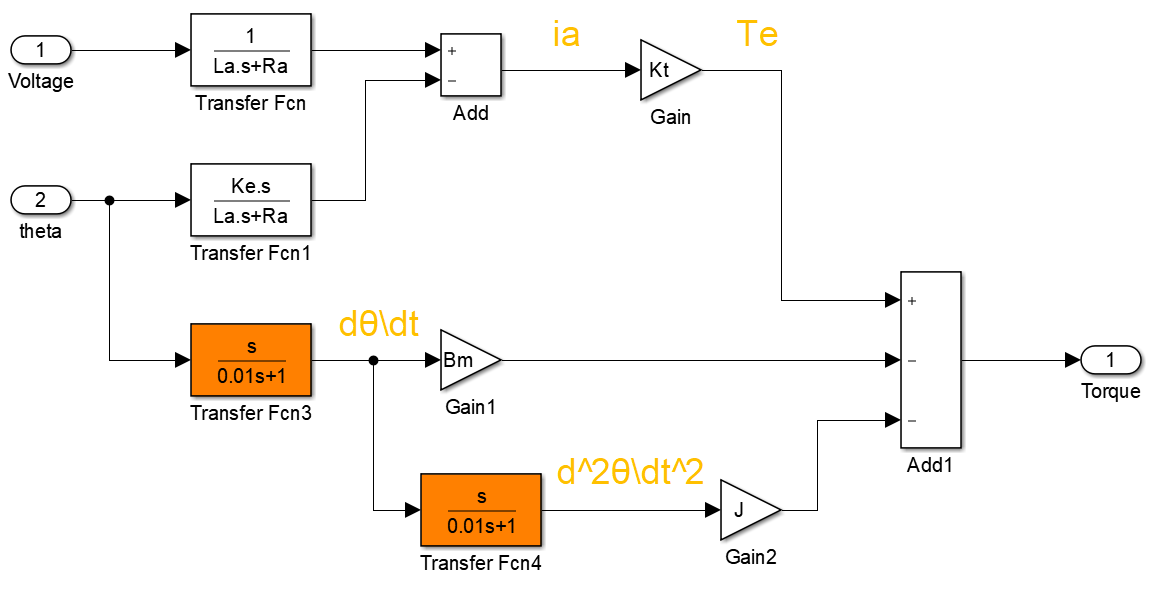
   图中，输入Voltage和theta分别是公式（6-8）中的 v(s) 和 θ(s)。输出Torque是将要传到负载侧（单杆）的力矩 T，由公式（6-7）变形得到$$T=T_e-(J\ddot{\theta }+B_m\dot{\theta })\text{\hspace{1em}(6-9)}$$
   另外，图中的橘黄色部分原本是春微分环节 s ，但在一般情况下，淡村的微分环节容易受到高频噪声的干扰（实际上，表现为纯粹的微分特性的器件在现实生活中是很难纯在的），故采用了近似微分$\frac{s}{0.01s+1}$。
   近似微分是给纯微分环节串联一个影响较小的低通滤波器$\frac{1}{as+1}$变成$\frac{s}{as+1}$的形式，这里a=0.01。

2.3.2 减速器与传动装置

由公式（6-9）得到的 T 是由电机将要传递到负载侧（单杆）的力矩。考虑到齿轮传动中滑动摩擦等因素，在直流电机侧的输出扭矩 T 传递到负载侧时还会损失一部分的能量。
摩擦损失与电机侧输出扭矩 T 成比例，摩擦损失比例系数为 c ，则传到单杆的转轴一侧的单杆扭矩 ${\tau }_2$ 为
$${\tau }_2=N(T-cT)=N\times (1-c)\times T=N\times E\times T$$
为了描述方便，将电机侧输出力矩 T 改名为 ${\tau }_1$，即${\tau }_1$=T，则上式为：$${\tau }_2=N\times E\times {\tau }_1\text{\hspace{1em}(6-10)}$$，式中，E = 1-c 被称为传导系数。
用公式（6-9）得到的结果再乘以系数 N 和 E 后，就是最终驱动单杆转动的力矩 ${\tau }_2$。
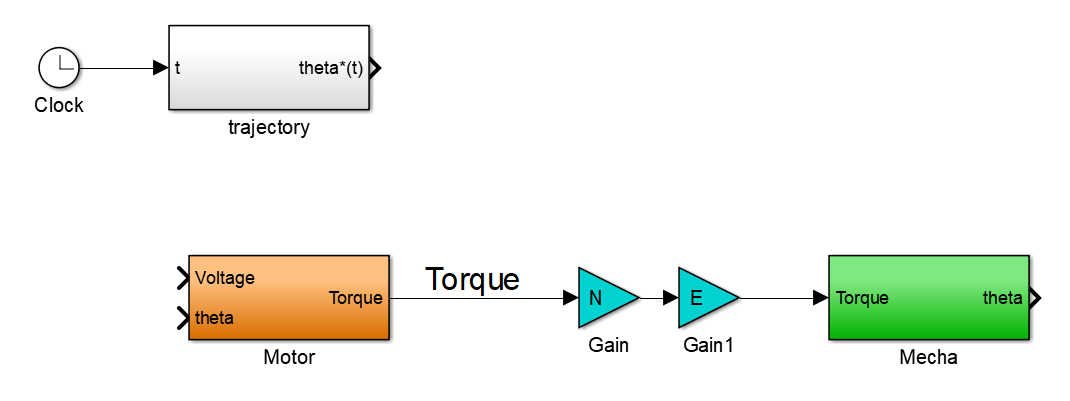
在simulink中完成减速器与传动装置的仿真模型。

2.4 PID 控制的仿真模型

PID 控制器的仿真由两部分构成，一部分是 PID 控制子模块，一部分是输出限幅模块Saturation。

2.4.1 PID 控制器的仿真模型

PID 控制器的传递函数为：
$$D(s)=\frac{U(s)}{E(s)}=K_p[1+\frac{1}{s{T}_I}+s{T}_D]\text{\hspace{1em}(6-11)}$$，用近似微分代替微分：$$D(s)=K_p[1+\frac{1}{s{T}_I}+\frac{s{T}_D}{as{T}_D+1}]\text{\hspace{1em}(6-11)}$$

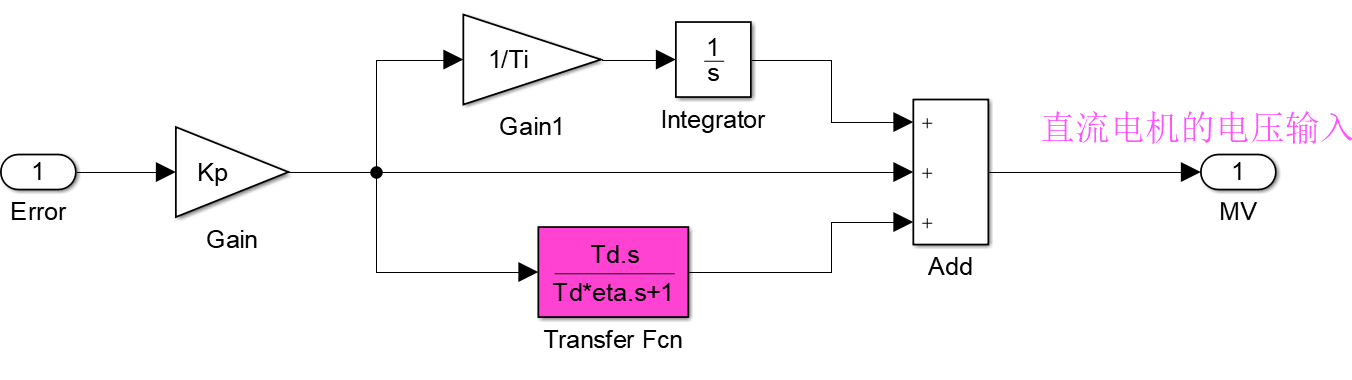
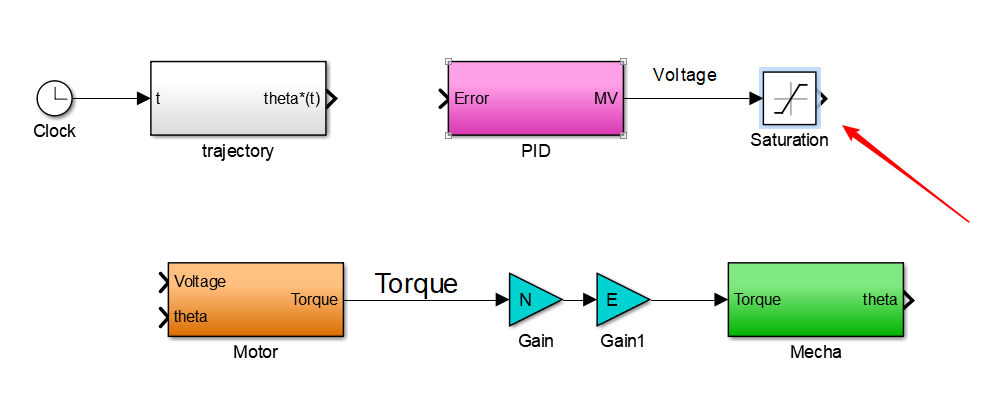
2.4.2 PID 输出量的上下限设定

PID控制器的输出量是直流电机的输入电压，因为直流电机的输入电压是有上下限的，如果超出限制则有可能造成电机的损坏。
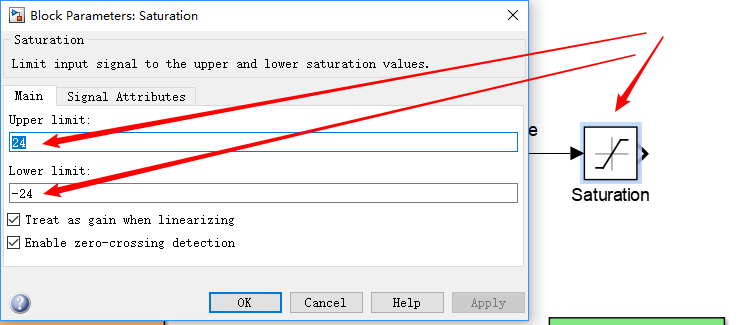
上下限的设置通过Saturation Block(饱和模块)实现，将上下限分别设定为 +24 和 -24，即设定 PID 控制器输出的值将被限定在电压±24V 范围内再传递给直流电机。

2.5 构建整体仿真模型

1. 因为 PID的输出是直流电机的电压，故Saturation后接Moter的Voltage
   
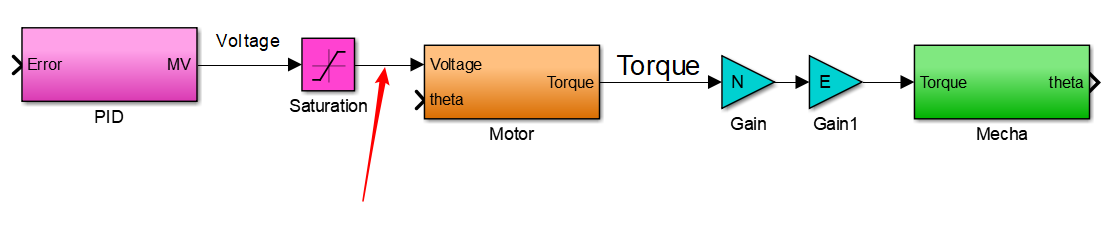
2. 又系统的输出是角度θ，故偏差应该是期望角度与输出角度的差值，以此作为 PID 控制器的输入，故连线如下：
   
3. 在直流电机的仿真模块，由于公式（6-8）中用到θ(s)，故需要将输出引到Motor的输入中去。
   
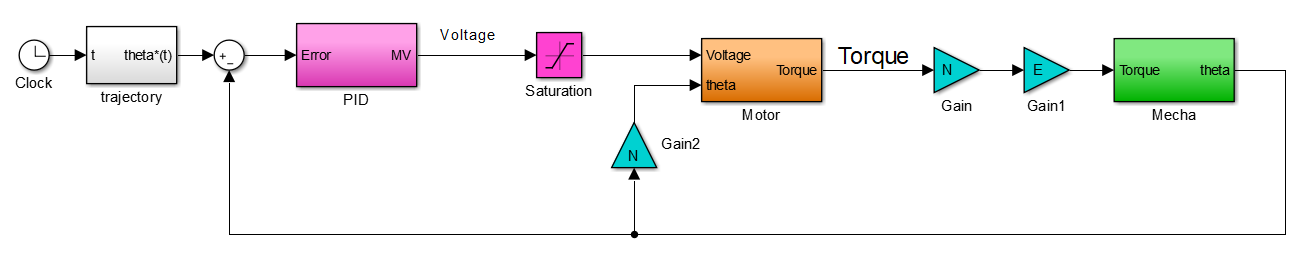
   这里需要解释下增益N，即
         $thet{a}_{Mecha}\times N=thet{a}_{Motor}$
   这是由于在直流电机模块中，存在的减速器。假设减速器链接的齿轮1和齿轮2的齿数分别为 $n_1$ 和$n_2$，则变速比 N 为：
            $N=\frac{n_2}{n_1}$
   当直流电机的旋转角度为 ${\theta }_1$,单杆的旋转角度为 ${\theta }_2$ 时，
           ${\theta }_1=N\times {\theta }_2$
   角度的变比正好与扭矩的变比相反。
4. 拖入goto和from，并将from接到示波器，便于观察图形

• 在trajectory的输出接goto，信号为设定的角度 θ
• 在saturation的输出接goto，信号为 PID 输出的直流电机控制电压
• 在Mecha输入处接goto，信号为电机输出到单杆侧的扭矩
• 在Mecha的输出接goto，信号为系统输出的角度 θ
• 将四路goto信号对应的from接到示波器，如图。
  
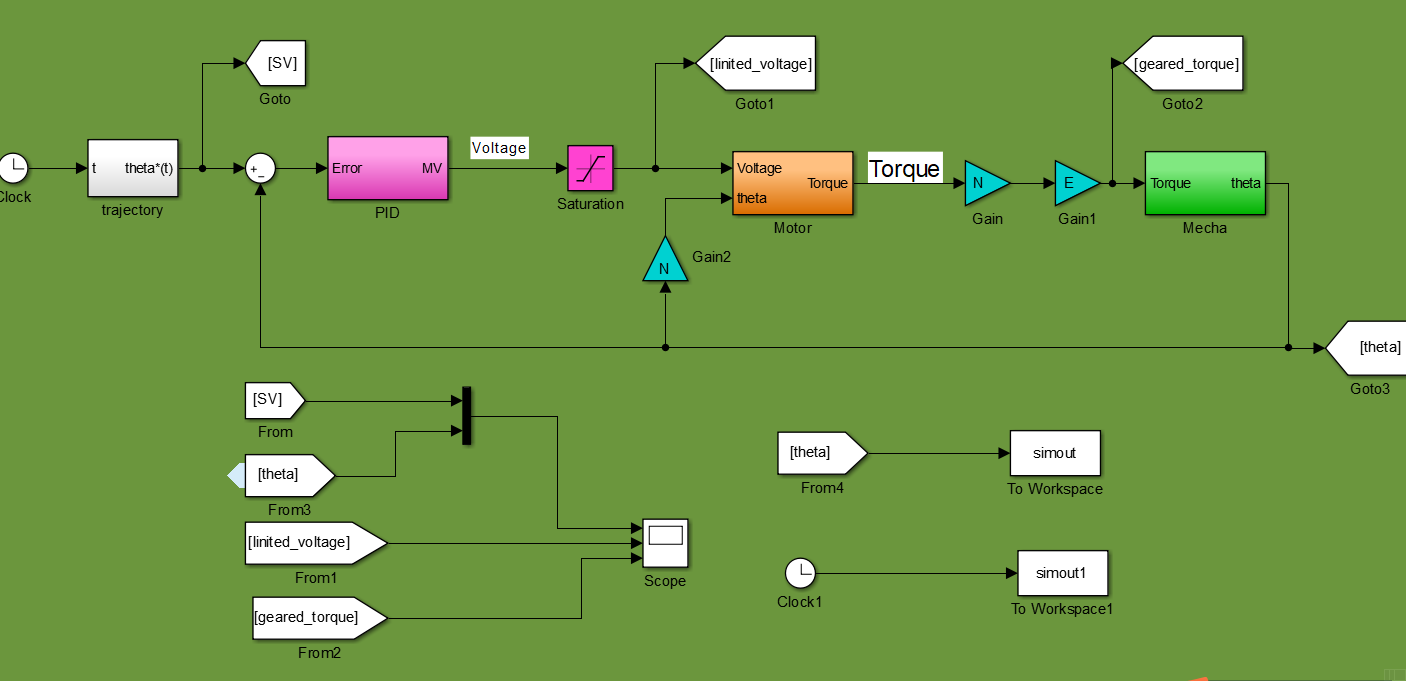
  至此，单关节机器人的仿真搭建基本完成了。

3. 函数编写

3.1 initial_patam.m函数的编写

新建initial_patam.m函数，在此输入仿真所需要的初始化参数

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% initialize_para.m
% 第6章 参数设置
% 轨迹函数，机械和电气系统，减速器和控制器的PID参数
%
% Version 1.0 by Hiroumi Mita, CYBERNET SYSTEMS CO.,LTD.
% Version 1.5 by Hongtao Zhang, 2016/08/12 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clc;              % 清屏
close all;        % 关闭所有
clear;        % 清除所有变量

% 轨迹函数的参数
delta = 0.25;     % 轨迹函数中的 delta变量

% 机械参数
l1 = 0.2;         %杆长 单位：[m]
w1 = 0.01;        %杆宽[m]
h1 = 0.004;       %杆高[m]
r1 = 0.1;         %从杆端点到重心位置的长度[m]，r1=0.5*l1
ro = 2690;         %杆的材料密度 单位：[Kg*m^3]
m1 = l1*w1*h1*ro;  %杆的质量[Kg]
Izzg1 = (1/12)*m1*(w1^2+l1^2); %杆的转动惯量，zz[kg*m^2]
Ixxg1 = (1/12)*m1*(w1^2+h1^2); %杆的转动惯量，xx[kg*m^2]
Iyyg1 = (1/12)*m1*(l1^2+h1^2); %杆的转动惯量，yy[kg*m^2]
c1 = 0.001;       %杆的粘性系数[N*s/rad]

% 电气参数
Ra = 10;     %电机电阻值[OM]
La = 4.4e-3; %电机电感值[H]
Kt = 0.05;   %扭矩常数[N*m/A]
Ke = Kt;     %反电力常数[V*s/rad]
J = 1e-5;    %电机的转动惯量[kg*m^2]
Bm = 1e-6;   %电机的粘性扭矩系数[N*s/rad]

% 减速器参数
N = 100; %齿轮数比
E = 0.7; %传递效率

% PID控制参数
Kp =100; %比例增益
Ti =0.1; %积分时间常数
Td =3;   %微分时间常数
eta=0.1; %近似微分参数

3.2 ch6_plot.m函数的编写

新建ch6_plot.m函数，在此函数中绘制单杆的运动轨迹。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% ch6_plot.m
% 第6章 显示结果
%
% Version 1.0 by Hiroumi Mita, CYBERNET SYSTEMS CO.,LTD.
% Version 1.5 by Hongtao Zhang, 2016/08/12 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

close all;

xt=l1*cos(theta);  % x轴上随时间的变化值
yt=l1*sin(theta);  % y轴上随时间的变化值

figure(1)
axis square

for ii=1:length(t)   % 循环，从 ii=1,一直到 ii = length(t)
  x1=[0 xt(ii)];
  y1=[0 yt(ii)];

  h1= line(x1,y1);
  
      if 0<=t(ii)&&t(ii)<=0.5  %加速期间
          set(h1,'color','r');
          set(h1,'lineWidth',2);
      end

      if 0.5<t(ii)&&t(ii)<=2.0  %匀速期间
          set(h1,'color','g');
          set(h1,'lineWidth',2);
      end

      if 2.0<t(ii)&&t(ii)<=2.5  %减速期间
          set(h1,'color','b');
          set(h1,'lineWidth',2);
      end
end

for ii=1:length(t)-1
  x2=[xt(ii) xt(ii+1)];
  y2=[yt(ii) yt(ii+1)];
  h2= line(x2,y2);
  set(h2,'color','k');
  set(h2,'lineWidth',1);
end

% 绘制x轴
h3=line([-0.3 0.3],[0 0]); %给出x轴的数值范围
set(h3,'color','k');
set(h3,'lineWidth',1);

% 绘制y轴
h4=line([0 0],[-0.3 0.3]); %给出y轴的数值范围
set(h4,'color','k');
set(h4,'lineWidth',1);

xlim([-0.3 0.3])
ylim([-0.3 0.3])

4. 运行仿真

1. 首先运行initialize_para.m函数，给仿真系统提供初始化参数
2. 双击仿真系统中的示波器，并运行ch6_sim的仿真
3. 观察到示波器输出如下
   第一幅是运动轨迹函数；第二幅是电机的输入电压，第三幅是单杆侧力矩。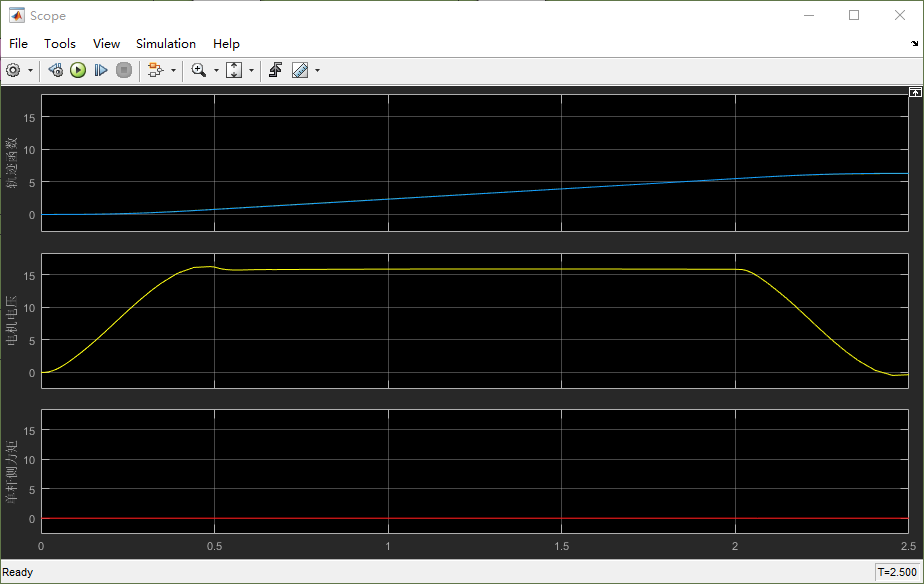
4. 运行ch6_plot.m函数，得到单杆运动轨迹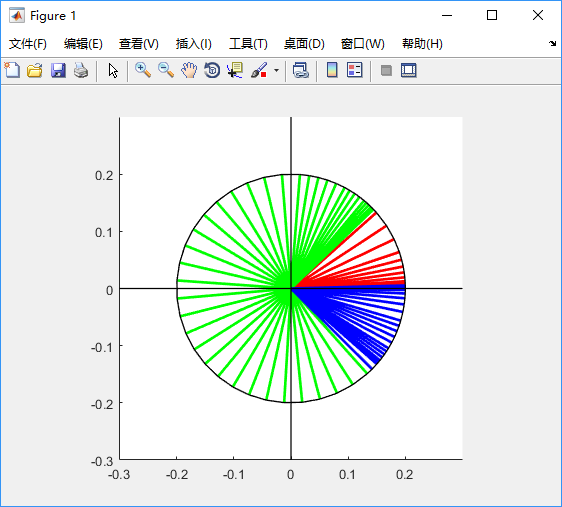

5. 资源下载

感谢《用MATLAB玩转机器人》的作者将此仿真模型提供了完整的资源下载。下载地址即下载教程如下：http://cip.com.cn

最后

以上就是飘逸小蘑菇为你收集整理的用MATLAB玩转机器人--第六章 用MATLAB玩转单关节机器人的全部内容，希望文章能够帮你解决用MATLAB玩转机器人--第六章 用MATLAB玩转单关节机器人所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。