列举组合的所有情况（多层嵌套for循环与递归）

从n个元素中一次抽取m个元素，则共有C(n,m)种可能的情况。那么怎样将组合的所有可能情况一一列举出来呢？
以1至10共10个数字为例

1
2
3
4
5
int array[]=new int[10];
for(int i=0;i<array.length;i++) {
	array[i]=i+1;
}

1. C(10,1)，即从10个数字中抽取1个数字
   我们可以用for循环将其一一列举出来

   复制代码for(int i=0;i<array.length;i++) { System.out.print("["+array[i]+"]"+"t"); }

   1
   2
   3
   4
   for(int i=0;i<array.length;i++) {
   	System.out.print("["+array[i]+"]"+"t");
   }
   

   所有可能情况为：
   

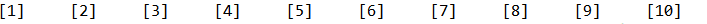
2. C(10,2)，即从10个数字中抽取2个数字
   此时用两层for循环即可将其一一列举出来

   复制代码for(int i=0;i<array.length;i++) { for(int j=i+1;j<array.length;j++) { System.out.print("["+array[i]+"，"+array[j]+"]"+"t"); } System.out.println(); }

   1
   2
   3
   4
   5
   6
   7
   for(int i=0;i<array.length;i++) {
   	for(int j=i+1;j<array.length;j++) {
   		System.out.print("["+array[i]+"，"+array[j]+"]"+"t");
   	}
   	System.out.println();
   }
   

   所有可能情况为：
   

通过以上两个例子就会知道当列举两个数字时，列出的第二个数字是在前一个数字的基础上往后寻找的；那么列举三个数字时，列出的第三个数字是在前二个数字的基础上往后寻找的。所以从n个元素中列举出m个元素，列举出的第m个元素是在前m-1个元素的基础上往后寻找到的，那么要确定前m-1个元素就要确定前m-2个元素，就要确定前m-3个元素……确定前2个元素，确定前1个元素。
所以多层嵌套循环可以帮助我们解决这个问题，列举出m个元素就有m层循环，每一层循环的初始条件是在前一循环初始条件的基础上+1。

3. C(10,5)，即从10个数字中抽取5个数字
   此时要用到5层for循环，代码特别繁杂

   复制代码int count=0; for(int i=0;i<array.length;i++) { for(int j=i+1;j<array.length;j++) { for(int k=j+1;k<array.length;k++) { for(int m=k+1;m<array.length;m++) { for(int n=m+1;n<array.length;n++) { System.out.print("["+array[i]+"，"+array[j]+"，"+array[k]+"，"+array[m]+"，"+array[n]+"]"+"t"); count++; } } } } System.out.println("_____"); } System.out.println("共枚举出"+count+"种组合");

   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   int count=0;
   for(int i=0;i<array.length;i++) {
   	for(int j=i+1;j<array.length;j++) {
   		for(int k=j+1;k<array.length;k++) {
   			for(int m=k+1;m<array.length;m++) {
   				for(int n=m+1;n<array.length;n++) {
   					System.out.print("["+array[i]+"，"+array[j]+"，"+array[k]+"，"+array[m]+"，"+array[n]+"]"+"t");
   					count++;
   				}
   			}
   			
   		}
   		
   	}
   	System.out.println("_____");
   }
   
   System.out.println("共枚举出"+count+"种组合");
   

   所有可能情况为：
   
   因结果较长，未截取所有情况。

如果要列举出的元素个数特别大，那么多层嵌套循环显然不适合解决该类问题。而递归能够实现多层嵌套循环且代码足够简洁。

代码于下
public class Enumerate {

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int array[]= {1,2,3,4,5,6,7,8,9,10};
int temp[]=new int[5];//记录依次抽取到的5个数字的下标
int count=0;//统计组合的情况总数

public void method(int i,int j) {//递归方法
	i++;//确定第i层循环
	for(int k=j;k<array.length;k++) {
		temp[i-1]=k;//每一层循环都将抽取一个数字，记录其下标
		
		if(i!=5) {//深入到下一层循环
			j++;//在前一循环初始条件的基础上+1
			method(i,j);
		}else {//已经在第5层循环
			count++;
			System.out.println("["+array[temp[0]]+"，"+array[temp[1]]+"，"+array[temp[2]]+"，"+array[temp[3]]+"，"+array[temp[4]]+"]"+"t");
		}
	}//结束for循环
	
}//结束method方法

public static void main(String[] args) {
	Enumerate obj=new Enumerate();
	obj.method(0,0);
	System.out.println("共枚举出"+obj.count+"种组合");
}//结束main方法

}//结束Enumerate类

运行结果为

因结果较长，未截取所有情况。

最后

以上就是威武流沙最近收集整理的关于列举组合的所有情况（多层嵌套for循环与递归）的全部内容，更多相关列举组合内容请搜索靠谱客的其他文章。