前言

在Monte Carlo模拟技术中，许多地方都需要用到符合标准正态分布(高斯)的随机数来设计采样方案，因此了解如何用均匀分布随机数(实际上是均匀分布的伪随机数)来生成标准正态分布的随机数十分重要。本文将对这个最基本的问题做讨论，并提供c++11代码。

在讨论更高效的算法之前，我们先来看看能不能基于中心极限定理来设计算法。中心极限定理告诉我们，对于一组$i.i.d$的随机数 { x k } ∼ U ( μ , σ 2 ) {x_k}sim U(mu,sigma^2) {xk​}∼U(μ,σ2)，有$\frac{1}{n}{\sum }_{i=1}^n{x}_i\to N(\mu ,{\sigma }^2/n)$。这个算法有两个问题：

1. 计算量大。生成一个数需要用n个均匀分布随机数。
2. 无法准确刻画正态分布的末端效应。生成的数均有界，不会是很大的数。

此外，如果用“拒绝采样(rejection sampling)“的思路，在覆盖$f(x)=c{e}^{-x^2/2}$的矩形内均匀投点，保留曲线下的点，则计算较复杂(exp函数)，而且舍弃点多代价大。

我们下面介绍两种更高效的算法：The Box–Muller transform 和 The Ziggurat algorithm。它们一个是对分布函数做了变换，另一个还是使用了“拒绝采样“的思路，但并不是简单的仅用一个大矩形覆盖。

The Box–Muller transform

The Box–Muller transform 把一对均匀分布随机数映射到一对标准正态分布随机数。它有两种形式：

1. 基本形式：用$(0,1)$均匀分布随机数，需要计算三角函数$\sin$和$\cos$；
2. 极坐标形式：用$(-1,1)$均匀分布随机数，且不需要计算三角函数。

我们希望计算积分$I={\int }_{-\infty }^{\infty }{e}^{-x^2/2}dx$，可以先取它的平方并用极坐标表示，$$I^2={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{e}^{-(x^2+y^2)/2}dxdy={\int }_0^{2\pi }{\int }_0^{\infty }r{e}^{r^2/2}drd\theta .$$可以看到极角$\theta$服从$(0,2\pi )$均匀分布，径向距离$r$服从$r{e}^{r^2/2}$分布函数(即$r^2$服从${\chi }^2分布$)。如果把$r$的累积分布函数(cumulative distribution function)写出来$$F(x)={\int }_0^{x}r{e}^{r^2/2}dr=1-e^{-x^2/2},$$我们就可以通过$F$的逆函数$F^{-1}(u)$，将均匀分布$u\sim U(0,1)$映射到目标分布，即$x=\sqrt{-2\ln (1-u)}$，也等价于$x=\sqrt{-2\ln u}$ (注意到如果$u\sim U(0,1)$，那么$1-u$也是)。

基本形式：
假设$U_1$和$U_2$是区间$(0,1)$上的均匀分布随机数，令
$Z_1=R\cos (\theta )=\sqrt{-2\ln U_1}\cos (2\pi U_2)$，
$Z_2=R\sin (\theta )=\sqrt{-2\ln U_1}\sin (2\pi U_2)$，
则$Z_1$和$Z_2$是两个独立的标准正态分布随机变量。

极坐标形式：
转换到极坐标的方法叫做Marsaglia polar method。该方法对水平和竖直方向$(-1,1)$正方形区域内均匀投点，把落在单位圆内的点$(x,y)$通过$s=x^2+y^2$映射到单位圆周上，即$(\frac{x}{\sqrt{s}},\frac{y}{\sqrt{s}})$，这样就可以不用计算三角函数。由于$s\equiv r^2$独立于极角，且在区间$(0,1)$上均匀分布（因为$\int \int dxdy=\int \int rdrd\theta =\int \int \frac{1}{2}d{r}^{2}d\theta$），因此可以用这个$s$继续得到径向距离$\sqrt{-2\ln (s)}$。于是我们有：
$Z_1=\sqrt{-2\ln U_1}\cos (2\pi U_2)=\sqrt{-2\ln s}\left(\frac{u}{\sqrt{s}}\right)=u\cdot \sqrt{\frac{-2\ln s}{s}},$
$Z_2=\sqrt{-2\ln U_1}\sin (2\pi U_2)=\sqrt{-2\ln s}\left(\frac{v}{\sqrt{s}}\right)=v\cdot \sqrt{\frac{-2\ln s}{s}}.$
极坐标形式对应的c++代码如下（顺带说一下，c++标准函数库libstdc++里std::normal_distribution用的就是Marsaglia polar method，见这里）：

//
// Marsaglia polar method. C++11 代码
// 由于生成的是一对i.i.d.高斯变量，每次生成的两个样本都可以利用起来！
//
bool _M_saved_available=false;
if (_M_saved_available) //输出下面暂时储存的x*mult
{
    _M_saved_available = false;
    return = _M_saved;
}
else
{
    double x, y, r2;
    do
    {
        x = 2.0 * rand() - 1.0;
        y = 2.0 * rand() - 1.0;
        r2 = x * x + y * y;
    }
    while (r2 > 1.0 || r2 == 0.0);
    
    const double mult = std::sqrt(-2 * std::log(r2) / r2);
    _M_saved = x * mult;
    _M_saved_available = true; //暂时储存x*mult，输出y*mult
    return = y * mult;
}

算法局限性： 尾部截断(Tails truncation)
由于计算机有数值精度限制，其表示的数字不可能无线接近0。比如，使用32bit精度，那么最接近0的数字是$2^{-32}$。因此，当$u_1$和$u_2$都取$2^{-32}$时，$x$的最大值是$\sqrt{-2\ln (2^{-32})}\cos (2^{-32})\approx 6.6$，即产生的随机数最大不会超过$6.6$个标准差，这意味着会有$2\times 10^{-11}$的比例(尾部)会因为计算机精度问题无法采样到，这在大规模生成高斯随机数和研究rare events的时候要特别注意。

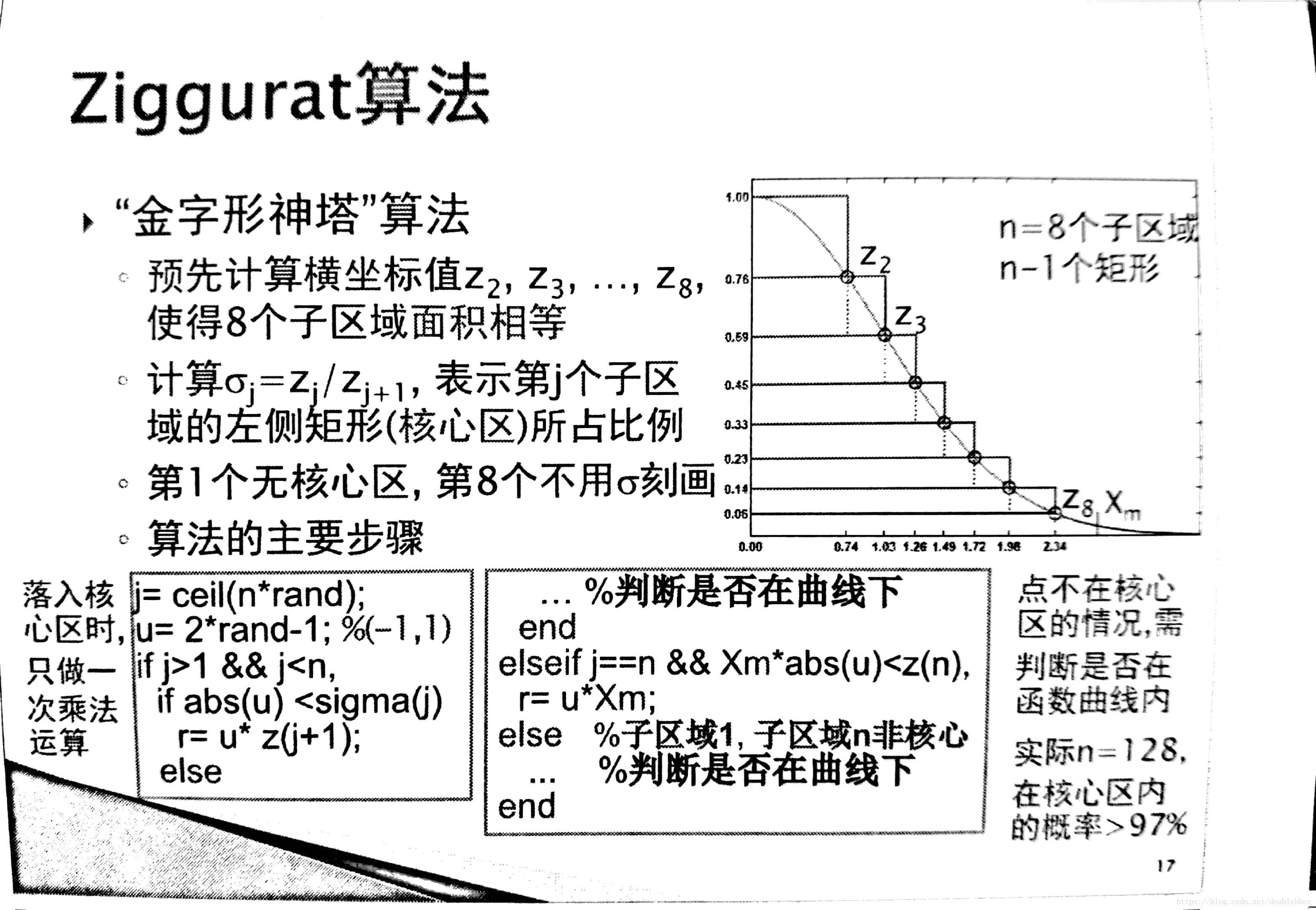
The Ziggurat algorithm(金字形神塔)

The Ziggurat algorithm 属于rejection sampling的一种。这个方法适用于分布函数是单调递减的情况，而正态分布的正半轴就属于这种情况。

附录：Inverse transform sampling直观解释

数学解释： 假设$F(x)=Pr[X<x]$是CDF，并假设$u\sim U(0,1)$，定义映射$X=f(x)$，这个映射是$[0,1]\to R$。我们希望找到一个映射使得$X$恰好服从$F(x)$的CDF分布，即$Pr[f(U)<x]=F(x)$。显然，$f=F^{-1}$，因为$Pr[X<x]=Pr[f(u)<x]=Pr[u<F(x)]=F(x)$。

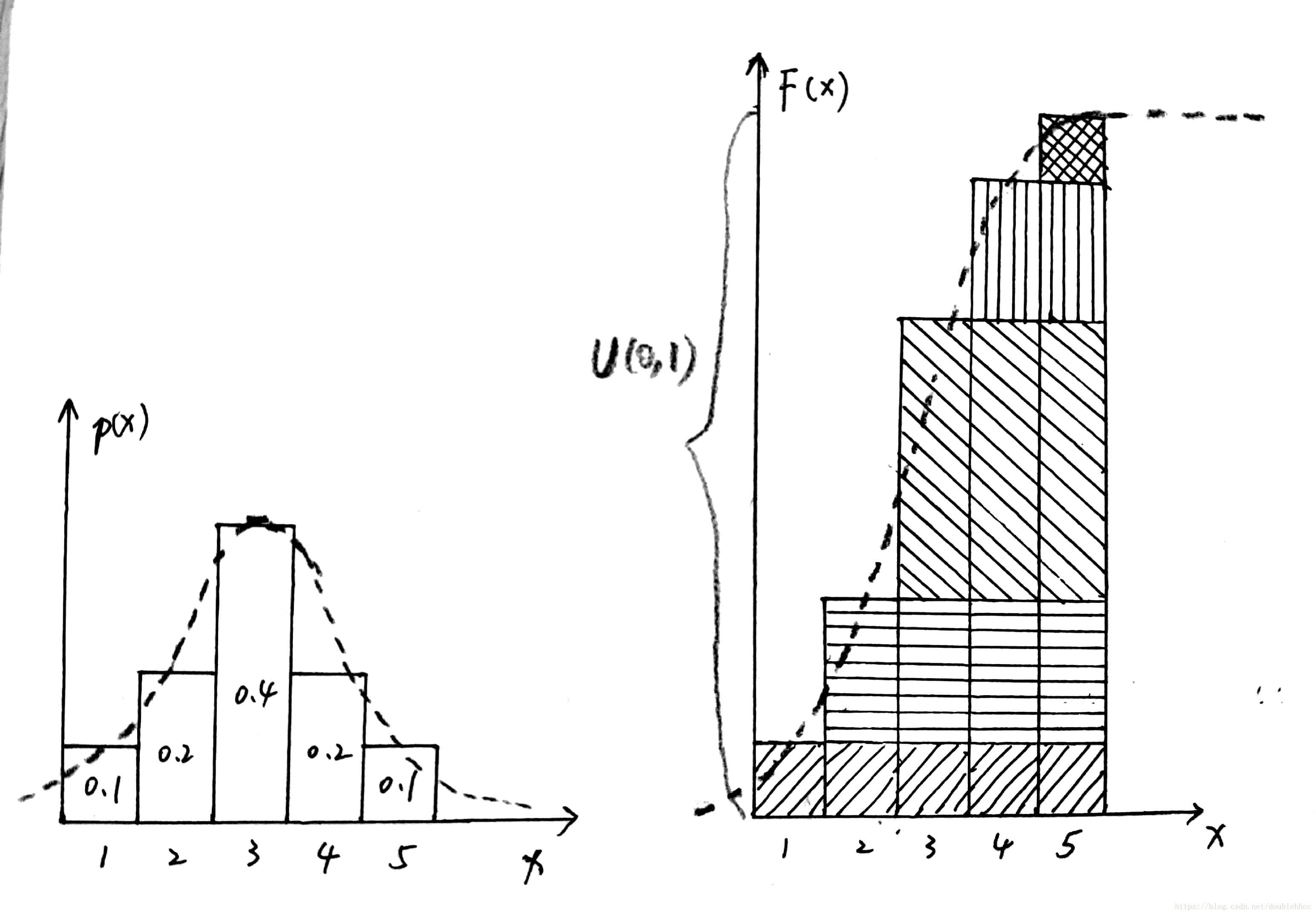
图像解释： 我们假设随机变量取值是离散的，比如一共有5种取值。右边是CDF，相当于把左边的概率“盒子“逐渐堆积起来，直到最后一列对应的$F$正好等于1。这时候对$F(x)$均匀采样的话，相当于在最后一列按照各个盒子面积的相对大小（各部分的概率大小）来采样，$F(x)$的逆函数只是用来回溯到对应的$x$而已。随机变量取连续情况同样适用上述论证过程。

[1]:
[2]: https://github.com/jmcmanus/pagedown-extra “Pagedown Extra”
[3]: http://meta.math.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference
[4]: http://bramp.github.io/js-sequence-diagrams/
[5]: http://adrai.github.io/flowchart.js/
[6]: https://github.com/benweet/stackedit

最后

以上就是谨慎巨人最近收集整理的关于如何用均匀分布随机数生成正态分布随机数前言The Box–Muller transformThe Ziggurat algorithm(金字形神塔)附录：Inverse transform sampling直观解释的全部内容，更多相关如何用均匀分布随机数生成正态分布随机数前言The内容请搜索靠谱客的其他文章。