信号检测、估计和通信等问题都需要经仿真进行性能分析，产生服从特定分布的随机变量至关重要。

MATLAB中提供了现成的函数random，可以产生服从某种确定分布的随机序列。还有一些其它函数，比如exprnd专门用于产生服从指数分布的随机序列，但总体上random要更为通用。

我们平时只管调用函数即可，简化工作量，而无需关心random函数背后的计算原理。最近学习的《信号检测与估计-理论与应用》简单介绍了一下相关部分。在此做个记录。

1.指数分布随机序列

总的来说，想生成一个服从某确定分布随机变量的一般方法，是先产生[0,1]区间内均匀分布的随机变量U，经过如下变换
$$X={F_x}^{-1}(U)$$
即可产生满足分布函数F_X (x)的随机变量X的随机序列。如参数为1的指数分布随机变量的概率密度函数和分布函数为：
$$P_X(x)=e^{-x},x\ge 0$$
$$F_X(x)=1-e^{(}-x),x\ge 0$$
由F_X (x)的反函数得到：
$$X=-ln(1-U)$$
由于U服从均匀分布时，1-U也服从均匀分布，因此上式可简化为：
$$X=-ln(U)$$
设计MATLAB程序如下（R2017a版本下编写），rand函数产生均匀分布的序列。各个函数的具体用法一定要在Help中搜索，没必要在博客里细说。如果经常用MATLAB做仿真，而不是为了应付几次作业，一定要养成查看help文档的习惯。：

%-------------------------------------------------
%            计算产生指数分布随机序列
%-------------------------------------------------
clc; clear; close all;
 
num = 10000;           % 数据长度
n10=num/10;
u = rand(num,1);       % 产生均匀分布序列
 
x = 0:.1:10;
z = -log(u);           % 得到指数分布序列
et = hist(z,x);        % 计算概率密度函数
nznorm = et/n10;       % 归一化
Ex = mean(z); Dx = var(z);  % 计算统计量
plot(x,nznorm,'b'); title('计算方式-指数分布随机变量，Ex='...
    +string(Ex)+'，Dx='+string(Dx));
xlabel('x'); ylabel('p_X (x)');
grid on; hold on
y=exp(-x);
plot(x,y,'m')
legend('模拟数据曲线','理论曲线');
 
figure;
%z = exprnd(1,num,1);
z = random('exp',1,[num,1]);
et = hist(z,x);
nznorm = et/n10;       % 归一化
Ex = mean(z); Dx = var(z);  % 计算统计量
plot(x,nznorm,'b'); title('exprnd函数-指数分布随机变量，Ex='...
    +string(Ex)+'，Dx='+string(Dx));
xlabel('x'); ylabel('p_X (x)'); grid on;

计算方式生成的随机序列的概率密度函数，与标准指数分布概率密度函数公式的对比如下图。样本点数量num越大，则两者越接近。

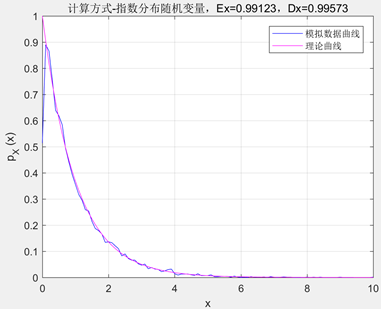
使用random函数产生指数分布随机序列，概率密度函数如下

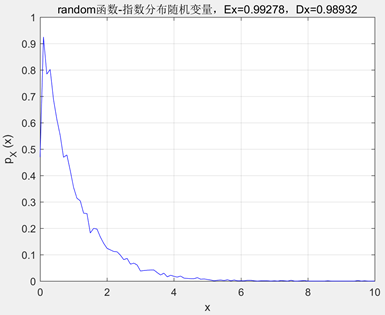
指数分布的参数λ为1。计算方式产生的序列数学期望为0.99123，方差为0.99573；random函数产生的序列数学期望为0.99278，方差为0.98932。两者都有不错的性能，和真实参数非常接近（对于指数分布，E(x)=D(x)=λ）。

概率密度函数的计算采用了直方图计算的方式（hist函数），直方图绘制的是所有数据在各个区间内的个数。从离散化的角度来看概率密度函数，意义和直方图一模一样。

无论是MATLAB还是哪种编程语言中，所有基于连续方式定义的公式都要将变量离散化。最简单的例子大家都接触过，用MALLAB绘制一个sin(t)函数，就要先根据采样频率生成离散的时间序列t。

如何将书本、论文中的公式转换为编程语言，是必备技能。本科阶段或许还不是很重视这方面的技能提升，但研究生阶段不会这个连算法都没法仿真，论文都没法写。所以要多加练习，多看代码。

2.正态分布随机变量

random函数也可以生成正态分布的随机序列。下面介绍两种计算方法。

2.1 中心极限定理

假定一个随机变量X是多个独立随机变量之和，在满足一定条件时，随机变量逼近正态分布。一般可以采用m个独立的均匀分布随机变量相加得到X，则X服从均值为m/2、方差为m/12的正态分布。有需要也可以根据概率论知识将生成的序列标准化，得到标准正态分布。

MATLAB设计程序如下（R2017a版本下编写）：

%-------------------------------------------------
%            计算产生正态分布随机变量
%-------------------------------------------------
clc; clear; close all;
 
m = 100;              % 序列数目
num = 1000;           % 单个序列的数据长度
 
x = zeros(1,1000);
for i = 1 : m
    u = rand(1,num);       % 产生均匀分布序列
    x = x + u;
end
 
xax=[min(x):.1:max(x)];
nx=hist(x,xax);
plot(xax,nx); title('中心极限定理 num='+string(num));

rand函数产生均匀分布的随机序列，叠加m=100个序列，则理论上的数学期望为m/2=50，方差为m/12=8.33。单个序列的长度num将极大影响到生成随机序列的质量。下面给出不同num下的测试结果。

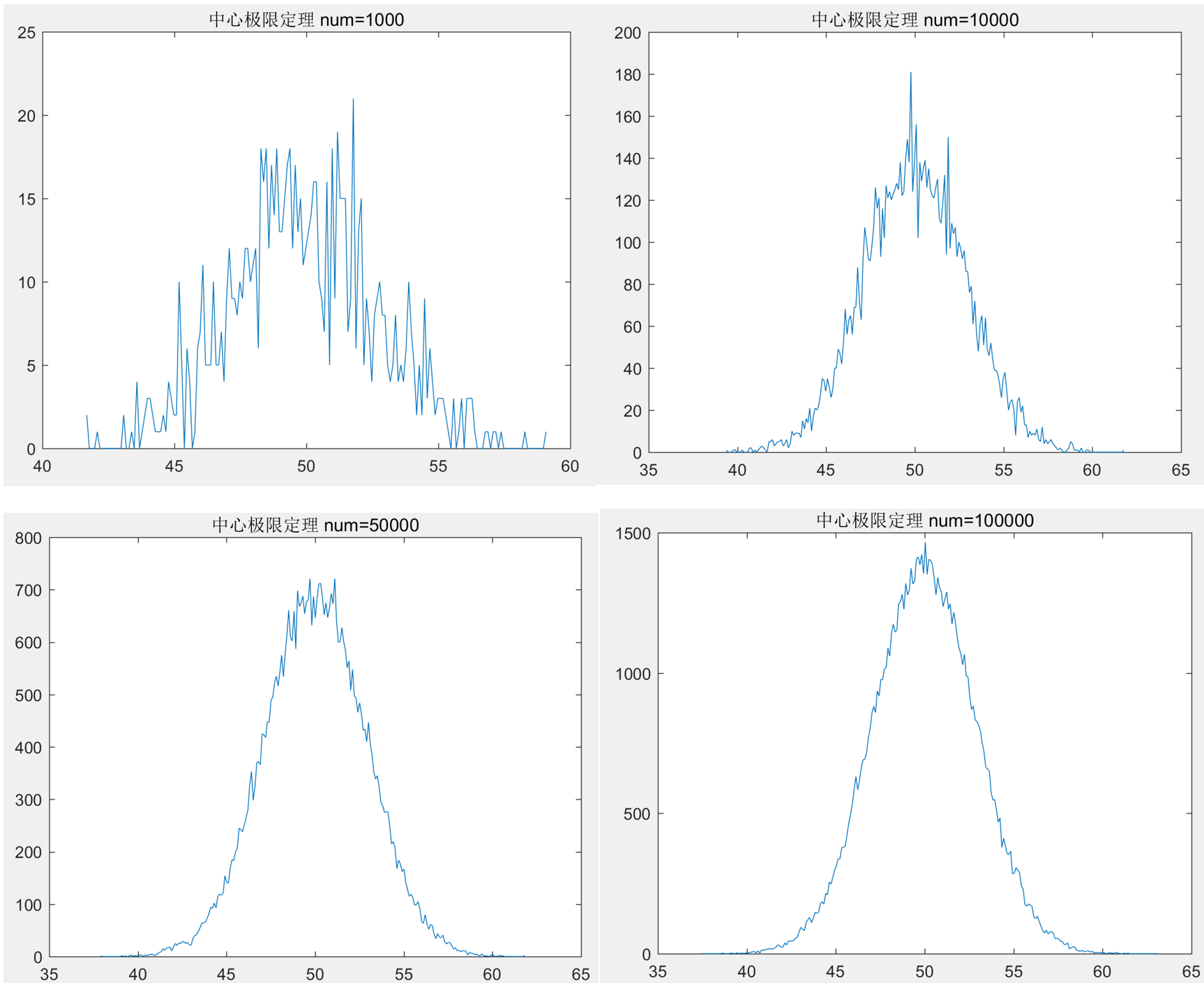
显而易见，num越大，叠加序列越接近于服从正态分布的随机序列。

2.2 联合正态分布

利用中心极限定理生成正态分布随机序列，显而易见的弊端就是数据量太大。本节介绍的方法利用log函数和三角函数产生独立的高斯随机变量对。假设U_1和U_2是两个0到1之间的均匀分布。定义：
$$X=\sqrt{(-2ln{U}_1)}cos(2\pi U_2)$$
$$Y=\sqrt{(-2ln{U}_1)}sin(2\pi U_2)$$
则随机变量X、Y服从数学期望为0、方差为1的联合正态分布。设计MATLAB程序如下（R2017a版本下编写）：

%-------------------------------------------------
%            计算产生正态分布随机变量
%-------------------------------------------------
clc; clear; close all;
num = 100000;
 
ui = rand(1,num);
uq = rand(1,num);
x = zeros(1,num);
y = zeros(1,num);
for i=1:num
   x(i)=((-2.*log(ui(i)))^.5)*cos(2*pi*uq(i));
   y(i)=((-2.*log(ui(i)))^.5)*sin(2*pi*uq(i));
end
 
xax=[-5:.1:5];
yax=[-5:.1:5];
nx=hist(x,xax);
ny=hist(y,yax);
 
p=nx'*ny;
mesh(xax,yax,p)
hold on
xlabel('x'); ylabel('y');
zlabel('p_X_Y(x,y)')

结果如下图：

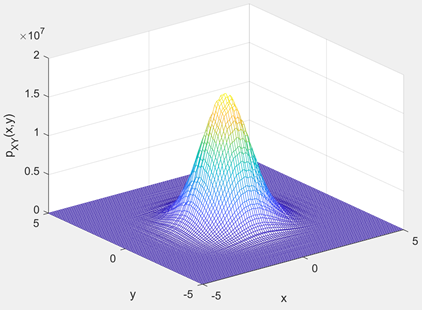
今天看书时，对这块比较感兴趣，就结合《信号检测与估计-理论与应用》第二版中文版p18-p21的内容，结合这本书的源程序实现了一下。当然实际中我们不会用这么复杂的方法产生随机序列，直接用random函数就行了。

我对理论类书籍中用代码实现的部分都比较感兴趣。我相信只有锻炼多了，做自己的算法仿真时才能得心应手。

最后

以上就是忧虑茉莉为你收集整理的MATLAB数字信号处理（3）计算方式生成随机序列1.指数分布随机序列2.正态分布随机变量的全部内容，希望文章能够帮你解决MATLAB数字信号处理（3）计算方式生成随机序列1.指数分布随机序列2.正态分布随机变量所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。