因式分解
行列式、逆、秩
- det(A) 行列式
- rank(A) 矩阵A的秩
- inv(A) 矩阵A的逆矩阵,非方针和奇异矩阵(不是满秩的矩阵)会报错
- pinv(A) 求A的伪逆矩阵,是逆矩阵的广义化。
- trance(A) 求矩阵A的迹,就是对角线元素之和
伴随矩阵求法:
A* = compan(B)
A* = inv(A) * det(A)
Cholesky 因式分解
正定矩阵定义:A是n阶方阵,如果对任何非零向量x,都有xTAx>0,其中xT 表示x的转置,就称A正定矩阵。
Cholesky 因式分解是将A分解为一个上三角矩阵R和其转置矩阵的乘积。对应表达式:
A = R’R
条件:正定矩阵
>> a = pascal(6)%初始化
>> R = chol(a)
R =
1 1 1 1 1 1
0 1 2 3 4 5
0 0 1 3 6 10
0 0 0 1 4 10
0 0 0 0 1 5
0 0 0 0 0 1
>> R'* R == a%证明其等价关系
ans =
6×6 logical 数组
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
LU因式分解
LU分解用于简化大矩阵行列式的计算过程、矩阵求逆和连立方程组的求解
注意:结果不唯一
调用:
[L,U] = lu(A)
对于Ax = b的求解
x = U(Lb)
‘’是左除符号,左除左边的矩阵
验证:
>> a = pascal(3)
a =
1 1 1
1 2 3
1 3 6
>> [L U] = lu(a)
L =
1.0000 0 0
1.0000 0.5000 1.0000
1.0000 1.0000 0
U =
1.0000 1.0000 1.0000
0 2.0000 5.0000
0 0 -0.5000
>> L * U
ans =
1 1 1
1 2 3
1 3 6
QR因式分解
若A为正交矩阵,则A’A = 1
QR分解即为正交分解,将A分为一个单位正交矩阵和上三角矩阵
A = QR
验证
>> a = magic(3)
a =
8 1 6
3 5 7
4 9 2
>> [Q R] = qr(a)
Q =
-0.8480 0.5223 0.0901
-0.3180 -0.3655 -0.8748
-0.4240 -0.7705 0.4760
R =
-9.4340 -6.2540 -8.1620
0 -8.2394 -0.9655
0 0 -4.6314
>> Q * R
ans =
8.0000 1.0000 6.0000
3.0000 5.0000 7.0000
4.0000 9.0000 2.0000
>>
范数
范数是一个标量,用来衡量向量的长度。
范数 != 向量的元素个数
| 函数 | 含义 | 数学含义 |
|---|---|---|
| norm(X) | 欧几里得范数 | 根号下xk绝对值的平方和 |
| norm(X,inf) | 求♾范数 | x绝对值最大值 |
| norm(X,1) | 求1范数 | xk绝对值的和 |
| norm(x,p) | p范数 | p可以是任意值 |
>> x = [2 4 5]
x =
2 4 5
>> norm1 = norm(x)
norm1 =
6.7082
>> norm2 = norm(x,1)
norm2 =
11
>> norm3 = norm(x,inf)
norm3 =
5
>> norm4 = norm(x,4)
norm4 =
5.4727
矩阵的特征值和奇异值
E = eig(A) 求出A的全部特征值,构成向量E
[V,D] = eig(A)求出A的全部特征值,构成D,特征向量,构成V
>> A = [1,-3;2,2/3]
A =
1.0000 -3.0000
2.0000 0.6667
>> [V,D] = eig(A)
V =
0.7746 + 0.0000i 0.7746 + 0.0000i
0.0430 - 0.6310i 0.0430 + 0.6310i
D =
0.8333 + 2.4438i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.8333 - 2.4438i
求解x4 -2x3 +3x2 +4x-5 = 0 的根
思路:伴随矩阵的特征根即为方程的根。
>> B = [1,-2,3,4,-5]
B =
1 -2 3 4 -5
>> A = compan(B)
A =
2 -3 -4 5
1 0 0 0
0 1 0 0
0 0 1 0
>> C = eig(A)
C =
1.1641 + 1.8573i
1.1641 - 1.8573i
-1.1973 + 0.0000i
0.8691 + 0.0000i
奇异值
如果存在两个矢量
u
,
v
u,v
u,v以及一个常数
s
s
s使得矩阵A满足
A
v
=
s
u
Av = su
Av=su
A
′
u
=
s
v
A'u = sv
A′u=sv
则称
s
s
s为奇异值,
u
,
v
u,v
u,v为奇异矢量.
奇异值分解是一种正交矩阵分解法
调用
[U,S,V] = svd(A)
A = U * S * V’
概率与数理统计
sum函数,和
用于求矩阵列向量的和
B = sum(A) 若A为向量,返回元素和,若A为矩阵,返回列向量和(存放在一个行向量中)
B = sum(A,dim) 对dim维度求和
comsum函数,累计和
B = comsum(A) 同上,返回的是一个加和,
B = comcum(A,dim)同上
prod函数,积
B = prod(A) 如果A是向量,返回所有元素的积,如果A是矩阵,返回各列元素的积
B = prod(A,dim) 同上。
comprod 函数,累积
同上
sort函数
B = sort(A)对A进行默认升序排序。输入A可以是向量、矩阵和字符串
B = sort(A,dim) 对第dim维度进行升序排列
B = sort(…,mode) mode是升序降序’ascend’ ‘descend’
[B,IX] = sort(A,2) 排序并且返回下标
sortrows函数
B = sortrows(A) 对A进行升序排列
B = sortrows(A,column) 基于column列进行升序排列
[B,index] = sortrows(A…) 同时返回索引表
max和min函数
max(A) 如果是向量 返回最大的元素,如果是矩阵,返回列向量最大
max(A,B) 返回每个元素为止A,B的大的那个
[C,I] = max() 同时返回下标
max(A,[],dim)返回A中dim维度的最大值,1 是列2 是行
mean 函数
M = mean(A) 求平均值
M = mean(A,dim)
median函数
求中值
median(A)
median(A,dim)
std函数
标准差
(1)
s
=
⟮
1
n
−
1
∑
i
=
1
n
(
x
−
x
ˉ
)
2
⟯
1
2
s =lgroup frac{1}{n-1}sum_{i = 1}^{n}{(x-bar{x})}^2rgroup^frac{1}{2}tag{1}
s=⟮n−11i=1∑n(x−xˉ)2⟯21(1)
(2)
s
=
⟮
1
n
∑
i
=
1
n
(
x
−
x
ˉ
)
2
⟯
1
2
s =lgroup frac{1}{n}sum_{i = 1}^{n}{(x-bar{x})}^2rgroup^frac{1}{2}tag{2}
s=⟮n1i=1∑n(x−xˉ)2⟯21(2)
(3)
x
ˉ
=
1
n
∑
i
=
1
n
x
i
bar{x} = frac{1}{n}sum_{i = 1}^{n}x_{i}tag{3}
xˉ=n1i=1∑nxi(3)
调用:
s = std(x) 计算样本的标准差,计算式(1)计算标准差
s = std(x, flag) flag = 0 同上 flag =1 用(2)的方式求方差
s = std(x,flag,dim) 返回第dim维度的标准差
var函数
求方差
V = var(X) 若X为向量,计算X方差,若X为矩阵,计算列方差
V = (X,1) 按照(2)计算方差
V= var(X,w,dim)dim维度方差,权重向量w计算
cov函数
协方差矩阵计算函数
c
o
v
(
x
1
,
x
2
)
=
E
[
(
x
1
−
u
1
)
(
x
2
−
u
2
)
]
cov(x_1,x_2) = E[(x_1 - u_1)(x_2 - u_2)]
cov(x1,x2)=E[(x1−u1)(x2−u2)]
u
1
=
E
(
x
1
)
u_1 = E(x_1)
u1=E(x1)
u
2
=
E
(
x
2
)
u_2 = E(x_2)
u2=E(x2)
协方差主要说的是两个随机量的差别
C = cov(x) 若x为向量,返回的是向量的方差,若x是矩阵,返回协方差矩阵
cov(x,y) x列y列的协方差
corrcoef函数
求相关系数
ρ
x
y
rho_{xy}
ρxy
ρ
x
y
=
c
o
v
(
X
,
Y
)
D
(
X
)
D
(
Y
)
rho_{xy} = frac{cov(X,Y)}{sqrt{D(X)}sqrt{D(Y)}}
ρxy=D(X)D(Y)cov(X,Y)
corrcoef(x) 若X为矩阵,返回一个相关系数矩阵
corrcoef(x,y) 返回数值,x和y列的相关系数
概率密度、分布函数、逆分布函数、随机数
逆分布函数 = 逆累积分布函数 = 分布函数的反函数
用处:输入参数0.9可以查到当累积到
X
=
x
i
X = x_{i}
X=xi的时候置信区间为0.9,即
P
(
X
<
x
i
)
=
0.9
P_{(X<x_{i})} = 0.9
P(X<xi)=0.9,返回这个
x
i
x_{i}
xi
| 分布名称 | 概率密度函数 | 累积分布函数 | 逆累积分布函数 | 随机发生器 |
|---|---|---|---|---|
| 二项分布 | binopdf | binocdf | binoinv | binornd |
| 柏松分布 | poisspdf | poisssdf | poissinv | poissrnd |
| 正态分布 | normpdf | normcdf | norminv | normrnd |
| 均匀分布 | unifpdf | unifcdf | unifinv | unifrnd |
| χ 2 chi^{2} χ2分布 | chi2pdf | chi2cdf | chi2inv | chi2rnd |
| F分布 | fpdf | fcdf | finv | frnd |
| t分布 | tpdf | tcdf | tinv | trnd |
实例:
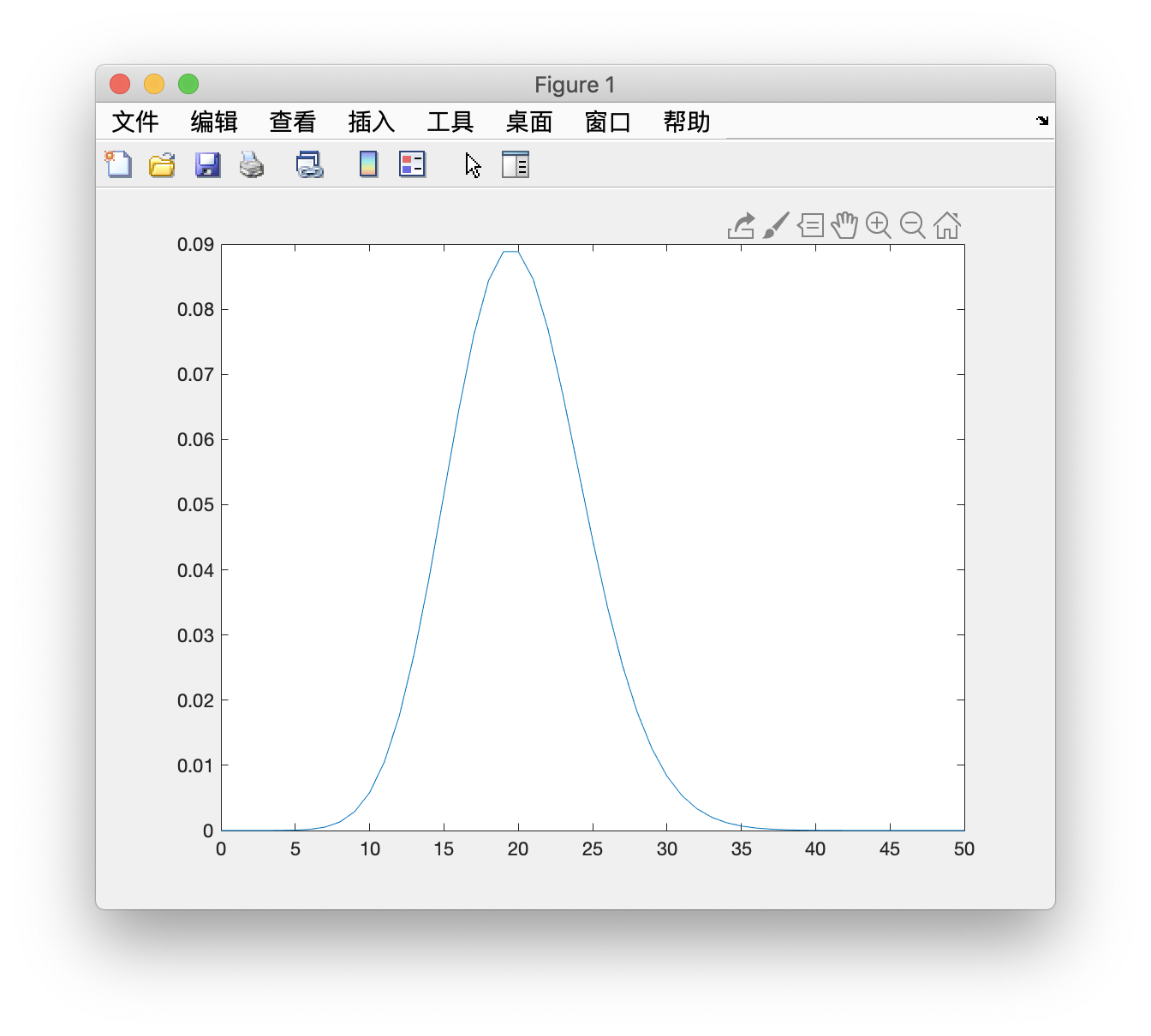
参数为20的泊松分布概率密度函数
>> x = 0:50;
>> Lamada = 20;
>> r = poisspdf(x,Lamada);
>> plot(x,r)
最后
以上就是冷静薯片最近收集整理的关于MATLAB学习笔记(六) 因式分解、概率与数理统计因式分解矩阵的特征值和奇异值概率与数理统计的全部内容,更多相关MATLAB学习笔记(六)内容请搜索靠谱客的其他文章。

![triplus在matlab字函数,[理学]第7章 MATLAB在信号处理中的应用.ppt](https://www.shuijiaxian.com/files_image/reation/bcimg3.png)






发表评论 取消回复