目录
逻辑代数
逻辑变量与逻辑常量
基本逻辑运算
与
或
非
常用组合逻辑运算
与非:
或非:
与或非:
异或:
同或:
逻辑代数基本定理
1.代入定理
2.反演定理
3.对偶定理
逻辑运算公式
逻辑函数的化简
最小项
公式化简法
卡诺图化简法
无关项:
逻辑代数
布尔代数也称为逻辑代数。但是数字电路中信号分析运算只涉及到布尔代数的一部分。也就是说,布尔代数是进行电路分析运算的数学工具。所谓逻辑,就是事物的因果关系。逻辑函数简单理解就是从原因到结果的一个映射。
逻辑变量与逻辑常量
逻辑变量是逻辑代数中使用字母表示的变量。比如普通代数中函数 y = kx + b,就是使用字母来表示变量的。函数式表达了一个变量y与变量k、x、b之间的关系。逻辑函数 y = kx + b 同样表示的是这些变量之间的关系。
不同之处在于,逻辑变量只有0和1两种取值。也就是说,逻辑代数中出现的常量只有0和1。我们称0和1是逻辑常量。比如上面的函数式,如果k是一个常量,那么在普通代数中,它可以取任意的值,但是在逻辑代数中它只能取01。
基本逻辑运算
与
所有同时具备,结果发生。记作Y = A AND B = A & B = A·B = AB
逻辑门画法:(手绘轻喷)
![]()
真值表:
| 输入A | 输入B | 输出Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
或
条件之一具备,结果发生。记作 Y = A OR B = A + B
逻辑门画法:
![]()
真值表:
| 输入A | 输入B | 输出Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
非
条件不具备,结果发生。记作Y = NOT A = Ā = A'
逻辑门画法:
![]()
值得一提的是,不管三角形还是方框,都只是为了形式上更好看。后面的圈才是非门的主体。这个圈加在什么地方,就相当于在这里加一个非门。(在后面符合逻辑中会有例子)
真值表:
| 输入A | 输出Y |
| 0 | 1 |
| 1 | 0 |
常用组合逻辑运算
与非:
就是对与的结果取非。画电路图时,非门可以缩成一个圈附在与门后面,表示一个整体,是与非门
![]()
(鉴于教科书采用的这一套有特殊形状的表示符,因此后面只展示这一种画法了)
或非:
![]()
就是对或的结果取非。
与或非:
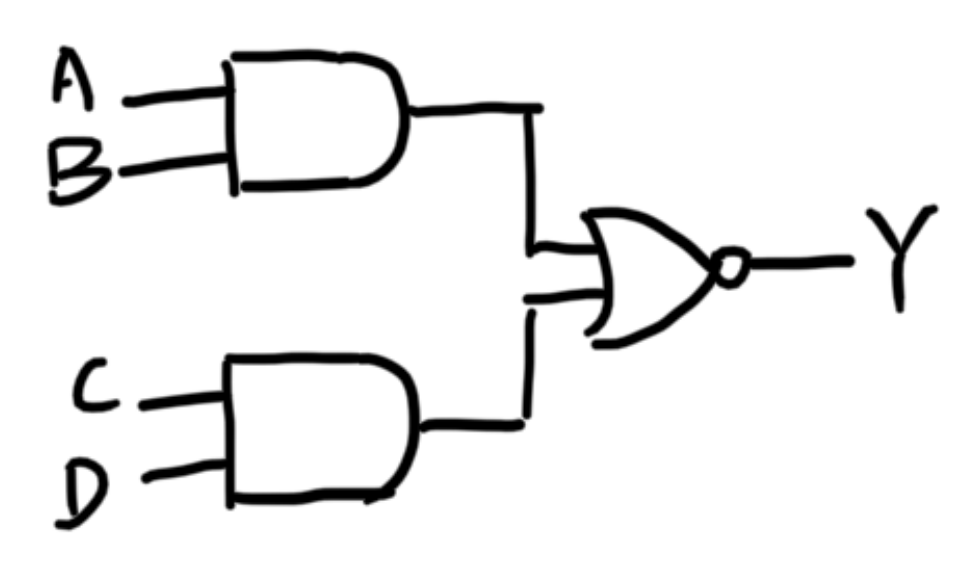
先取与,再对结果取或,再取非。
现在一定要熟悉这样一种结构。每一次运算都要通过门电路来实现,不能仅凭电路知识想当然。在未来会遭遇“线与”,如果处理不当是会出问题的(烧板子)。
异或:
![]()
首先从名字上来理解这个运算:对相异的取或。它的表达式也确实是这样:Y = A'B + AB'
直观的看就是当两个变量的输入不同时输出为1。也就是相异时出1。
同或:
![]()
同样从名字上理解就是对相同的取或。Y = AB + A'B'
由后面将要讲到的摩根定理可以知道,同或=异或取非(在后面会有证明过程)
逻辑代数基本定理
1.代入定理
直观理解就是画框定理。对式子中任何一个变量画框,然后在框里面装上一切你想要装的东西。这里可以联想一下C语言编程的宏。我们把A定义成一个宏,虽然运算的时候写Y=A+B,但是A里面装什么内容其实是可以替换的。这里要注意代入定理的适用范围:逻辑等式
2.反演定理
加乘互换,0 1 互换,原反互换
也就是或运算和与运算互换,常量的0 和1 互换,所有逻辑变量全部取反。
使用反演定理可以方便的求出一个逻辑函数的反函数:
Y = A(B + C) + CD
Y1=(A+BC)(C+D) ……加乘、01互换
Y2=(A'+B'C')(C'+D') ……所有变量全部取反
Y'=A'C'+A'D'+B'C'+B'C'D'=A'C'+A'D'+B'C'
注意:
使用反演定理时:
- 注意加括号保持运算顺序不变。原来该先计算的,反演之后也先计算
- 注意取反只针对单个变量比如:(A'+B'+C')',在取反时不操作外层的针对A'+B'+C'的反
3.对偶定理
加乘互换, 0 1 互换(其实是摩根定理和代入定理的组合形态)熟练使用对偶定理就可以少背一半公式
比如:
A(B+C)=AB+AC
A+(BC)=(A+B)(A+C) ……加乘、01互换
Y的对偶式用![]() 来表示
来表示
注意:
使用对偶定理时:
- 注意加括号保持运算顺序不变。原来该先计算的,对偶之后也先计算
逻辑运算公式
当然这里只介绍这些常用的啦
| 序号 | 公式 | 序号 | 公式 |
| 10 | 1‘=0;0’=1 | ||
| 1 | 0A=0 | 11 | 1+A=1 |
| 2 | 1A=A | 12 | 0+A=A |
| 3 | AA=A | 13 | A+A=A |
| 4 | AA'=0 | 14 | A+A'=1 |
| 5 | AB=BA | 15 | A+B=B+A |
| 6 | A(BC)=(AB)C | 16 | A+(B+C)=(A+B)+C |
| 7 | A(B+C)=AB+AC | 17 | A+BC=(A+B)(A+C) |
| 8 | (AB)'=A'+B' | 18 | (A+B)'=A'B' |
| 9 | (A')'=A |
逻辑函数的化简
逻辑函数可以表达为多种形式,两种标准形式是最小项之和 以及 最大项之积。后面一种不常用,所以这里只介绍最小项之和。「最小项之和也称作标准与或表达式」
最小项
标准表达:在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量都已原变量或反变量的形式在m中出现且仅出现一次,则这个乘积项m称为该函数的一个标准积项,通常称最小项。
直观理解:是一个“与”式,所有元素必须出来露面,还只能露面一次。
性质:
- 任意一个最小项,只有一组变量取值使其为1
- 任意两个不同最小项的乘积必为0
- 全部最小项的和必为1
- 具有相邻性的两个最小项可以合并
这里解释一下第一条:最小项是一个与式,也就是说所有条件都满足,这个式子才能为1。所有条件都满足,也就是最小项里面每个元素都有固定的取值,又因为最小项包含所有变量,因此也就对应了一组唯一的变量取值。举个例子:A'BC'D',如果是最小项,那么它仅仅当A=0;B=1;C=0;D=0时才能取1,任何一个数改变,它就取0了。
由第一条可以很方便的推出下面的内容。
公式化简法
除了手工多变量化简必须这样做以外,用途不大。简单介绍一下
基本思想:
- 把相同的提出来,凑出1,利用或运算消项
- 消去冗余项
「冗余项:一个变量的原变量与反变量分别与其他变量与,这两个被与的变量单独取与(或者再加上其他无关变量)就是冗余项。举个例子:A'B+AC+BC,A的原变量和反变量分别和B、C与,那么这两个被与的变量单独与,组成的BC就是冗余项。如果BC带了其他无关变量,那仍然是冗余项,比如A'B+AC+BCXYZ,那么BCXYZ就是冗余项」 - 消去与式的某个因子
单独的一个原变量,或上其反变量与无关变量的与式,那么这个反变量可以消去。举个例子:A+A'BC,A是单独的原变量,或上了反变量A'以及其他无关变量BC的与式,那么A'可以消去,原式=A+BC - 加项
利用1=A+A',将某个与式展开,比如BC可以展开成BC1=BC(A+A')=ABC+A'BC,再结合其他方法化简
或者增加冗余项,比如看到A'B+AC,自行增加冗余项BCD,再结合其他方法化简
卡诺图化简法
用几何方法解决代数问题 !大家应该还记得格雷码这个东东。把逻辑相邻转化为几何相邻。卡诺图也是一样的。
| 0 | 1 | |
| 0 | A'B' | A'B |
| 1 | AB' | AB |
| 00 | 01 | 11 | 10 | |
| 0 | A'B'C' | A'B'C | A'BC | A'BC' |
| 1 | AB'C' | ABC' | ABC | ABC' |
| 00 | 01 | 11 | 10 | |
| 00 | A'B'C'D' | A'B'C'D | A'B'CD | A'B'CD' |
| 01 | A'BC'D' | A'BC'D | A'BCD | A'BCD' |
| 11 | ABC'D' | ABC'D | ABCD | ABCD' |
| 10 | AB'C'D' | AB'C'D | AB'CD | AB'CD' |
首先回忆一下最小项这个说法。n变量的逻辑函数,最小项中每个变量出来露一次脸,每个变量有两种取值,那总共有2^n个最小项的可能。这些可能中,出现在最终的与式中,能够左右局势的写1,没有出现的写0。就画出了卡诺图。
无关项:
无关项分为约束项和任意项。
约束项是指由于物理限制而不可能出现的取值。比如汽车的状态,只可能是前进、后退、停止的一种,不可能既前进又后退还停止。
任意项是指由于人为原因故意忽略的取值。比如从90-99分都是A等,那么个位数的值我们就可以忽略了。
因为无关项的存在不会影响输出,所以可以自由决定它们取0还是取1,用来帮助我们化简。卡诺图化简法和带有无关项式子的化简在这里就一并解释了。
eg:Y=A'CD'+A'BC'D'+AB'C'D';约束条件:AB'CD'+AB'CD+ABC'D'+ABC'D+ABCD'+ABCD=0
首先把卡诺图画出来:
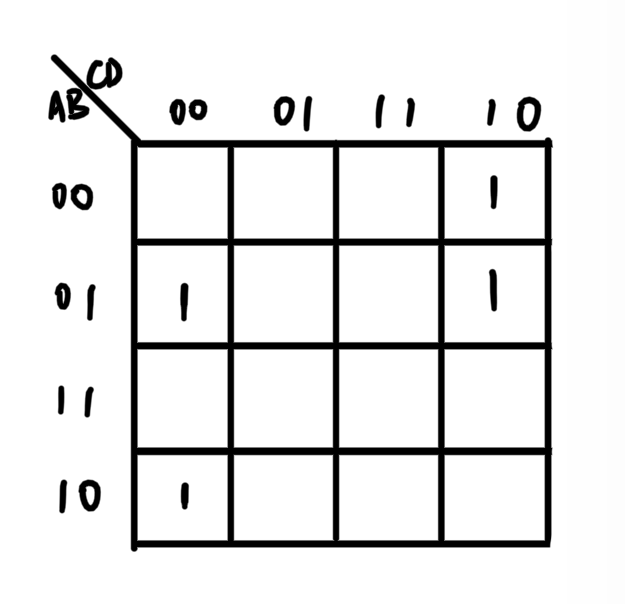
然后把无关项补进去,卡诺图里面使用×来表示无关项:
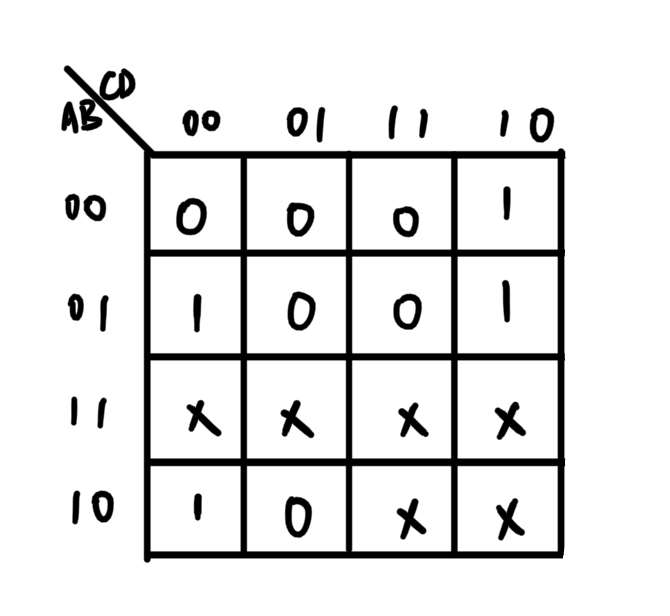
根据最小项的性质,相邻最小项可以合并,而卡诺图里面几何位置相邻就表示最小项相邻。所以应该找尽可能多的相邻1和×,用圈圈起来,进行化简:
- 每个圈只能圈2^n个1或者×
- 卡诺图四个顶点相邻、左右两遍相邻、上下两遍相邻
- 1和×可以重复被圈,但每个圈必须有至少一个1是只被圈过一次的
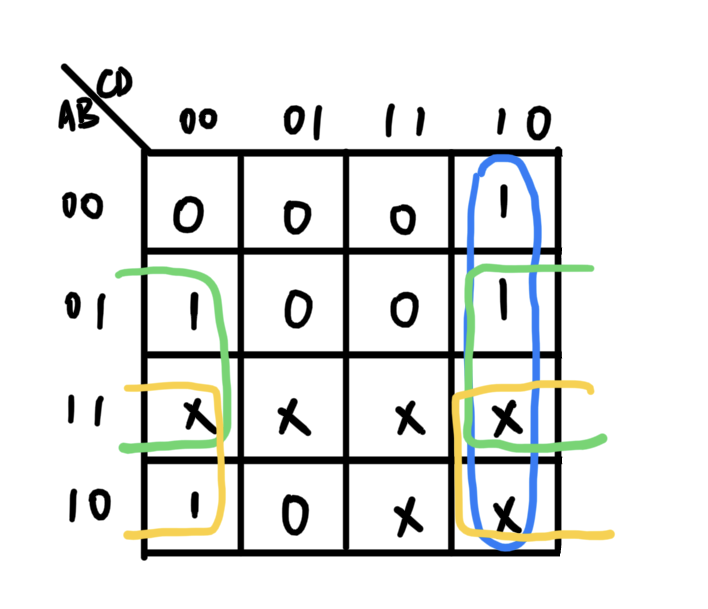
接下来可以根据圈来化简了:
蓝色:CD'
绿色:BD'
黄色:AD'
所以Y=AD'+BD'+CD'
最后
以上就是高高大树最近收集整理的关于「数字电子技术基础」3.逻辑代数基础逻辑代数基本逻辑运算常用组合逻辑运算逻辑代数基本定理逻辑运算公式逻辑函数的化简的全部内容,更多相关「数字电子技术基础」3.逻辑代数基础逻辑代数基本逻辑运算常用组合逻辑运算逻辑代数基本定理逻辑运算公式逻辑函数内容请搜索靠谱客的其他文章。








发表评论 取消回复