迁移学习综述(二)(学习笔记)
A Comprehensive Survey on Transfer Learning
1.引言
迁移学习的目标是利用来自相关领域(称为源领域)的知识,以提高学习性能或最小化目标领域中需要的标记示例的数量。知识转移并不总是对新任务产生积极的影响。如果领域之间几乎没有共同之处,知识转移可能不成功。例如,学习骑自行车并不能帮助我们更快地学习弹钢琴。以往的经验对学习新任务有负面影响的现象被称为负迁移。在迁移学习领域,如果目标学习者受到迁移知识的负面影响,这种现象也称为负迁移。负迁移是否会发生可能取决于几个因素,如源领域和目标领域之间的相关性,以及学习者发现跨领域知识的可迁移和有益部分的能力。
根据域之间的差异,转移学习可以进一步分为两类,即学习同质迁移和异质迁移。同质迁移学习方法被开发和提出来处理域具有相同特征空间的情况。在同质迁移学习中,一些研究假设领域只在边缘分布上存在差异。因此,他们通过修正样本选择偏差或协变量偏移。异质迁移学习是指领域具有不同特征空间情况下的知识迁移过程。除了分布适应外,异质性迁移学习还需要特征空间适应。
2.迁移学习与其他相关领域的联系和区别
2.1半监督学习(Semi-Supervised Learning):半监督学习是一种机器学习任务和方法,介于监督学习(完全标记的实例)和非监督学习(没有任何标记的实例)之间。通常,半监督方法利用大量的未标记实例和有限数量的标记实例来训练学习者。半监督学习放松了对标记实例的依赖,从而降低了昂贵的标记成本。注意,在半监督学习中,标记的和未标记的实例都来自同一个分布。相反,在迁移学习中,源域和目标域的数据分布通常是不同的。许多迁移学习方法吸收了半监督学习技术。半监督学习中的关键假设,即平滑性、聚类和流形假设,也被用于迁移学习。
2.2多视角学习(Multi-View Learning)/域自适应(Domain Adaptation):一个视角代表一个不同的特征集。关于多个视图的一个直观的例子是,一个视频对象可以从两个不同的视点描述,即,图像信号和音频信号。简单地说,多视图学习是从多个视图来描述一个对象,从而得到丰富的信息。通过适当地从各个角度考虑信息,学习者的表现可以得到提高。在多视角学习中,主要采用子空间学习、多核学习和联合训练等策略。在一些迁移学习方法中也采用了多视图技术。
- eg.Zhang等人提出了一种多视图迁移学习框架,该框架将多个视图之间的一致性强加在上。Yang和Gao在知识转移中整合了不同领域的多视图信息。Feuz和Cook的研究为活动学习引入了一种多视角迁移学习方法,该方法在异构传感器平台之间迁移活动知识
2.3多任务学习(Multi-Task Learning):多任务学习的思想是共同学习一组相关的任务。更具体地说,多任务学习通过利用任务之间的相互联系来强化每个任务,即同时考虑任务间的相关性和任务间的相关性的区别。这样,增强了每个任务的泛化。迁移学习与多任务学习的主要区别在于前者迁移相关领域所包含的知识,后者通过同时学习一些相关的任务进行知识的迁移。换句话说,多任务学习对每个任务的关注是均等的,而迁移学习对目标任务的关注多于对源任务的关注。迁移学习与多任务学习之间存在着一些共性和关联性。两者都旨在通过知识迁移来提高学习者的学习成绩。采用一些相似的模型构建策略,如特征变换和参数共享。值得注意的是,一些现有的研究同时利用了迁移学习和多任务学习技术。
- eg.Zhang等人将多任务和迁移学习技术用于生物图像分析。Liu等人提出了一种基于多任务学习和多源迁移学习的人类动作识别框架。
3.符号解释
参考《迁移学习(一)》
在上述基础上引入了多源域和多目标域,即:
{
(
D
S
I
,
T
S
i
)
∣
i
=
1
,
.
.
.
,
m
S
}
a
n
d
{
(
D
T
I
,
T
T
i
)
∣
i
=
1
,
.
.
.
,
m
T
}
{(D_{S_I},T_{S_i})|i=1,...,m^S} space space and space space{(D_{T_I},T_{T_i})|i=1,...,m^T}
{(DSI,TSi)∣i=1,...,mS} and {(DTI,TTi)∣i=1,...,mT}
迁移学习要学习的目标函数为:
f
T
j
(
j
=
1
,
.
.
.
,
m
T
)
f^{T_j}(j=1,...,m^T)
fTj(j=1,...,mT)
迁移学习领域常用的另一个术语是领域适应。领域适应是指通过调整一个或多个源领域来转移知识,从而提高目标学习者[4]的学习性能的过程。迁移学习往往依赖于领域适应过程,试图减少领域之间的差异。
4.迁移学习分类
详细配置参考《迁移学习(一)》
在上述基础上,总结分类如下:
(1)从问题角度
- 标签设置的分类【归纳式、直推式、无监督】
- 空间设置的分类 【同构(同质)迁移、异构(异质)迁移】
(2)从解决方法角度
- 基于实例迁移
- 基于特征迁移
- 基于参数迁移
- 基于关系迁移
这篇文章从数据和模型两个方面分类,基于数据的迁移方法包括了上述基于实例的迁移学习方法和基于特征的迁移学习方法。基于模型的涵盖了上述基于参数的方法。
5.基于数据(Data-based interpretation)
主要目的是通过实例加权和特征转换来减少源域和目标域实例之间的分配差异。
5.1实例加权
让我们首先考虑一个简单的场景,其中有大量标记的源域和有限数量的目标域实例可用,域只在边缘分布中不同(
P
S
(
X
)
≠
P
T
(
X
)
和
P
S
(
Y
∣
X
)
=
P
T
(
Y
∣
X
)
)
P^S(X) not= P^T(X)和P^S(Y|X) = P^T(Y|X))
PS(X)=PT(X)和PS(Y∣X)=PT(Y∣X))。
E
(
x
,
y
)
∼
P
T
[
L
(
x
,
y
;
f
)
]
=
E
(
x
,
y
)
∼
P
S
[
P
T
(
x
,
y
)
P
S
(
x
,
y
)
L
(
x
,
y
;
f
)
]
=
E
(
x
,
y
)
∼
P
S
[
P
T
(
x
)
P
S
(
X
)
L
(
x
,
y
;
f
)
]
E_{(x,y)}sim P^T[mathcal{L}(x,y;f)] =E_{(x,y)}sim P^S[cfrac{P^T(x,y)}{P^S(x,y)}mathcal{L}(x,y;f)] \=E(x,y)sim P^S[cfrac{P^T(x)}{P^S(X)}mathcal{L}(x,y;f)]
E(x,y)∼PT[L(x,y;f)]=E(x,y)∼PS[PS(x,y)PT(x,y)L(x,y;f)]=E(x,y)∼PS[PS(X)PT(x)L(x,y;f)]
m
i
n
f
1
n
S
∑
i
=
1
n
S
β
i
L
(
f
(
x
i
S
)
,
y
i
S
)
+
Ω
(
f
)
min_fcfrac{1}{n^S}sum_{i=1}^{n^S}beta _i mathcal{L}(f(x_i^S),y_i^S)+Omega(f)
minfnS1i=1∑nSβiL(f(xiS),yiS)+Ω(f)
β
i
(
i
=
1
,
.
.
.
,
n
S
)
beta_i(i=1,...,n^S)
βi(i=1,...,nS)就是权重参数。
- 5.1.1核均值匹配(KMM),通过在再生核希尔伯特空间(RKHS)中匹配源域和目标域实例之间的均值,解决了上述未知比率的估计问题。
a
r
g
m
i
n
β
I
∈
[
0
,
B
]
∥
1
n
S
∑
i
=
1
n
S
β
i
Φ
(
x
i
S
)
−
1
n
T
∑
j
=
1
n
T
β
j
Φ
(
x
j
T
)
∥
H
2
s
.
t
.
∣
1
n
S
∑
i
=
1
n
S
β
i
−
1
∣
≤
δ
argmin_{beta_Iin[0,B]}begin{Vmatrix}cfrac{1}{n^S}sum_{i=1}^{n^S}beta_iPhi(x_i^S)-cfrac{1}{n^T}sum_{j=1}^{n^T}beta_jPhi(x_j^T)end{Vmatrix}_{mathcal{H}}^2 \s.t. space space space |cfrac{1}{n^S}sum_{i=1}^{n^S}beta_i-1|leq delta
argminβI∈[0,B]∥∥∥∥nS1∑i=1nSβiΦ(xiS)−nT1∑j=1nTβjΦ(xjT)∥∥∥∥H2s.t. ∣nS1i=1∑nSβi−1∣≤δ
通过扩展和利用核技巧,将其转化为一个二次规划问题。这种估计分布比率的方法可以很容易地结合到许多现有的算法中。一旦获得权重βi,学习者就可以在加权源域实例上进行训练。
Sugiyama等人提出了一种称为Kullback-Leibler重要性估计程序(KLIEP)的方法。KLIEP依赖于Kullback-Leibler
(KL)散度的最小化,并合并了一个内置的模型选择过程。在研究权重估计的基础上,提出了一些基于实例的迁移学习框架或算法。
实例加权:为源域实例分配权值,以减少边际分布差异,类似于KMM
域加权:根据平滑性假设,为每个源域分配权值,以减少条件分布差异
-
5.1.2在TrAdaBoost中,将标记的源域实例和标记的目标域实例组合成一个整体,即一个训练集,训练弱分类器。对于源域和目标域实例,加权操作是不同的。在每次迭代中,计算一个临时变量δ,该变量测量标记的目标域实例的分类错误率。然后,根据δ和个体分类结果更新目标域实例的权值,根据设计的常数和个体分类结果更新源域实例的权值。为了更好地理解,重复给出第k次迭代(k
= 1,···,N)中更新权值的公式如下 β k , i S = β k − 1 , i S ( 1 + 2 l n n S N ) − ∣ f k ( x i S ) − y i S ∣ ( i = 1 , . . . , n S ) , β k , j T = β k − 1 , j T ( δ ˉ / ( 1 − δ ˉ ) ) − ∣ f k ( x j T ) − y j T ∣ ( j = 1 , . . . , n T ) , beta _{k,i}^S=beta _{k-1,i}^S(1+sqrt{2ln cfrac{n^S}{N}})-|f_k(x_i^S)-y_i^S|(i=1,...,n^S),\ beta _{k,j}^T=beta _{k-1,j}^T(bardelta/(1-bardelta))-|f_k(x_j^T)-y_j^T|(j=1,...,n^T), βk,iS=βk−1,iS(1+2lnNnS)−∣fk(xiS)−yiS∣(i=1,...,nS),βk,jT=βk−1,jT(δˉ/(1−δˉ))−∣fk(xjT)−yjT∣(j=1,...,nT),每次迭代形成一个新的弱分类器。最后的分类器是通过投票的方式将新产生的弱分类器的总数的一半。 -
5.1.3 Yao和Doretto[33]提出了一种多源TrAdaBoost(MsTrAdaBoost)算法,该算法在每次迭代中主要有以下两个步骤。
候选分类器构造:在每个源域和目标域成对的加权实例上分别训练一组候选弱分类器
实例权重:选择目标域实例上分类错误率最小的实例用于更新Ds和Dt中实例的权值。
以下实例类型用于构造目标分类器
- 标记目标域实例( Y T l Y_{T_l} YTl):分类器应该尽量减少它们的交叉熵损失,这实际上是一个标准的监督学习任务
- 未标记的目标域实例( Y T u Y_{T_u} YTu):这些实例的真实条件分布 P ( y ∣ x i T , U ) P(y|x^{T,U}_i) P(y∣xiT,U)是未知的,应该估计。一种可能的解决方案是在已标记的源域和目标域实例上训练辅助分类器,以帮助估计条件分布或为这些实例分配伪标签。
- 标记源域实例( Y S l Y_{S_l} YSl):作者定义 x i S , L x^{S,L}_i xiS,L的权值为两部分的乘积,即 α i α_i αi和 β i β_i βi。权重 β i β_i βi在理想情况下等于 P T ( x i ) / P S ( x i ) P^T(x_i)/P^S(x_i) PT(xi)/PS(xi),可以用KMM等非参数方法估计,也可以在最坏的情况下均匀地设置。权重 α i α_i αi用于过滤出与目标域差异较大的源域实例。
5.2特征转换
分类器使用来自相关领域的标记文本数据。在这个场景中,一种可行的解决方案是通过特征变换找到共同的潜在特征,并将其作为传递知识的桥梁。基于特征的方法将每个原始特征转化为新的特征表示,进行知识转移。构造新特征表示的目标包括最小化边缘和条件分布差异,保留数据的属性或潜在结构,以及找到特征之间的对应关系。特征变换的操作可以分为三种类型,即特征增强、特征缩减和特征对齐。
space space space
5.2.1分布差异度量
如何有效地度量域间的分布差异或相似度
最大均值差异(Maximum Mean difference, MMD)(KLD、JSD、BD、HSIC)
M
M
D
(
X
S
,
X
T
)
=
∥
1
n
S
∑
i
=
1
n
S
Φ
(
x
i
S
)
−
1
n
T
∑
j
=
1
n
T
Φ
(
x
j
T
)
∥
H
2
MMD(X^S,X^T)=begin{Vmatrix}cfrac{1}{n^S}sum_{i=1}^{n^S}Phi(x_i^S)-cfrac{1}{n^T}sum_{j=1}^{n^T}Phi(x_j^T)end{Vmatrix}_{mathcal{H}}^2
MMD(XS,XT)=∥∥∥∥nS1∑i=1nSΦ(xiS)−nT1∑j=1nTΦ(xjT)∥∥∥∥H2
PS:上面提到的KMM实际上通过最小化域之间的MMD距离来生成实例的权重
space space space
5.2.2特征增强
特征增强操作广泛应用于特征变换,尤其是基于对称特征的方法。具体来说,实现特征增强的方法有特征复制、特征叠加等。
-
Daume的工作提出了一种简单的域自适应方法,即特征增强法(FAM)。该方法通过简单的特征复制对原始特征进行变换。在单源迁移学习场景下,将特征空间扩大到原来的三倍。新的特征表示由一般特征、特定于源的特征和特定于目标的特征组成。注意,对于转换后的源域实例,它们特定于目标域的特征被设置为零。类似地,对于转换后的目标域实例,它们特定于源域的特征被设置为零。FAM的新特征表示如下
Φ S ( x i S ) = < x i S , x i S , 0 > , Φ T ( x j T ) = < x j T , 0 , x j T > Phi_S(x_i^S)=<x_i^S,x_i^S,0>,Phi_T(x_j^T)=<x_j^T,0,x_j^T> ΦS(xiS)=<xiS,xiS,0>,ΦT(xjT)=<xjT,0,xjT>
其中 Φ S Phi_S ΦS和 Φ T Phi_T ΦT表示源域和目标域到新特征空间的映射.最后的分类器将根据转换后的标记实例进行训练。值得一提的是,这种增广方法实际上是冗余的。换句话说,以其他方式(用更少的维度)扩展特性空间可能能够产生合格的性能。FAM算法的优点是其特征扩展形式优雅,具有多源场景下的泛化等优点。 -
FAM可能不能很好地处理异构迁移学习任务。这是因为当源域和目标域具有不同的特征表示形式时,直接复制特征和填充零向量的效果较差。为了解决这一问题,Li等人提出了一种称为异构特征增强(HFA)的方法。HFA的特征表示如下:
Φ S ( x i S ) = < W S x i S , x i S , 0 T > , Φ T ( x j T ) = < W T x j T , 0 S , x j T > Phi_S(x_i^S)=<W^Sx_i^S,x_i^S,0^T>,Phi_T(x_j^T)=<W^Tx_j^T,0^S,x_j^T> ΦS(xiS)=<WSxiS,xiS,0T>,ΦT(xjT)=<WTxjT,0S,xjT>HFA将原始特征映射到一个共同的特征空间,然后进行特征叠加操作。映射的特征、原始特征和零元素以特定的顺序堆叠以产生新的特征表示。
space space space 5.2.3特征映射
在传统的机器学习领域,有很多可行的基于映射的特征提取方法,如主成分分析(PCA)和核化PCA (KPCA)。然而,这些方法主要关注的是数据方差,而不是分布差异。迁移学习中也提出了很多基于特征映射的学习方法,让我们首先考虑一个简单的场景,其中域的条件分布没有什么区别。在这种情况下,可以使用以下简单的目标函数来查找用于特征提取的映射。
m i n Φ ( D I S T ( X S , X T ; Φ ) + λ Ω ( Φ ) ) / ( V A R ( X S ∪ X T ; Φ ) ) min_Phi(DIST(X^S,X^T;Phi)+lambda Omega(Phi))/(VAR(X^Scup X^T;Phi)) minΦ(DIST(XS,XT;Φ)+λΩ(Φ))/(VAR(XS∪XT;Φ))
Φ Phi Φ是低维特征映射函数, D I S T ( ⋅ ) DIST(cdot) DIST(⋅)表示分布之间的度量函数, Ω ( Φ ) Omega(Phi) Ω(Φ)是正则项, V A R ( ⋅ ) VAR(cdot) VAR(⋅)是实例的方差。
该目标函数的目标是找到一个映射函数 Φ Phi Φ,使域间的边缘分布差异最小化,同时使实例的方差尽可能大。分母对应的目标可以通过几种方式进行优化。一种可能的方法是用方差约束优化分子的目标。例如,可以将映射实例的分散矩阵强制为一个单位矩阵。另一种方法是先在高维特征空间中优化分子目标。然后,可以采用PCA或KPCA等降维算法来实现分母的目标。
space space space 找到 Φ ( ⋅ ) Phi (cdot) Φ(⋅)的显式公式也不是件容易的事。为了解决这一问题,一些方法采用线性映射技术或转向核技巧。一般来说,处理上述优化问题主要有三种思路: -
(映射学习+特征提取)一种可能的方法是通过解决核矩阵学习问题或变换矩阵寻找问题,首先找到一个目标满足的高维空间。然后,对高维特征进行压缩,形成低维特征表示。例如,一旦学习了核矩阵,就可以提取隐式高维特征的主成分,基于主成分分析构造新的特征表示。
-
(映射构造+映射学习)另一种方法是将原始特征映射到构造好的高维特征空间,然后学习一个低维映射来满足目标函数。例如,首先可以根据选定的核函数构造一个核矩阵。然后,学习变换矩阵,将高维特征投影到一个共同的潜在子空间中。
-
(直接低维映射学习)通常很难直接找到一个想要的低维映射。然而,如果假设映射满足某些条件,它可能是可解的。例如,如果低维映射被限制为线性映射,那么优化问题就很容易解决.
有些方法还试图匹配条件分布并保留数据的结构。为了实现这一点,上述简单的目标函数需要包含新的术语或/和约束。例如,下面的一般目标函数是一个可能的选择
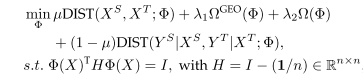
µ
µ
µ是平衡的边缘和条件分布差异的一个参数,
Ω
G
E
O
(
Φ
)
Omega ^{GEO}(Phi)
ΩGEO(Φ)是控制几何结构的正则项,
Φ
(
X
)
Phi(X)
Φ(X)矩阵的行是实例的源和目标域提取的新特性表示,
H
H
H是定心矩阵构造散射矩阵,约束是用于最大化方差。目标函数中的最后一项表示条件分布差异的度量。
PS:
D
I
S
T
(
X
S
,
X
T
;
Φ
)
DIST(X^S,X^T;Phi)
DIST(XS,XT;Φ)是源域和目标域实例差异度量
D
I
S
T
(
Y
S
∣
X
S
,
Y
T
∣
X
T
;
Φ
)
DIST(Y^S|X^S,Y^T|X^T;Phi)
DIST(YS∣XS,YT∣XT;Φ)是源域和目标域实例条件分布差异度量
值得一提的是目标域实例的标签信息通常是有限的,甚至是未知的。由于缺乏标签信息,很难估计分布差异。为了解决这个问题,一些方法诉诸伪标签策略,即,分配伪标签给未标记的目标域实例。实现这一点的一个简单方法是训练一个基分类器来分配伪标签。一旦伪标签信息被补充,条件分布差异就可以被测量。例如,可以对MMD进行修改和扩展,以度量条件分布差异。具体来说,对于每个标签,收集属于同一类的源域和目标域实例,并给出条件分布差异的估计表达式
∑
k
=
1
∣
y
∣
∥
1
n
k
S
∑
i
=
1
n
k
S
Φ
(
x
i
S
)
−
1
n
k
T
∑
j
=
1
n
k
T
Φ
(
x
j
T
)
∥
H
2
sum_{k=1}^{|y|}begin{Vmatrix}cfrac{1}{n_k^S}sum_{i=1}^{n_k^S}Phi(x_i^S)-cfrac{1}{n_k^T}sum_{j=1}^{n_k^T}Phi(x_j^T)end{Vmatrix}_{mathcal{H}}^2
k=1∑∣y∣∥∥∥∥nkS1∑i=1nkSΦ(xiS)−nkT1∑j=1nkTΦ(xjT)∥∥∥∥H2
- ( u = 1 a n d λ 1 = 0 u= 1 space and space λ_1 = 0 u=1 and λ1=0)Pan等人的工作提出了一种称为传递分量分析(TCA)的方法。TCA采用MMD来度量边际分布差,并强制散射矩阵作为约束。与MMDE学习核矩阵然后进一步采用PCA不同,TCA是一种统一的方法,只需要学习从经验核特征空间到低维特征空间的线性映射。这样避免了求解SDP问题,计算量相对较低。
- ( u = 0.5 a n d λ 1 = 0 u= 0.5 space and space λ_1 =0 u=0.5 and λ1=0)Long等人提出了联合分布适应(JDA)方法。试图找到一个转换矩阵,该矩阵将实例映射到一个低维空间,在这个空间中,边际和条件分布差异都被最小化。为了实现它,采用了MMDmetric和伪标签策略。通过特征分解求解轨迹优化问题,可以得到所需的变换矩阵。此外,很明显,估计的伪标签的准确性会影响JDA的性能。为了提高标注质量,采用了迭代的细化操作。具体来说,在每次迭代中执行JDA,然后使用提取的特征对实例进行分类器训练。接下来,根据训练的分类器更新伪标签。之后,使用更新的伪标签重复执行JDA。当收敛发生时迭代结束。
- ( u = ( 0 , 1 ) a n d λ 1 = 0 u= (0,1) space and space λ_1 =0 u=(0,1) and λ1=0)Wang等人的论文提出了均衡分布适应(BDA)方法,该方法是JDA的扩展。与JDA假设边际分布和条件分布在适应中同等重要不同,BDA试图平衡边际分布和条件分布的适应。BDA的操作类似于JDA。此外,作者还提出了加权BDA (WBDA)。在WBDA中,条件分布的差异通过MMD的加权版本来度量,以解决类别不平衡问题。
有些方法将特征转换为一个新的特征空间(通常是高维的),同时训练一个自适应分类器。为此,需要将特征的映射函数与分类器的决策函数相关联。一种可能的方法是定义以下决策函数
space space space
5.2.4特征聚类
特征聚类的目的是在原始特征的基础上找到更抽象的特征表示。虽然可以看作是一种特征提取的方法,但它不同于上述基于映射的提取方法。
space space space
5.2.5特征选择
特征选择是特征约简的另一种操作,用于提取枢轴特征。轴心特征是在不同领域以相同方式表现的特征。由于这些特征的稳定性,它们可以作为传递知识的桥梁。
space space space
5.2.7特征编码
深度学习领域常用的自动编码器可以用于特征编码。自动编码器由编码器和解码器组成。编码器试图产生输入的一个更抽象的表示,而解码器的目标是映射回该表示并最小化重构错误。自动编码器可以堆叠起来构建一个深度学习架构。一旦一个自动编码器完成了训练过程,另一个自动编码器可以堆叠在它的顶部。然后,使用上级自动编码器的编码输出作为其输入来训练新添加的自动编码器。
space space space
5.2.7特征对齐
特征增强和特征减少主要集中在特征空间中的显式特征上。相比之下,除了显式特征外,特征比对还侧重于一些隐式特征,如统计特征和光谱特征。因此,特征对齐在特征转换过程中可以发挥多种作用。可对齐的特征有多种,包括子空间特征、光谱特征和统计特征。以子空间特征对齐为例。典型的方法主要有以下步骤。
1.子空间生成:在这个步骤中,实例用于为源域和目标域生成各自的子空间。然后得到源域子空间和目标域子空间的标准正交基,分别用
M
S
M_S
MS和
M
T
M_T
MT表示。这些基用于学习子空间之间的转移。
2.子空间对齐:在第二步中,学习一个映射,将子空间的MS和MT基对齐。将实例的特征投影到对齐的子空间中,生成新的特征表示。
3.学习训练:最后,在转换的实例上训练目标学习者.
- Fernando等人提出了一种称为子空间对齐(SA)的方法[100]。在SA中,通过主成分分析(PCA)生成子空间;通过选择主要特征向量得到MS和MT的基值。然后,学习一个变换矩阵W来对齐已知b的子空间
W = a r g m i n W ∥ M S W − M T ∥ F 2 = M S T M T W=argmin_Wbegin{Vmatrix}M_SW-M_Tend{Vmatrix}_F^2=M_S^TM_T W=argminW∥∥MSW−MT∥∥F2=MSTMT
6.基于模型(Model-based interpretation)
迁移学习模型的主要目的是在目标域上做出准确的预测结果,例如分类或聚类结果。注意,迁移学习模型可能包含一些子模块,如分类器、提取器或编码器。这些子模块可能扮演不同的角色,如特征适配或伪标签生成。
6.1模型控制策略
模型的角度来看,一种自然的想法是直接在学习者的目标函数中添加模型级正则化器。这样,在训练过程中,可以将预获取的源模型中包含的知识转移到目标模型中。
Duan等人的论文提出了一种通用框架,称为域适应机器(DAM),该框架专为多源迁移学习而设计。DAM的目标是利用预先获得的基分类器在多个源域上分别训练,构建目标域的鲁棒分类器。
m
i
n
f
T
L
T
,
L
(
f
T
)
+
λ
1
Ω
D
(
f
T
)
+
λ
2
Ω
(
f
T
)
min_{f^T}mathcal{L^{T,L}}(f^T)+lambda_1Omega^D(f^T)+lambda_2Omega(f^T)
minfTLT,L(fT)+λ1ΩD(fT)+λ2Ω(fT)
L
T
,
L
(
f
T
)
mathcal{L^{T,L}}(f^T)
LT,L(fT)表示目标域实例的分类错误损失函数。
Ω
D
(
f
T
)
Omega^D(f^T)
ΩD(fT)表示不同的正则化器
Ω
(
f
T
)
Omega(f^T)
Ω(fT)用于控制最终决策函数
f
(
⋅
)
f(cdot)
f(⋅)的复杂性
一些迁移学习可以是上面的特例
- eg1(正则化器),Luo等人的研究提出了共识正则化框架(Consensus Regularizer framework,CRF)。CRF是为无标记目标域实例的多源迁移学习而设计的。该框架构造了对应于每个源域的
m
S
m^S
mS分类器,这些分类器需要在目标域上达成共识。每个源分类器的目标函数,用
f
k
S
f_k^S
fkS表示.
m i n f k S − ∑ i = 1 n S k l o g P ( y i S k ∣ x i S k ; f k S ) + λ 2 Ω ( f k S ) + λ 1 ∑ i = 1 n T , U ∑ y i ∈ Y S ( 1 m S ∑ k 0 = 1 m S P ( y i ∣ x i T , U ; f k 0 S ) ) min_{f_k^S}-sum_{i=1}^{n^{S_k}}logP(y_i^{S_k}|x_i^{S_k};f_k^S)+lambda_2Omega(f_k^S) \ +lambda_1sum_{i=1}^{n^{T,U}}sum_{y_iin mathcal{Y}}S(cfrac{1}{m^S}sum_{k_0=1}^{m^S}P(y_i|x_i^{T,U};f_{k_0}^S)) minfkS−i=1∑nSklogP(yiSk∣xiSk;fkS)+λ2Ω(fkS)+λ1i=1∑nT,Uyi∈Y∑S(mS1k0=1∑mSP(yi∣xiT,U;fk0S))
∑
i
=
1
n
S
k
l
o
g
P
(
y
i
S
k
∣
x
i
S
k
;
f
k
S
)
sum_{i=1}^{n^{S_k}}logP(y_i^{S_k}|x_i^{S_k};f_k^S)
∑i=1nSklogP(yiSk∣xiSk;fkS)是用于量化第
k
k
k个分类器在第
k
k
k个源域上的分类误差.
最后一项是交叉熵形式的共识正则化(
S
(
x
)
=
−
x
l
o
g
x
S(x)=-xlogx
S(x)=−xlogx).
一致性正则化不仅可以增强所有分类器的一致性,还可以减少目标域预测的不确定性。
- eg2(域相关的正则) Fast-DAM根据流形假设和基于图的正则化器设计了一个域相关的正则化器。目标函数为:
m i n f T ∑ j = 1 n T , L ( f T ( x j T , L ) − y j T , L ) 2 + λ 2 Ω ( f T ) + λ 1 ∑ k = 1 m S β k ∑ i = 1 n T , L ( f T ( x i T , U ) − f k S ( x i T , U ) ) 2 min_{f^T}sum_{j=1}^{n^{T,L}}(f^T(x_j^{T,L})-y_j^{T,L})^2+lambda_2Omega(f^T) \ +lambda_1sum_{k=1}^{m^S}beta_ksum_{i=1}^{n^{T,L}}(f^T(x_i^{T,U})-f_k^S(x_i^{T,U}))^2 minfTj=1∑nT,L(fT(xjT,L)−yjT,L)2+λ2Ω(fT)+λ1k=1∑mSβki=1∑nT,L(fT(xiT,U)−fkS(xiT,U))2
第三项是域相关的正则化。由领域依赖性驱动的源分类器。在[113]中,作者还在上述目标函数中引入了基于ε-不敏感损失函数的新项,使所得模型具有较高的计算效率。 - eg3(域依赖正则化+Universum正则化) Univer-DAM是Fast-DAM的扩展[。它的目标函数包含一个额外的正则化器,即优和正则化器。这个正则化器通常使用一个额外的数据集Universum,其中的实例既不属于正类也不属于负类。作者将源域实例作为目标域的优和,给出了Universum的目标函数:
m i n f T ∑ j = 1 n T , L ( f T ( x j T , L ) − y j T , L ) 2 + λ 2 ∑ j = 1 n S ( f T ( x j S ) ) 2 + λ 1 ∑ k = 1 m S β k ∑ i = 1 n T , L ( f T ( x i T , U ) − f k S ( x i T , U ) ) 2 + λ 3 Ω ( f T ) min_{f^T}sum_{j=1}^{n^{T,L}}(f^T(x_j^{T,L})-y_j^{T,L})^2+lambda_2sum_{j=1}^{n^S}(f^T(x_j^S))^2 \ +lambda_1sum_{k=1}^{m^S}beta_ksum_{i=1}^{n^{T,L}}(f^T(x_i^{T,U})-f_k^S(x_i^{T,U}))^2+lambda_3Omega(f^T) minfTj=1∑nT,L(fT(xjT,L)−yjT,L)2+λ2j=1∑nS(fT(xjS))2+λ1k=1∑mSβki=1∑nT,L(fT(xiT,U)−fkS(xiT,U))2+λ3Ω(fT)
6.2参数控制策略
参数控制策略的重点是模型的参数。例如,在对象分类的应用中,可以通过形状、颜色等对象属性将已知源类别的知识转化为目标类别。可以从源域学习属性先验,即每个属性对应的图像特征的概率分布参数,然后用于学习目标分类器。模型的参数实际上反映了模型学习到的知识。参数迁移又分为两种参数共享和参数约束。
6.2.1参数共享(Parameter Sharing)
一种直观的控制参数的方法是直接将源学习者的参数共享给目标学习者。参数共享在基于网络的方法中得到了广泛的应用。例如,如果我们有一个用于源任务的神经网络,我们可以冻结(或者说共享)它的大部分层,并只微调最后几层以产生一个目标网络。除了基于网络的参数共享,基于矩阵分解的参数共享也是可行的。
- 例如庄等人提出了一种文本分类方法,称为基于矩阵三因子分解的分类框架(MTrick)。作者观察到,在不同的领域,不同的词或短语有时表达相同或相似的内涵意义。因此,利用词汇背后的概念作为传递源域知识的桥梁,要比词汇本身更有效。其主要思想是将文档到单词矩阵分解为三个矩阵,即文档到集群、连接和集群到单词矩阵。具体来说,通过对源文档-字矩阵和目标文档-字矩阵分别进行矩阵三因子分解,构造了一个联合优化问题。
m i n Q , R , W ∥ X S − Q S R W S ∥ 2 − λ 1 ∥ X T − Q T R W T ∥ 2 + λ 2 ∥ Q S − Q ˉ S ∥ 2 N o r m a l i z a t i o n C o n t r a i n t s . min_{Q,R,W}begin{Vmatrix}X^S-Q^SRW^Send{Vmatrix}^2-lambda_1begin{Vmatrix}X^T-Q^TRW^Tend{Vmatrix}^2 \+lambda_2begin{Vmatrix}Q^S-bar Q^Send{Vmatrix}^2 \ space space space Normalization space space space Contraints. minQ,R,W∥∥XS−QSRWS∥∥2−λ1∥∥XT−QTRWT∥∥2+λ2∥∥QS−QˉS∥∥2 Normalization Contraints.
其中 X X X为文档的词矩阵, Q Q Q为文档簇矩阵, R R R为文档簇到文档的词的转换矩阵, W W W为簇到词矩阵, n d nd nd为文档数量, Q S Q^S QS为标签矩阵,是根据源域文档的类信息构造的。如果第 i i i个文档属于第 k k k类,则 Q S [ i , k ] = 1 Q^S [i,k] = 1 QS[i,k]=1。在上述目标函数中,矩阵 R R R是共享参数。第一项旨在对源文档到单词矩阵进行三因子分解,第二项分解目标文档到单词矩阵。最后一项包含源域标签信息。采用交替迭代法求解优化问题。得到 Q T Q^T QT的解后,第 k k k个目标域实例的类索引为 Q T Q^T QT第 k k k行中最大的类索引。 - 庄等进一步扩展了MTrick,提出了三层迁移学习(TriTL)。MTrick假设这些领域在它们的词簇背后有相似的概念。与此相反,TriTL假设这些领域的概念可以进一步分为三种类型,即独立于领域的概念、可转移的特定于领域的概念和不可转移的特定于领域的概念,这与HIDC类似。这种想法是由双重迁移学习(DTL)驱动的,在DTL中,概念被假定为由领域独立的概念和可迁移的领域特定的概念组成。
m i n Q , R , W ∑ k = 1 m S + m T ∥ X k − Q k [ R D I R T D R k N D ] [ W D I W k T D W k N D ] ∥ 2 min_{Q,R,W}sum_{k=1}^{m^S+m^T}begin{Vmatrix}X_k-Q_kbegin{bmatrix}R^{DIspace space R^{TD} space space R_k^{ND}}end{bmatrix} begin{bmatrix}W^{DI}\W_k^{TD}\W_k^{ND}end{bmatrix}end{Vmatrix}^2 minQ,R,Wk=1∑mS+mT∥∥∥∥∥∥Xk−Qk[RDI RTD RkND]⎣⎡WDIWkTDWkND⎦⎤∥∥∥∥∥∥2
6.2.2参数约束 (Parameter restriction)
与强制模型共享部分参数的参数共享策略不同,参数约束策略只要求源模型和目标模型的参数相似。以类别学习方法为例。分类学习问题是学习一个新的决策函数来预测一个新的类别(用第(k + 1)个类别表示),只需要有限的目标域实例和k个预先获得的二元决策函数。这些预先获得的决策函数的作用是预测一个实例属于k个类别中的哪一个。为了解决范畴学习问题,
- Tommasi等人提出了一种称为单模型知识转移(SMKL) 的方法。
- Tommasi等人利用所有预先获得的决策函数进一步扩展了SMKL.提出了一种称为多模型知识转移(MMKL) 的方法。(目标函数省略了,感兴趣可以自己查)
6.3模型集成策略
直接将数据或模型组合到单个域中可能不会成功,因为这些域的分布是不同的。模型集成是另一种常用的策略。该策略旨在结合多个弱分类器进行最终预测。前面提到的一些迁移学习方法已经采用了这一策略。例如TrAdaBoost和MsTrAdaBoost分别通过投票和加权对弱分类器进行整合。
- Gao等人的论文提出了另一种基于集成的框架,称为局部加权集成(LWE)。LWE注重不同学习者的整体学习过程;这些学习者可以在不同的源域上构建,也可以在单个源域上执行不同的学习算法来构建。不同于TaskTrAdaBoost每个学习者的学习全局权重,作者采用了局部权重策略,也就是说,将自适应权重分配给学习者基于局部流形结构的目标领域测试集。
- 上面提到的TaskTrAdaBoost和LWE方法主要关注的是整体过程。相比之下,一些研究更多地关注弱势学习者的构建。例如锚适配器的集成框架(ENCHOR)是Zhuang等人提出的加权集成框架。锚是一个特定的实例。与TrAdaBoost通过调整实例的权重来迭代地训练和产生一个新的学习者不同,enchant通过使用锚产生的实例的不同表示构造了一组弱学习者。这个想法是,一个特定的实例和一个锚点之间的相似性越高,该实例的特征相对于锚点保持不变的可能性就越大.
6.4深度学习技术
深度学习方法在机器学习领域尤为流行。许多研究者利用深度学习技术构建迁移学习模型。之前提到的SDA和mSLDA方法使用了深度学习技术。深度学习方法分为两类,即非对抗性(或者说传统的)和对抗性。
6.4.1传统深度学习(Traditional Deep Learning)
自动编码器经常用于深度学习领域。除了SDA和mSLDA,还有其他一些基于重构的迁移学习方法。
-
eg,Zhuang等人提出了一种基于深度自动编码器(Deep Autoencoders,
TLDA)的迁移学习方法。TLDA的源域和目标域分别采用两个自动编码器。这两个自动编码器共享相同的参数。编码器和解码器都有两层,具有激活功能。两种自动编码器的框图如下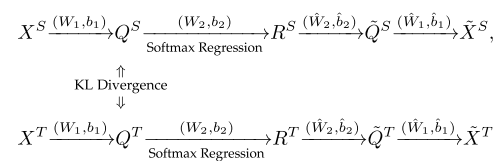
TLDA的目标有以下三点
1.重构误差最小化:解码器的输出应非常接近编码器的输入。也就是说, X S X^S XS和 X ˉ S bar X^S XˉS之间的距离以及 X T X^T XT和 X ˉ T bar X^T XˉT之间的距离应该最小化。
2.分布适应:最小化 Q S Q^S QS与 Q T Q^T QT间的分布差异。
3.回归误差最小化:编码器在标记的源域实例上的输出,即 R S R^S RS,应与对应的标签信息 Y S Y^S YS一致。
其中第一项表示重构误差, K L ( ⋅ ) KL(·) KL(⋅)表示 K L KL KL散度,第三项控制复杂度,最后一项表示回归误差。TLDA采用梯度下降法进行训练。最终的预测有两种不同的方法。第一种方法是直接使用编码器的输出进行预测。第二种方法是将自动编码器视为特征提取器,然后用编码器第一层输出产生的特征表示在标记的实例上训练目标分类器。 -
除了基于重构的域自适应外,基于差异的域自适应也是一个流行的方向。Long等人进行了多层自适应,并利用了多核技术,提出了一种称为深度自适应网络(DAN)的体系结构。
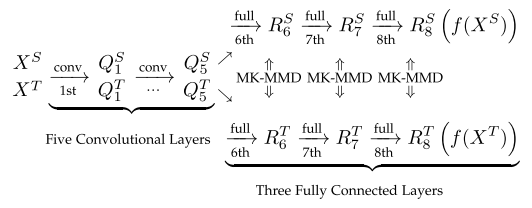
在上述网络中,首先通过5个卷积层,按通用化的方式提取特征。然后,提取的特征被输入到两个完全连接的网络中的一个。这两个网络都由三个完全连接的层组成,这些层专门用于源域和目标域。DAN有以下目标。
1.最小化分类错误:最小化已标记实例的分类错误。采用交叉熵损失函数对标记实例的预测误差进行度量。
2.分布适配:多层,包括表示层和输出层,可以以层的方式共同适配。作者转而使用MK-MMD,而不是使用单内核的MMD来测量分布差异。采用MK-MMD的线性时间无偏估计,避免了大量的内积运算
3.Kernel参数优化:对MK-MMD中多个Kernel的权重参数进行优化,使测试功率最大化。
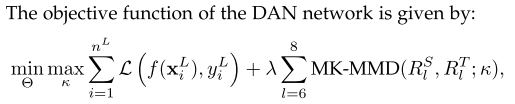
上述优化实际上是一个极大极小优化问题。目标函数相对于核函数κ的最大化,目标函数的目标是使测试幂最大化。在此步骤之后,源域和目标域之间的细微差别将被放大。这种思路类似于生成对抗网络(GAN)
6.4.2对抗深度学习(AdversarialDeep Learning)
对抗学习的思想可以整合到基于深度学习的迁移学习方法中。如上所述,在DAN框架中,网络
θ
θ
θ和核
κ
κ
κ都是极大极小对策,反映了对抗学习的思想。然而,DAN框架在对抗性匹配方面与基于gan的传统方法略有不同。在DAN框架中,
m
a
x
max
max博弈中需要优化的参数很少,这使得优化更容易达到均衡。在介绍对抗性迁移学习方法之前,让我们简要回顾一下最初的GAN框架及其相关工作。
- 原始的GAN灵感来自于两个游戏,由两个模型组成,生成器(Generator)和鉴别器(Discriminator)。为了迷惑鉴别器,使鉴别器产生错误的检测,产生伪造的真实数据.该鉴别器将真实数据和伪造数据混合输入,目的是检测数据的真伪。这两个模型实际上是一个极大极小博弈,目标函数如下
m i n G m i n D E x ∼ P t r u e [ l o g D ( X ) ] + E z ˉ ∼ P z ˉ [ l o g ( 1 − D ( G ( z ˉ ) ) ) ] min_{mathcal{G}}min_{mathcal{D}}Epsilon _{xsim P_{true}}begin{bmatrix}logmathcal{D}(X)end{bmatrix}+Epsilon _{bar zsim P_{bar z}}begin{bmatrix}log(1-mathcal{D}(mathcal{G}(bar z)))end{bmatrix} minGminDEx∼Ptrue[logD(X)]+Ezˉ∼Pzˉ[log(1−D(G(zˉ)))] 其中 z ˉ bar z zˉ表示噪音实例(从一定的噪声分布采样)作为输入的生成器生成的假样本。整个GAN可以通过反向传播算法进行训练。当两人博弈达到均衡时,生成器可以产生几乎看起来真实的实例。
在GAN的激励下,许多迁移学习方法建立在假设良好的特征表示几乎不包含关于实例原始领域的歧视性信息的基础上。
- eg,Ganin等人提出了一种深度架构,称为领域对抗神经网络(DANN),用于领域适应。DANN假设没有标记的目标域实例可以使用。它的体系结构由特征提取器、标签预测器和域分类器组成。对应的图表如下。
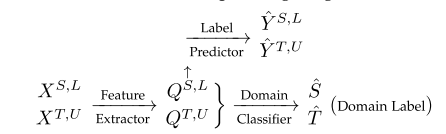
特征提取器的作用类似于生成器,目的是产生与领域无关的特征表示,以迷惑领域分类器。域分类器扮演着像鉴别器一样的角色,它试图检测提取的特征是来自源域还是目标域。标签预测器根据已标注源域实例的特征(即 Q S , L Q^{S,L} QS,L)进行训练,生成实例的标签预测。通过插入一个特殊的梯度反转层(GRL)来训练DANN。经过整个系统的训练后,特征提取器学习实例的深层特征,输出的 Y T , U Y^{T,U} YT,U为未标记目标域实例的预测标签.
些方法是为某些特殊场景设计的。以部分迁移学习为例。部分迁移学习方法是针对源域类比目标域类少的情况而设计的。在这种情况下,具有不同标签的源域实例可能具有不同的标签.
- Zhang等人的论文提出了一种局部域适应方法,称为重要性加权对抗网域适应(IWANDA)。IWANDA的建筑风格与DANN的不同。DANN采用一种共同的特征提取器,假设存在一个共同的特征空间,其中QS,L和QT,U具有相似的分布。然而,对于源域和目标域,IWANDA分别使用了两种特定领域的特征提取器。具体来说,IWANDA由两个特征提取器、两个域分类器和一个标签预测器组成。下面是IWANDA的图表
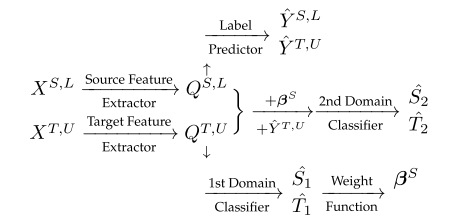
在训练之前,源特征提取器和标签预测器在有标记的源域实例上进行预先训练。这两个部分在训练过程中被冻结,这意味着只需要对目标特征提取器和领域分类器进行优化。在每次迭代中,通过以下步骤对上述网络进行优化
- 实例加权:为解决局部转移问题,根据第一个域分类器的输出为源域实例分配权重。第一个域分类器输入QS,L和QT,U,然后输出它们域的概率预测。如果源域实例很有可能属于目标域,那么该实例很有可能与目标域关联。因此,这个实例被赋予更大的权值,反之亦然。
- 预测制作:标签预测器输出实例的标签预测。第二个分类器预测实例属于哪个域。
- 参数更新:优化第一个分类器以最小化域分类错误。第二分类器与目标特征提取器进行最小最大博弈。这个分类器的目的是检测实例是否实例从目标域或加权实例从源域,并降低标签的不确定性预测ˆ欧美,U。目标特征提取器的目的是迷惑第二分类器。这些组件可以通过类似于GAN或插入GRL的方式进行优化
7.实验(Experiment)
在目标识别和文本分类两个主流研究领域,评价不同类别中一些有代表性的迁移学习模型的性能的实验.
D
a
t
a
s
e
t
:
O
f
f
i
c
e
31
、
R
e
u
t
e
r
s
−
21578
、
A
m
a
z
o
n
R
e
v
i
e
w
s
Dataset:Office31、Reuters-21578、Amazon Reviews
Dataset:Office31、Reuters−21578、AmazonReviews

在性能较好的算法中,
H
I
D
C
HIDC
HIDC和
M
T
r
i
c
k
MTrick
MTrick是基于特征约简(特征聚类),其他的是基于特征编码(
S
D
A
SDA
SDA)、特征对齐(
S
F
A
SFA
SFA)和特征选择(
S
C
L
SCL
SCL)。这些策略是目前基于特征的迁移学习的主流。
(没有细看,省略。。。。。。。。)
8.总结
在迁移学习领域,未来的研究方向有很多。首先,迁移学习技术可以进一步探索并应用于更广泛的应用领域。在更复杂的情况下,需要新的方法来解决知识转移问题。例如,在真实场景中,有时用户相关源域数据来自另一家公司。在这种情况下,如何在保护用户隐私的同时转移源域中所包含的知识是一个重要的问题。其次,如何衡量企业的跨领域可转移性,避免负迁移也是一个重要问题。虽然对负迁移已有一些研究,但负迁移还需要进一步的系统分析。第三,迁移学习的可解释性也需要进一步研究。最后,可以进一步开展理论研究,为迁移学习的有效性和适用性提供理论支持。迁移学习作为机器学习的一个热门和有发展前景的领域,与传统的机器学习相比,具有数据依赖性小、标签依赖性小等优点。希望我们的工作能够帮助读者更好地了解研究现状和研究思路。
PS:个人学习笔记,仅供参考!
最后
以上就是勤劳鸡最近收集整理的关于迁移学习(二)的全部内容,更多相关迁移学习(二)内容请搜索靠谱客的其他文章。








发表评论 取消回复