学习目标

• 掌握随机数的产生
• 了解概率密度函数等函数的使用
• 掌握统计图表的绘制方法
  

1.随机数的产生

随机数是专门的随机试验的结果。在统计学的不同技术中需要使用随机数，比如在从统计总体中抽取有代表性的样本的时候，或者在将实验动物分配到不同的试验组的过程中，或者在进行蒙特卡罗模拟法计算的时候等等。
产生随机数有多种不同的方法。这些方法被称为随机数发生器。随机数最重要的特性是：它所产生的后面的那个数与前面的那个数毫无关系。本节将重点讲解几种常见的随机数产生方法。

1.1二项分布随机数

在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n = 1时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。

在MATLAB中，可以使用binornd函数产生二项分布随机数，其使用方法如下：
R = binornd(N,P)：N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，且N、P、R的形式相同。
R = binornd(N,P,m)：m是一个1×2向量，它为指定随机数的个数。其中N、P分别代表返回值R中行与列的维数。
R = binornd(N,P,m,n)：m,n分别表示R的行数和列数。
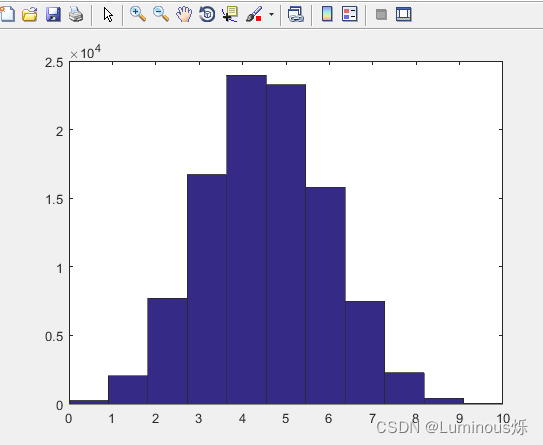
【例】某射击手进行射击比赛，假设每枪射击命中率为0.45，每论射击10次，共进行10万轮。用直方图表示这10万轮每轮命中成绩的可能情况。
在MATLAB中编写代码如下：

clear all
clc
x=binornd(10,0.45,100000,1);
hist(x,11);

运行程序，得到结果如下图所示。

1.2 泊松分布随机数

泊松分布是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩•德尼•泊松（Siméon-Denis Poisson）在1838年时发表。
泊松分布表达式为：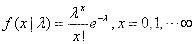
在MATLAB中，可以使用poisspdf函数获取泊松分布随机数，该函数调用格式如下：
y=poisspdf(x,lambda)：求取参数为Lambda的泊松分布的概率密度函数值。
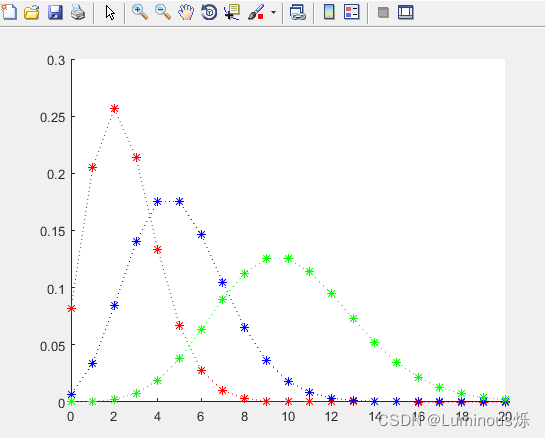
【例】取不同的Lambda值，使用poisspdf函数绘制泊松分布概率密度图像。
在MATLAB中编写以下代码：

clear all
clc
x=0:20;
y1=poisspdf(x,2.5);
y2=poisspdf(x,5);
y3=poisspdf(x,10);
hold on
plot(x,y1,':r*')
plot(x,y2,':b*')
plot(x,y3,':g*')
hold off

运行程序，得到不同Lambda值所对应的泊松分布概率密度图像如下图所示。

1.3 均匀分布随机数

MATLAB中提供均匀分布函数为unifrnd，其使用方法如下：
R=unifrnd(A,B)：生成被A和B指定上下端点[A,B]的连续均匀分布的随机数组R。如果A和B是数组，R(i,j)是生成的被A和B对应元素指定连续均匀分布的随机数。如果N或P是标量，则被扩展为和另一个输入有相同维数的数组。
R=unifrnd(A,B,m,n,…)或R=unifrnd(A,B,[m,n,…])：返回mn…数组。如果A和B是标量，R中所有元素是相同分布产生的随机数。如果A或B是数组，则必须是mn…数组。

1.4 正态分布随机数

MATLAB中提供正态分布函数为normrnd，其使用方法如下：
R = normrnd(mu,sigma)：返回均值为mu，标准差为sigma的正态分布的随机数据，R可以是向量或矩阵。
R = normrnd(mu,sigma,m,n,…)：m,n分别表示R的行数和列数
例如，如果需要得到mu为10、sigma为0.4的2行4列个正态随机数，可以在MATLAB命令行窗口输入以下代码：

R=normrnd(10,0.4,[2,4])

运行后得到结果为：

R =

   10.7351    9.6786   10.0997    9.9343
    9.5435    9.9385    9.5000    9.8592

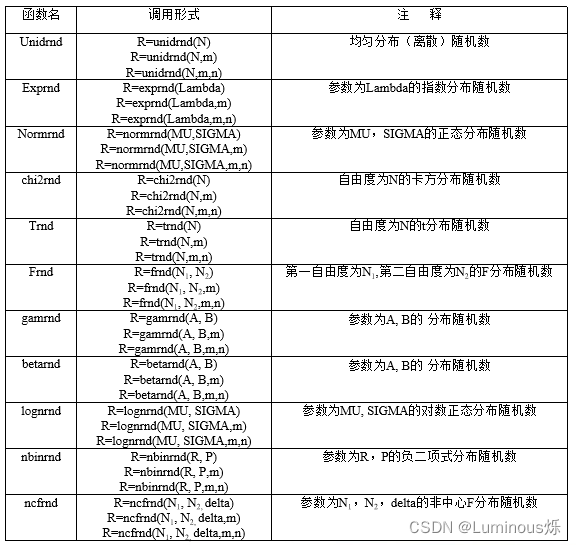
1.5 其他常见分布随机数

常见分布随机数的函数调用形式如下表所示。

2.概率密度函数

在数学中，连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。本节分别介绍常见分布的密度函数作图及使用函数计算概率密度函数值。

2.1 常见分布的密度函数作图

在MATLAB中，常见分布的密度函数有二项分布、卡方分布等多种。下面介绍几种常用的分布密度函数。
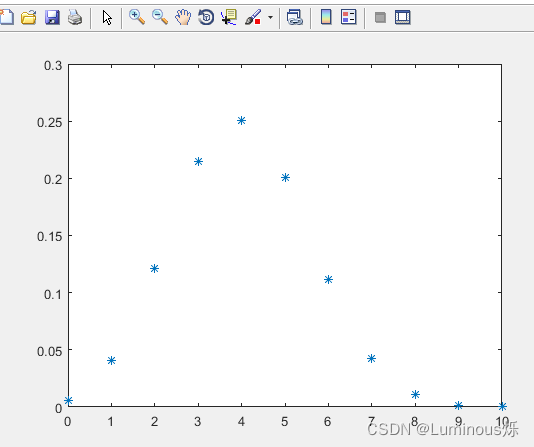
1.二项分布
在MATLAB中，绘制二项分布密度函数图像的代码如下所示：

clear all
clc
x = 0:10;
y = binopdf(x,10,0.4);
plot(x,y,'*')

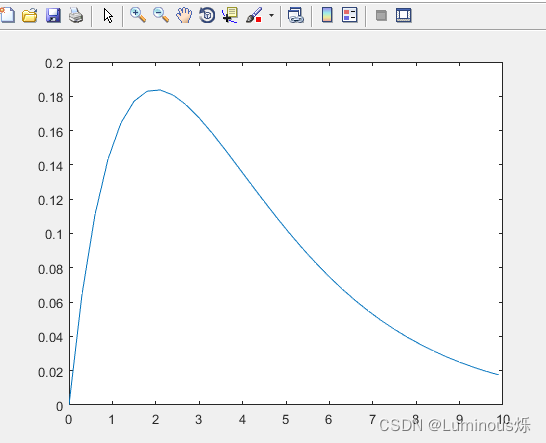
2.卡方分布
在MATLAB中，绘制卡方分布密度函数图像的代码如下所示：

clear all
clc
x = 0:0.3:10;
y = chi2pdf(x,4);
plot(x,y)

运行程序后，得到如下图像。

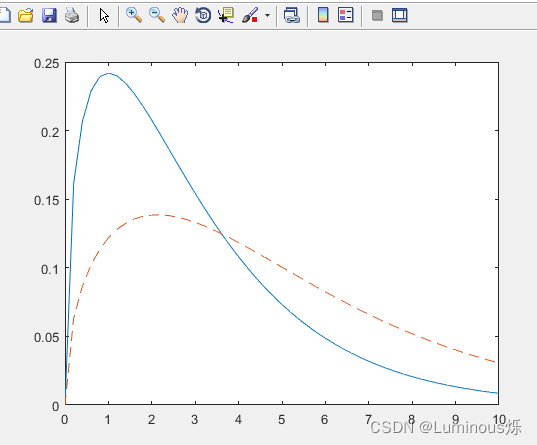
3.非中心卡方分布
在MATLAB中，绘制非中心卡方分布密度函数图像的代码如下所示：

clear all
clc
x = (0:0.2:10)';
p1 = ncx2pdf(x,3,2);
p = chi2pdf(x,3);
plot(x,p,'-',x,p1,'--')

运行程序后，得到如下图像。

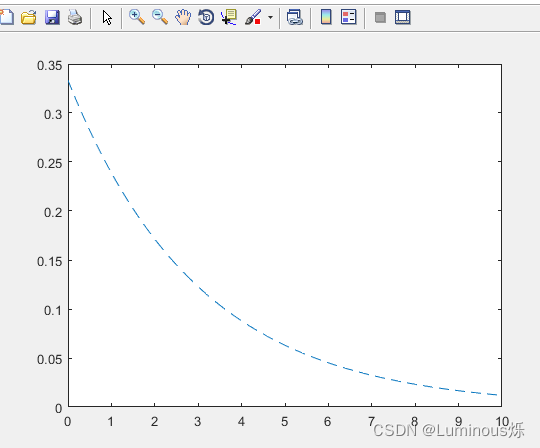
4.指数分布
在MATLAB中，绘制指数分布密度函数图像的代码如下所示：

clear all
clc
x = 0:0.2:10;
y = exppdf(x,3);
plot(x,y,'--')

运行程序后，得到如下图像。

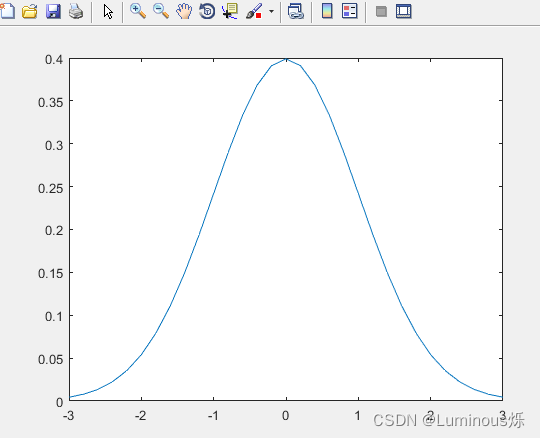
5.正态分布
在MATLAB中，绘制正态分布密度函数图像的代码如下所示：

clear all
clc
x=-3:0.2:3;
y=normpdf(x,0,1);
plot(x,y)

运行程序后，得到如下图像。

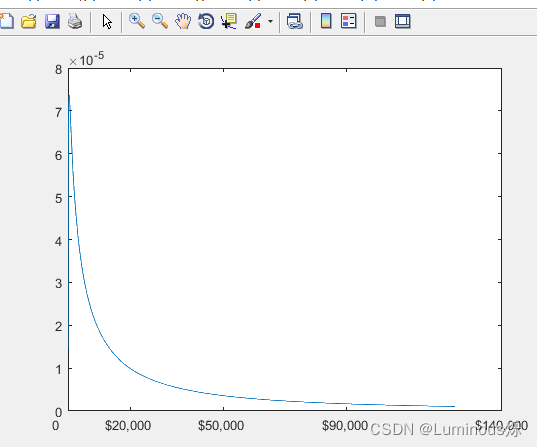
6.对数正态分布
在MATLAB中，绘制对数正态分布密度函数图像的代码如下所示：

clear all
clc
x = (10:100:125010)';
y = lognpdf(x,log(20000),2.0);
plot(x,y)
set(gca,'xtick',[0 20000 50000 90000 140000])
set(gca,'xticklabel',str2mat('0','$20,000','$50,000','$90,000','$140,000'))

运行程序后，得到如下图像。

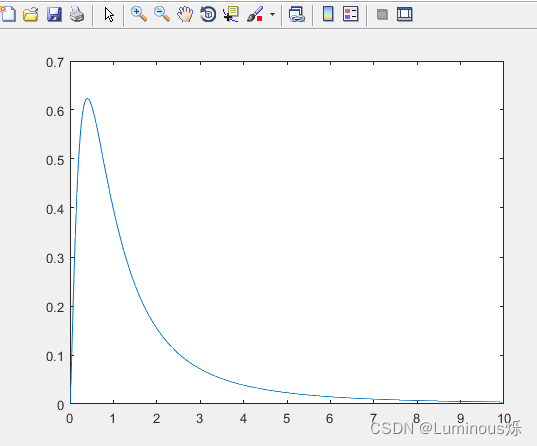
7.F分布
在MATLAB中，绘制F分布密度函数图像的代码如下所示：

clear all
clc
x = 0:0.02:10;
y = fpdf(x,5,4);
plot(x,y)

运行程序后，得到如下图像。

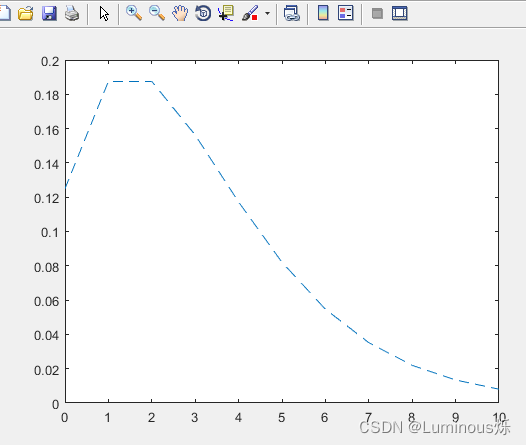
8.非中心F分布
在MATLAB中，绘制非中心F分布密度函数图像的代码如下所示：

clear all
clc
x = (0.02:0.2:10.02)';
p1 = ncfpdf(x,4,20,5);
p = fpdf(x,4,20);
plot(x,p,'-',x,p1,'--')

运行程序后，得到如下图像。

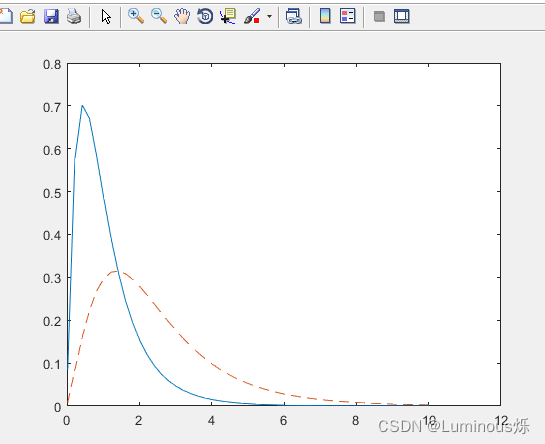
9.Γ分布
在MATLAB中，绘制Γ分布密度函数图像的代码如下所示：

clear all
clc
x = gaminv((0.005:0.01:0.995),100,10);
y = gampdf(x,100,10);
y1 = normpdf(x,1000,100);
plot(x,y,'--',x,y1,'-.')

运行程序后，得到如下图像。

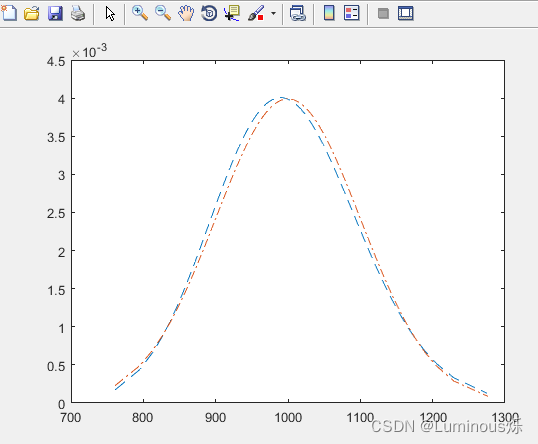
10.负二项分布
在MATLAB中，绘制负二项分布密度函数图像的代码如下所示：

clear all
clc
x = (0:10);
y = nbinpdf(x,3,0.5);
plot(x,y,'--')

运行程序后，得到如下图像。

2.2通用函数计算概率密度函数值

在MATLAB中，通用函数pdf可以计算概率密度函数值，其调用格式如下：
Y=pdf(name，K，A)
Y=pdf(name，K，A，B)
Y=pdf(name，K，A，B，C)：返回在X=K处、参数为A、B、C的概率密度值，对于不同的分布，参数个数是不同；name为分布函数名。

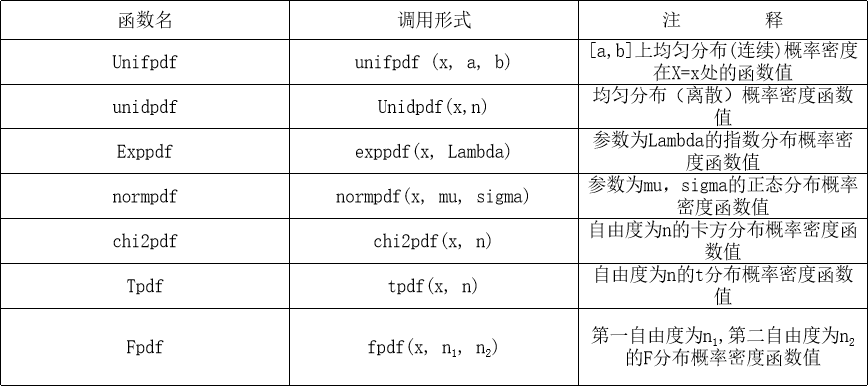
2.3专用函数计算概率密度函数值

专用函数计算概率密度函数列表如下表所示。

3.随机变量的数字特征

在解决实际问题过程中，往往并不需要全面了解随机变量的分布情况，而只需要知道它们的某些特征，这些特征通常称为随机变量的数字特征。常见的有数学期望、方差、相关系数和矩等。

3.1 平均值、中值

当X为向量时，算术平均值的数学含义为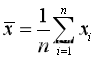，即样本均值。在MATLAB中，可以利用mean求X的算术平均值。函数mean的调用格式如下：
mean(X) %X为向量，返回X中各元素的平均值
mean(A) %A为矩阵，返回A中各列元素的平均值构成的向量
mean(A,dim) %在给出的维数内的平均值

3.2 数学期望

1.连续型随机变量的数学期望
设连续型随机变量x的概率密度为f(x)，若积分 绝对收敛，则称该积分的值为随机变量x的数学期望。
2.离散型随机变量的数学期望
设离散型随机变量x的分布律为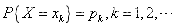：如果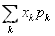绝对收敛，则称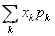的和为随机变量x的数学期望。

3.3 协方差及相关系数

在概率与统计中，随机变量X与Y的协方差Cov(X,Y))和相关系数ρ公式如下所示：
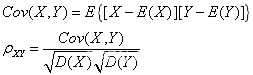设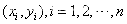是容量为n的二维样本，则样本的相关系数为：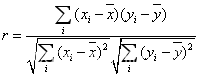
相关系数常常用来衡量两套变量之间的线性相关性，相关系数的绝对值越接近1，表示相关性越强，反之越弱。MATLAB中提供了cov函数计算样本协方差矩阵。

C=cov(X)：若X为单一矢量，则返回一个包含协方差的标量；若X的列为变量观测值的矩阵，则返回协方差矩阵。
C=cov(X,Y)=cov([X,Y])：X、Y为长度相等的列向量。
函数cov的算法如下：

[n,p]=size(X);
Y=X-ones(n,1)*mean(X);
C=Y'*Y./(n-1)

3.4 矩和协方差矩阵

MATLAB提供了moment函数计算样本的中心矩，其调用格式为：
m=moment(X,order)：返回X的order阶中心矩。对于矢量，moment(X,order)函数返回X数据的指定阶次中心矩。对于矩阵，moment(X,order)返回X数据的每一列的指定阶次中心矩。

3.5 数据比较

在MATLAB中，提供了多种函数进行数据比较，具体如下所示。
1.排序
在MATLAB中，提供排序功能的函数为sort，其调用格式如下：
Y=sort(X)：X为向量，返回X按由小到大排序后的向量。
Y=sort(A)：A为矩阵，返回A的各列按由小到大排序后的矩阵。
[Y,I]=sort(A)：Y为排序的结果，I中元素表示Y中对应元素在A中位置。
sort(A,dim)：在给定的维数dim内排序
2.按行方式排序
MATLAB提供按行方式排序的函数为sortrows，其调用格式如下所示：
Y=sortrows(A)：若A为矩阵，则返回矩阵Y，Y按A的第1列由小到大，以行方式排序后生成的矩阵。
Y=sortrows(A, col)：按指定列col由小到大进行排序
[Y,I]=sortrows(A, col)：Y为排序的结果，I表示Y中第col列元素在A中位置。
3.求最大值与最小值之差
MATLAB提供函数range求取参数的最大值与最小值之差，其调用格式如下：
Y=range(X)：X为向量，返回X中的最大值与最小值之差。
Y=range(A)：A为矩阵，返回A中各列元素的最大值与最小值之差。
函数range的使用示例如下。

A=[2 6 2;4 5 8;3 7 1]
Y=range(A)
Y=
  2   2   7

3.6 方差

MATLAB提供了包括求解样本方差和标准差的函数，分别是var和std，它们的调用格式如下所示：
D=var(X)：若X为向量，则返回向量的样本方差。
D=var(A)：A为矩阵，则D为A的列向量的样本方差构成的行向量。
D=var(X, 1)：返回向量（矩阵）X的简单方差（即置前因子为 的方差）
D=var(X, w)：返回向量（矩阵）X的以w为权重的方差
std(X)：返回向量（矩阵）X的样本标准差
std(X,1)：返回向量（矩阵）X的标准差（置前因子为 ）
std(X, 0)：与std (X)相同

3.7 常见分布的期望和方差

常见分布的期望和方差见下表所示

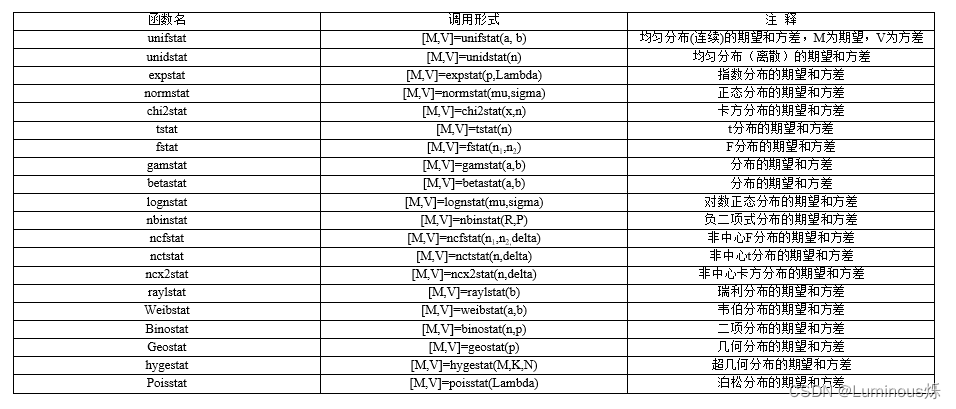
4.参数估计

参数估计的内容包括点估计和区间估计。MATLAB统计工具箱提供了很多参数估计相关的函数，例如计算待估参数及其置信区间、估计服从不同分布的函数的参数。

4.1常见分布的参数估计

MATLAB统计工具箱提供了多种具体函数的参数估计函数。
例如，利用normfit函数可以对正态分布总体进行参数估计。
[muhat,sigmahat,muci,sigmaci]=normfit(x)：对于给定的正态分布的数据x，返回参数 μ的估计值muhat、 σ的估计值sigmahat、μ 的95%置信区间muci、σ 的95%置信区间sigmaci。
[muhat,sigmahat,muci,sigmaci]=normfit(x, alpha)：进行参数估计并计算100(1-alpha)%置信区间。

4.2点估计

点估计是用单个数值作为参数的估计，目前使用较多的方法是最大似然法和矩法。
1.最大似然法
最大似然法是在待估参数的可能取值范围内，挑选使似然函数值最大的那个参数值为最大似然估计量。由于最大似然估计法得到的估计量通常不仅仅满足无偏性、有效性等基本条件，还能保证其为充分统计量，所以，在点估计和区间估计中，一般推荐使用最大似然法。
MATLAB用函数mle进行最大似然估计，其调用格式为：
phat=mle(‘dist’,data)：使用data矢量中的样本数据，返回dist 指定的分布的最大似然估计。
2.矩法
待估参数经常作为总体原点矩或原点矩的函数，此时可以用该总体样本的原点矩或样本原点矩的函数值作为待估参数的估计，这种方法称为矩法。
例如，样本均值总是总体均值的矩估计量，样本方差总是总体方差的矩估计量，样本标准差总是总体标准差的矩估计量。
MATLAB计算矩的函数为moment(X,order)。

4.3区间估计

求参数的区间估计，首先要求出该参数的点估计，然后构造一个含有该参数的随机变量，并根据一定的置信水平求该估计值的范围。
在MATLAB中用mle函数进行最大似然估计时，有如下几种调用格式：
[phat,pci]=mle(‘dist’,data)：返回最大似然估计和95%置信区间。
[phat,pci]=mle(‘dist’,data,alpha)：返回指定分布的最大似然估计值和100(1- alpha)%置信区间。
[phat,pci]= mle(‘dist’,data,alpha,p1)：该形式仅用于二项分布，其中p1为实验次数。

5.假设检验

在总体分布函数完全未知或部分未知时，为了推断总体的某些性质，需要提出关于总体的假设。对于提出的假设是否合理，需要进行检验。

5.1方差已知时的均值假设检验

在给定方差的条件下，可以使用ztest函数来检验单样本数据是否服从给定均值的正态分布。函数ztest的调用格式为：
h=ztest(x,m,sigma)：在0.05的显著性水平下进行z检验，以确定服从正态分布的样本的均值是否为m，其中sigma为标准差。
h=ztest(x,m, sigma ,alpha)：给出显著性水平的控制参数alpha。若alpha=0.01，则当结果h=1时，可以在0.01的显著性水平上拒绝零假设；若h=0，则不能在该水平上拒绝零假设。
[h,sig,ci,zval]=ztest(x,m,sigma,alpha,tail)：允许指定是进行单侧检验还是进行双侧检验。tail=0或‘both’时表示指定备择假设均值不等于m；tail=1或‘right’时表示指定备择假设均值大于m；tail=-1或‘left’时表示指定备择假设均值小于m；
sig为能够利用统计量z的观测值做出拒绝原假设的最小显著性水平，ci为均值真值的1-alpha置信区间，zval是统计量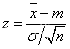的值。

5.2正态总体均值假设检验

在数理统计中，正态总计均值检测包括方差未知时单个正态总体均值的假设检验和两个正态总体均值的假设检验，其具体使用如下所示。
1.方差未知时单个正态总体均值的假设检验
t检验的特点是在均方差不知道的情况下，它是用小样本检验总体参数，可以检验样本平均数的显著性。
在MATLAB中可以使用ttest进行样本均值的t检验，其调用格式如下所示：
h=ttest(x,m)：在0.05的显著性水平下进行t检验，以确定在标准差未知的情况下取自正态分布的样本的均值是否为m。
h=ttest(x,m,alpha)：给定显著性水平的控制参数alpha。例如，当alpha=0.01时，如果h=1，则在0.01的显著性水平上拒绝零假设；若h=0，则不能在该水平上拒绝零假设。
[h,sig,ci]=ttest(x,m,alpha,tail)：允许指定是进行单侧检验还是进行双侧检验。tail=0或‘both’时表示指定备择假设均值不等于m；tail=1或‘right’时表示指定备择假设均值大于m；tail=-1或‘left’时表示指定备择假设均值小于m。sig为能够利用T的观测值做出拒绝原假设的最小显著性水平。ci为均值真值的1-alpha置信区间。

2.方差未知时两个正态总体均值差的检验
在比较两个独立正态总体的均值时，可以根据方差齐不齐的情况，应用不同的统计量进行检验。下面仅对方差齐的情况进行讲解。
用ttest2函数对两个样本的均值差异进行t检验，其调用格式为：
h=ttest2(x,y)：假设x和y为取自服从正态分布的两个样本。在它们标准差未知但相等时检验它们的均值是否相等。当h=1时，可以在0.05的水平下拒绝零假设；当h=0时，则不能在该水平下拒绝零假设。

5.3分布拟合假设检验

在统计分析中常常用到分布拟合检验方法，下面介绍两种比较简单的分布拟合检验方法，即q-q图法和峰度-偏度法。
1.q-q图
q-q图法就是用指定分布的分位数和变量数据分布的分位数之间的关系曲线来检验数据的分布。如两个样本来自同一分布，则图中数据点呈现直线关系，否则为曲线关系。该图中将样本数据用图形标记‘+’显示。在图中将每一个分布的四分之一和四分之三处进行连线，此连线线可以用来评价数据的线性特征。
MATLAB可以用qqplot函数生成样本q-q图
2.峰度-偏度检验
峰度-偏度检验又称为Jarque-Bera检验，该检验基于数据样本的偏度和峰度，评价给定数据是否服从未知均值和方差的正态分布的假设。对于正态分布数据，样本偏度接近于0，样本峰度接近于3。
Jarque-Bera检验可以确定样本偏度和峰度是否与它们的期望值相差较远。
在MATLAB中，使用jbtest函数进行Jarque-Bera检验，测试数据对正态分布的似合程度

6.方差分析

事件的发生总是与多个因素有关，而各个因素对事件发生的影响很可能不一样，且同一因素的不同水平对事件发生的影响也会有所不同。通过方差分析，便可以研究不同因素或相同因素的不同水平对事件发生的影响程度。
一般根据自变量个数的不同，将方差分析分为单因子方差分析和多因子方差分析。

6.1单因子方差分析

MATLAB中，anova1函数可以用于进行单因子方差分析

6.2 双因子方差分析

在MATLAB中，anova2函数可以用于进行单因子方差分析，其调用格式如下所示：
p=anova2(X,reps)：不同列中的数据代表一个因子A的变化。不同行中的数据代表另一因子B的变化。若在每一个行－列匹配点上有一个以上的观测值，则变量reps指示每一个单元中观测值的个数。
p=anova2(X,group,‘displayopt’)：当‘displayopt’参数设置为‘on’（默认设置）时，激活ANOVA表和箱形图的显示；‘displayopt’参数设置为‘off’时，不予显示。
[p,table]=anova2(…)：返回单元数组表中的ANOVA表（包含列标签和行标签）。
[p,table,stats]=anova2(…)：返回stats结构，用于进行列因子均值的多重比较检验。

7.计图表的绘制

因为图表的直观性，在概率和统计方法中，经常需要绘制图表。MATLAB提供了多种类型图表绘制函数。下面介绍几种常用的统计图表绘制函数。
1.正整数的频率表
绘制正整数频率表的函数是tabulate，其调用格式如下所示：
table = tabulate(X)：X为正整数构成的向量，返回3列。第1列中包含X的值，第2列为这些值的个数，第3列为这些值的频率。
2.经验累积分布函数图形
绘制经验累积分布函数图形的函数是cdfplot，其调用格式如下所示：
cdfplot(X)：作样本X（向量）的累积分布函数图形。
h = cdfplot(X)：h表示曲线的环柄。
[h,stats] = cdfplot(X) stats：表示样本的一些特征。
3.最小二乘拟合直线
绘制最小二乘拟合直线的函数是lsline，其调用格式如下所示：
h = lsline：h为直线的句柄。
4.绘制正态分布概率图形
绘制正态分布概率图形的函数是normplot，其调用格式如下所示：
normplot(X)：若X为向量，则显示正态分布概率图形，若X为矩阵，则显示每一列的正态分布概率图形。
h = normplot(X)：返回绘图直线的句柄。
5.绘制威布尔概率图形
绘制威布尔概率图形的函数是weibplot，其调用格式如下所示：
weibplot(X) %若X为向量，则显示威布尔(Weibull)概率图形，若X为矩阵，则显示每一列的威布尔概率图形。
h = weibplot(X) %返回绘图直线的柄。
6.样本数据的盒图
绘制样本数据的盒图的函数是boxplot
7.增加参考线
给当前图形加一条参考线的函数是refline
8.增加多项式曲线
在当前图形中加入一条多项式曲线的函数是refcurve
9.样本概率图形
绘制样本概率图形的函数是capaplot
10.附加有正态密度曲线的直方图
绘制附加有正态密度曲线的直方图的函数是histfit

总结

以上就是今天学习的内容，学过概率与统计的小伙伴可以试着熟悉以下方差、参数估计等所用到的这些函数，敲下代码哦！

最后

以上就是明亮摩托为你收集整理的【Matlab数理统计知识点合集】新手入门第十三天学习目标1.随机数的产生2.概率密度函数3.随机变量的数字特征4.参数估计5.假设检验6.方差分析7.计图表的绘制总结的全部内容，希望文章能够帮你解决【Matlab数理统计知识点合集】新手入门第十三天学习目标1.随机数的产生2.概率密度函数3.随机变量的数字特征4.参数估计5.假设检验6.方差分析7.计图表的绘制总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。