信道编码之分组码

通信原理相关系列目录请点击：通信原理相关目录

在讲分组码之前，强调一下，前面我们讲过了差错控制方式决定到底应该采用那种码，ARQ方式决定了用具有检错能力的码即可；FEC方式用可纠错的码组即可；而HEC则需要能够发现并纠正错误的码组。

因此，当最小码距d0 = 5时，如果按检错方式工作，则编码应具备检错能力，能检4个错误；

（由差错控制原理可知，最小码距为d0，则按检错方式工作，能检错d0-1个。）

如果按纠错方式工作，则编码应具备纠错能力，能纠正2个错误；

（同样由差错控制原理这篇博文可知，若按纠错方式工作，最小码距 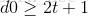，故能纠正2个错误。）

如果按混合方式工作，就能纠正一个错误，超出纠错能力还能检3个错误。（1+3+1=5）

（同样，由上篇博文差错控制原理可知，若采用混合方式工作，，其中d0为最小码距，e为检错个数，t为纠错个数，同时e>t，根据这两个关系，可知得知，e=3，t=1,也就是能纠错1位，检错3位。）

是不是就是说想要一种编码的纠错或检错的能力强，就要增加最小码距？那多添加点监督位就可以使最小码距增大了吧？

最小码距越大，监督位就越多。但码元的监督位增大，却不能说明码距也增大了，因此要提高编码的检错和纠错能力，不能仅靠简单地增加监督码元的位数，更重要的是要加大最小码距，也就是要增强码组之间的差异程度。

（这段话的意思就是要搞清楚一个逻辑，增加监督位与增大最小码距，是必要而非充分关系，也就是说增加监督位不一定能增大最小码距，但增大最小码距，就必须增大监督位。这就要涉及到如何增大监督位了，只有监督位取值合理，才能增加最小码距。如果我这段话看得更让人迷惑，那就忽略吧。）

如何添加监督位才能增大最小码距呢？（奇偶校验法）

最简单的办法是无论信息位有多少，都只添加一位监督位，这一位到底该添1还是0，主要是添加后它能否使码组中的1的数目，达到要求的偶数或者奇数而定，这种编码方法叫奇偶校验法。

要求1的数目为偶数，则称为偶校验；反之，为奇校验。

比如信息“云”，用01表示，加上一个监督位并且要编码后码组中的“1”为偶数，那么这个监督位就要为“1”，编码后得到的码组为“011”。如果接收端收到了001，那么它们模2加后就会得到1，这样就可以判断出接收的码组出现了错误，从而通知发送端重新发送这个码组。

所谓的模2加，就是逢2为0，但不进1；

不过这个例子中的最小码距为2，因此只能检测出一个错误。当接收到101时，虽然我们知道是发生了两个错误，但接收端通过计算，就会得出 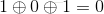 ,是判断不出发生了错误，因此接收端只能误判了。

同理，在奇校验中，就是无论信息位有多少，监督位只有一位，它使得码组中的1的数目为奇数，即满足如下条件：

.

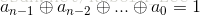奇偶校验只能检错不能纠错吗？

（这段纠错原理讲的不是太好，大致看一遍，明白个大致，最重要还是下面的具体例子）想要纠错，那就需要指出错误发生在哪个位置，而要指出错误发生在哪个位置，就需要多一些监督位来配合，在奇偶校验中，我们可以将监督码和信息码用一个关系式表达如下：

S为校正子，取值为0或1，在偶校验中，S为0正确，反之错误。

所以只有一位监督位时，只能指出码组是正确或者错误的，不能指出错误的位置。

如果增加一个监督位a1，就能建立两个关系式：

出现两个校正子，S1和S2，可能出现四种组合，表示四种不同的信息；

如果用其中一种组合表示有无错码，那么其余三种就可以用来指出一个错码的3种不同的位置；

同理，如果有r个监督关系式，则r个校正子可以指明一个错码的 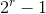个不同位置；

当校正子可以指明的错码位置数等于或大于码组长度n时，用公式表示如下：

就能够纠正码组中任何位置上的错码了。

举例说明，如何使用上述原理？

设计一个能够纠正1位错码的分组码（n,k），假设k = 4，根据上述不等式，即 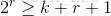，可知 监督位 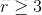，如果r=3，则码组长度n=k+r=7位，码组表示如下：

于是立即可得三个监督关系式：（？？？如何得到的，继续看下去）

根据偶校验的要求，三个校验子全为0：

所以根据移位计算，根据编码方程：（这位如何移的？）

可以解出监督位，这样给定信息位后，可据此直接计算监督位，便得到了编码结果。（解出监督位，这才是重点呀。好想法！）

（听了上述讲述，恐怕还是迷惑的，这三个监督关系式是怎么得到的呢？）

如果能确定监督关系式，也就能确定监督编码了，实际上，对于这几个监督关系式：

如果将模2加符号变成普通的加符号：

这就成了一个线性方程组了，因此这种编码也叫做线性分组码。

为了得到一个这样的线性方程组，人们会设法找到一个合适的生成矩阵基G，通过这个生成矩阵和给定的信息位，就可以产生整个编码码组：（在下面这个矩阵乘式中，生成矩阵基的维数为4*7，也就是k*n，即4行7列的一个矩阵！如何找到这个生成矩阵基呢？）

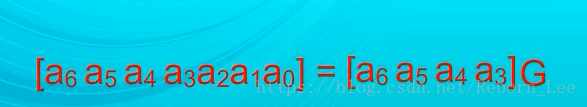
线性分组码都有那些应用呢？

循环码应用的比较多，循环码是重要的线性分组码，它除了具有线性分组码的一般线性外，还有循环特性，所以被称为循环码。

循环码的任何一个非全零码组位移动 i 次后，仍是一个许用码组；

下面是一个（7,3）循环码，任何一个码组移位1次，都会得到另外一个码组；比如第二码组向左移动1为就得到第三码组。

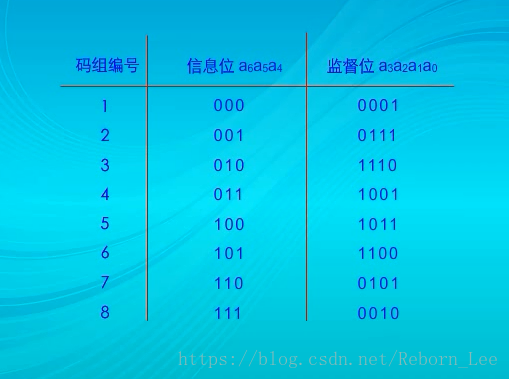
码距都为4，可以纠一个错，同时检2个错，循环码的优点在于其编码和译码手续比一般线性码简单，易于在设备上实现，且检错和纠错的能力都较强，而实际上用的较多的循环码当属循环冗余校验码了，简称CRC码，这种码不仅容易实现，而且检错能力很强，它所不能发现的错误的几率仅仅为0.0047%以下，所以在数据存储和数据通信领域，CRC码无处不在，著名的通信协议X.25采用的是CRC_CCITT，还有很多其他应用就不一一列举了。

如何生成CRC码呢？

关键是要找到一个生成多项式，有了生成多项式，就可以得到循环码的生成矩阵，而有了生成矩阵，根据前面所说的线性分组码的编码规则，就可以根据信息位得到相关的循环码组。

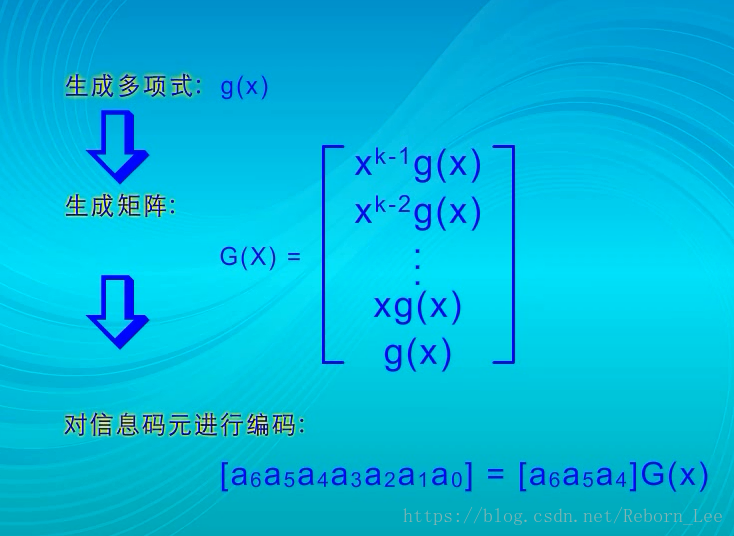
那生成多项式如何得到呢？

在CRC编码中，生成多项式是由CCITT制定的，如果我们要开发相关产品，可以捡现成的用，生成多项式如何求？

为了能用代数理论研究编码，通常会把码组中的各个码元当做一个多项式的系数，比如对于下面这个7位的码组，表示成码多项式就是如下：

这里的x的值是没有意义的，但它的幂表示了码元的位置，如x^6指的是第7个码元，所以码元系数对应为a6；因为是二进制编码，所以码元系数不是1就是0，对于如下码组，表示成码多项式如下：

分组编码到此结束。

（有了上述整个过程的层层讲解，以后要找个实例做做看！明确信息位长度，要纠错检错多少位，确定整个码组长度，然后根据上述过程求出监督位，这个编码就完成了。说着容易，做着也许会遇到困难，所以这里留个茬子，有时间了，一定要试试。）

最后

以上就是糟糕短靴为你收集整理的信道编码之分组码的全部内容，希望文章能够帮你解决信道编码之分组码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。