通信原理学习笔记4：信道编码、分组码、卷积码、现代信道编码（Turbo码、LDPC码、Polar码）

信道编码 / 前向纠错码FEC

思想是在数据中增加冗余信息，即校验码元 / 监督码元，从而检错、纠错

信道编码的优劣评判

• 首先，最基本的是要追求低差错率

实现纠错很简单，只要多添加冗余信息就好；但实际中，我们还需要考虑编/译码复杂度问题和开销问题：

• 编/译码复杂度低，可以节省算力资源、提高处理速度
• 保证纠错性能的同时，追求尽量小的开销（冗余比特）
  也就是说：好的信道编码，能够在一定的编码率$R=k/n$下（将$k$个信息位编码为总共$n$位），接近信道的容量的极限——香农极限

香农极限

根据香农第二定理，只要采用合适的信道编码，无差错传输的信息传输速率上限就是信道容量

• 也就是说，实现无差错传输，理论上的最大传输速率就是信道容量，我们称之为香农极限 / 香农容量
• 理论存在，那么实际中如何让信息速率逼近香农极限呢？需要采用足够长的随机编码

分组码有规则的代数结构，显然不是“随机”的，译码复杂度也限制了码长不能太长，因而远达不到香农极限；
后续的Turbo码、LDPC码、Polar码，才逐渐接近香农极限

信道编码举例

我们的思路是：

• 分组码：多个信息位成一组，对这一组比特追加校验位
  信息单独分块处理，其演进过程是重复码->汉明码->戈莱码->RM码->循环冗余校验CRC码
  缺点：每一组编码全部接收后才能译码；并且需要精确的帧同步才能正确译码
• 卷积码：对于当前输入的多个信息位，编码器的输出还与之前输入的信息位有关
  卷积码引入各个信息块之间的相关性（随着约束长度$N$增加，差错率指数下降）；并且编译码可以连续进行（无需等待整组信息）
• 现代信道编码：Turbo码、LDPC码、Polar码
  进一步逼近香农极限

LTE控制信道的信道编码就采用了$(3,1,7)$的卷积码；
3G、4G中广泛应用Turbo码（运用交织实现了“伪随机”，在高噪声环境下也性能优越）
5G的eMBB场景下，控制信道使用Polar码，数据信道使用LDPC码（更短时延要求更快的译码速度，而Turbo码的迭代译码被淘汰）

1. 分组码

$k$个信息位分为一组，增加$n-k$位冗余码元，总共得到$n$位数据，称为$(n,k)$分组码
$n-k$位冗余码元称为监督码元 / 校验码元，用于检错和纠错

分组码的矩阵表述：

生成矩阵

给出信息位的行向量${\mathbf{m}}_{1\times n}$，那么有一个生成矩阵${\mathbf{G}}_{k\times n}$可以生成分组码的码字行向量${\mathbf{C}}_{1\times n}$$${\mathbf{C}}_{1\times n}=\mathbf{m}\mathbf{G}=\left[\begin{array}{cccc}{\mathbf{c}}_1& {\mathbf{c}}_2& ...& {\mathbf{c}}_n\end{array}\right]$$
码字行向量$\mathbf{C}$的分量${\mathbf{c}}_{col}$（第col列）源于$\mathbf{m}$和$\mathbf{G}$的第col列相乘，也就是说，编码后每一位码字都是信息位$\mathbf{m}$的线性组合结果，如${\mathbf{c}}_4={\mathbf{m}}_2+{\mathbf{m}}_3$

校验矩阵

由上式改写可知，对于合法的码字$\mathbf{C}$，若校验信息长度$m=n-k$，那么各个码字之间一定满足$m$个方程的约束
例如，$(5,3)$分组码的合法码字满足$\{\begin{array}{c}{\mathbf{c}}_2+{\mathbf{c}}_3+{\mathbf{c}}_4=0\\ {\mathbf{c}}_1+{\mathbf{c}}_2+{\mathbf{c}}_3+{\mathbf{c}}_5=0\end{array}$（注意，以下一切加法为模2加），那么将其视为齐次线性方程组，${\mathbf{c}}_n$视为未知数，写为矩阵形式得到$\left[\begin{array}{ccccc}0& 1& 1& 1& 0\\ 1& 1& 1& 0& 1\end{array}\right]\left[\begin{array}{c}{\mathbf{c}}_1\\ {\mathbf{c}}_2\\ {\mathbf{c}}_3\\ {\mathbf{c}}_4\\ {\mathbf{c}}_5\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$

• 定义校验矩阵${\mathbf{H}}_{(n-k)\times n}=\left[\begin{array}{ccccc}0& 1& 1& 1& 0\\ 1& 1& 1& 0& 1\end{array}\right]$，可见所有合法码字${\mathbf{C}}^T$（列向量）构成了$\mathbf{H}$的零空间，即$$\mathbf{H}{\mathbf{C}}^T=0_{(n-k)\times 1}=\left[\begin{array}{c}0\\ ⋮\\ 0\end{array}\right]$$
• 实际上，校验矩阵$\mathbf{H}$和生成矩阵$\mathbf{G}$满足$\mathbf{H}{\mathbf{G}}^T=0_{(n-k)\times k}$（两者可以互相求出）

对于合法的码字行向量${\mathbf{C}}_{1\times n}^{\prime }$后，与校验矩阵$\mathbf{H}$做内积：若$\mathbf{H}({\mathbf{C}}^{\prime }{)}^T=0$，说明通过了校验，没有出错

标准/系统校验矩阵

根据线性方程组的理论，$\mathbf{H}$任意进行初等行变换，不改变校验位的约束关系（相当于消元）

由此，一般形式的$\mathbf{G}$和$\mathbf{H}$，对其做初等行变换，可以得到

• 系统生成矩阵${\mathbf{G}}_S={\left[\begin{array}{cc}{\mathbf{I}}_k& {\mathbf{Q}}_{k\times (n-k)}\end{array}\right]}_{k\times n}$
• 系统校验矩阵${\mathbf{H}}_S={\left[\begin{array}{cc}{\mathbf{Q}}_{(n-k)\times k}^T& {\mathbf{I}}_{(n-k)}\end{array}\right]}_{(n-k)\times n}$

这样做的好处是，所有信息位原样集中分布，所有校验位集中分布在码字的末尾

校验方法和伴随式

前面说过，合法的码字行向量${\mathbf{C}}_{1\times n}^{\prime }$与校验矩阵$\mathbf{H}$满足：$\mathbf{H}({\mathbf{C}}^{\prime }{)}^T=0$

实际中，接收码字行向量${\mathbf{r}}_{1\times n}$=原始码字${\mathbf{c}}_{1\times n}\oplus$错误图样${\mathbf{e}}_{1\times n}$

那么，对于接收码字行向量${\mathbf{r}}_{1\times n}$，校验方法就是计算${\mathbf{r}}_{1\times n}{\mathbf{H}}_{n\times (n-k)}^T={\mathbf{s}}_{1\times (n-k)}$，称${\mathbf{s}}_{1\times (n-k)}$为伴随式

• 如果伴随式${\mathbf{s}}_{1\times (n-k)}=0$，可能无差错 / 错误图样刚好为某个码字
• 如果伴随式${\mathbf{s}}_{1\times (n-k)}\ne 0$，必有差错

${\mathbf{s}}_{1\times (n-k)}\ne 0$时，纠错方法是：提前计算所有可能导致该结果的错误图样${\mathbf{e}}_{1\times n}$，并选择其中出错最少（1的个数最少）的作为最终的错误图样${\mathbf{e}}_{1\times n}$（上面说过，伴随式数量<=所有可能的错误情况，只能挑选最有可能的错误来纠正；若取=号则称为完备码）

重复码

三重复码：$0\to 000,1\to 111$，检2位错，纠1位错
问题是传输效率只有1/3，并且错2位就会导致译码出错

奇偶校验码

仅增加1位校验码元，保证分组码的码字中1的个数为偶数

• 检测奇数个错，不能纠错

汉明码

$(7,4)$汉明码，3位监督码元分别对信息码元中的某几位进行奇偶校验，多组奇偶校验共同形成了类似“方程组”的约束，从而能够纠错

• 检2位错，纠1位错

如图，$a_2$、$a_1$、$a_0$分别对某几个信息位做奇偶检验

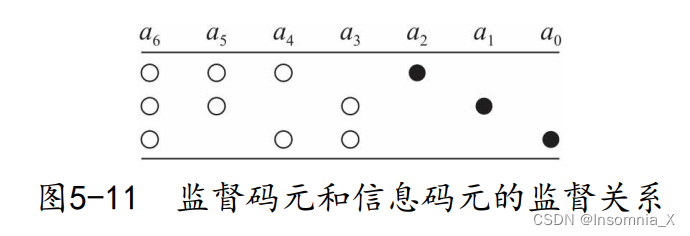
$$\{\begin{array}{c}{\mathrm{a}}_6\oplus {\mathrm{a}}_5\oplus {\mathrm{a}}_4\oplus {\mathrm{a}}_2=0\\ {\mathrm{a}}_6\oplus {\mathrm{a}}_5\oplus {\mathrm{a}}_3\oplus {\mathrm{a}}_1=0\\ {\mathrm{a}}_6\oplus {\mathrm{a}}_4\oplus {\mathrm{a}}_3\oplus {\mathrm{a}}_0=0\end{array}$$

接收端检错方法：分别对三组奇偶校验码进行验证：$$\{\begin{array}{c}{s}_2=a_6\oplus a_5\oplus a_4\oplus a_2\\ s_1=a_6\oplus a_5\oplus a_3\oplus a_1\\ s_0=a_6\oplus a_4\oplus a_3\oplus a_0\end{array}$$
若没有错误，则$s_2{s}_1{s}_0=000$；若$a_0$错误，则$s_2{s}_1{s}_0=001$；若$a_1$错误，则$s_2{s}_1{s}_0=010$…由此类推，仅一位出错时，7种可能的错误刚好对应了$s_2{s}_1{s}_0$的7种可能组合，进而可以相应纠错

2. 卷积码

之前的编码器：每次输入k 个信息码元，输出n个码元，编码器的输出只与本次输入的一组信息码元有关
卷积码：编码器的输出不仅与本次输入的一组信息码元有关，还与之前输入的$K$组信息码元有关

$(n,k,N)$卷积码，又时也记为$(n,k,m)$卷积码
对于每次输入的$k$个信息位，编码器输出$n$个码元

• 本次的输出涉及到当前及之前输入的总共$N$组信息（称约束长度/编码存储长度为$N$）；
  随着约束长度$N$增加，差错率指数下降
• 或者说本次输出与之前的$m=(N-1)$段信息有关；

也就是说，当前的编码器输出，被总共$k\cdot N$个输入信息位共同决定，编码器需要记忆之前的$k\cdot (N-1)$个信息位；
卷积码的编码输出结果中，共计有$n\cdot N$位码元是有关联的;

一般$k=1$，也就是说1个比特就是一组，即：每次对1bit编码，输出n bit，结果与当前以及前面的总共N bit有关

$(n,1,N)$卷积码，涉及到之前输入的$N-1$个信息位，因此需要$m=N-1$级移位寄存器实现
关系：$$寄存器级数/记忆长度m=约束长度N-1$$

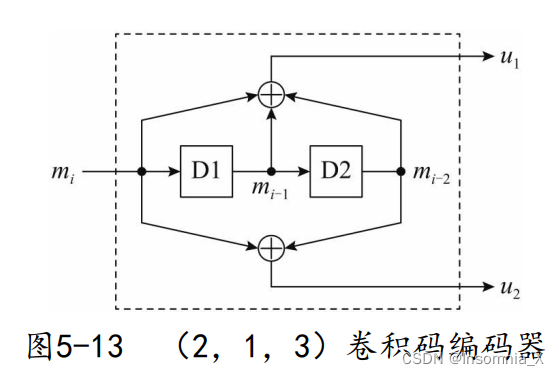
例如，一个$(2,1,3)$卷积码编码器，需要$m=N-1=2$级移位寄存器，原理如下：

编码器输出$u_1$涉及两个前面的输入：$u_1=m_i\oplus m_{i-1}\oplus m_{i-2}$
编码器输出$u_2$涉及一个前面的输入：$u_1=m_i\oplus m_{i-2}$

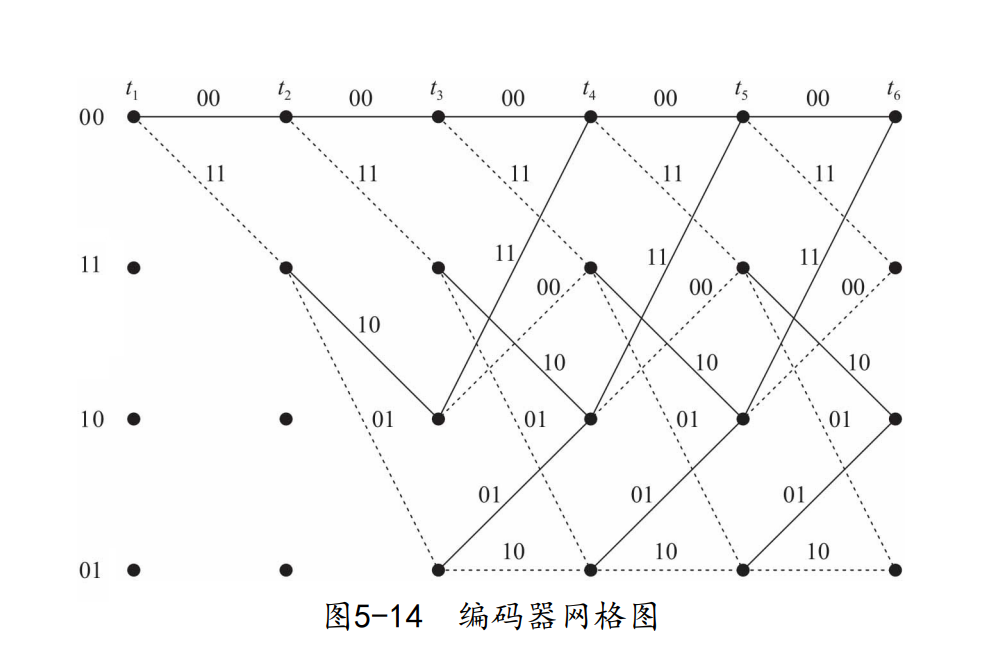
由于只有两级寄存器，寄存器中的数据只可能有四个状态：$00、01、10、11$，故编码器类似一个“状态机”，并且状态的转移取决于当前的输入，不能随意跳转，合法的“状态转移”表示为网格图如下：

图中从上到下的四个黑点代表寄存器四个状态；
实线代表输入0，虚线代表输入1；
实线和虚线旁的两位数字代表编码器的输出

例如，输入$100$，编码器输出$111011$

卷积码的Viterbi译码原理

认为发出的所有码字等概出现，因此可以采用最大似然译码ML，收到码字$Y$，将其译为码字$X$，则译码结果$X$应该使得$P(Y|X)$最大化；
理论上，最大似然译码ML应该遍历所有可能的编码器输出$X$，复杂度极高
但是我们在计算各个$X$对应的$P(Y|X)$时发现，从$X$到$Y$汉明距离最小时（即传输时错误的码元越少），$P(Y|X)$越大

可见，最大似然译码ML可以转化为：寻找与接收码字$Y$汉明距离最小（误码数最少）的码字$X$，这就是维特比译码，它大大减小了ML译码的计算量

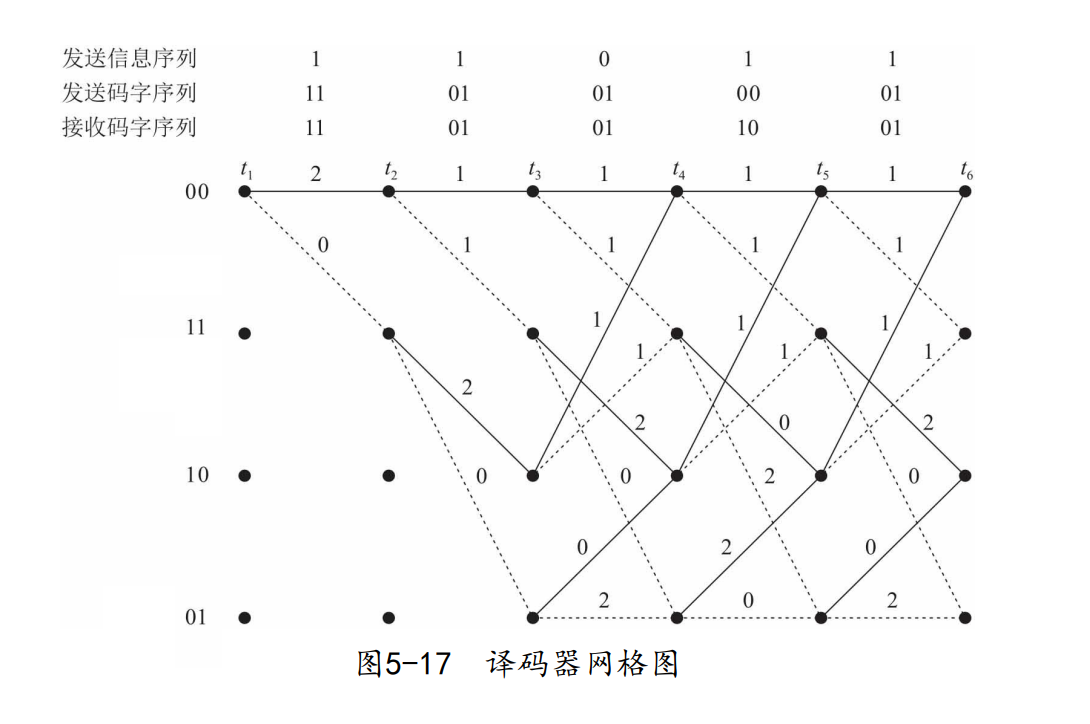
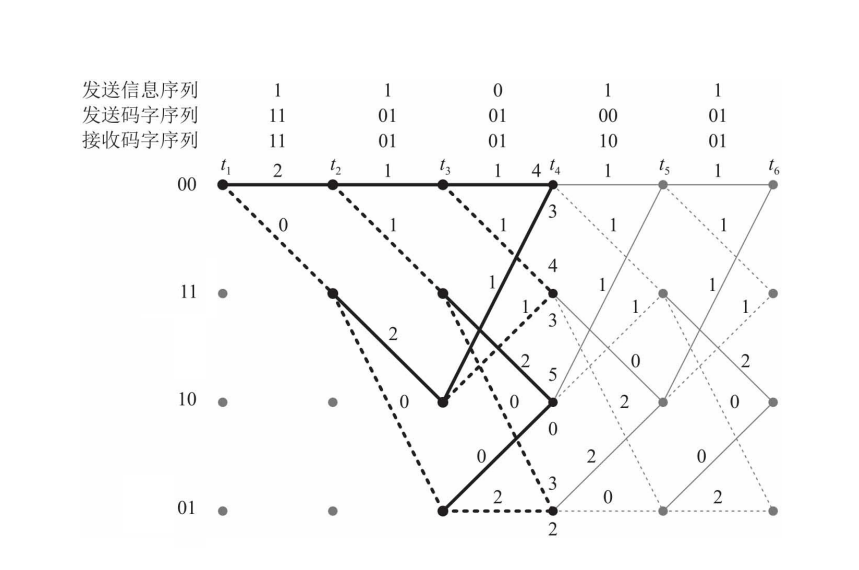
维特比译码仍使用网格图，目标是寻找一条最优路径，即与接收码字序列的汉明距离最小的路径

如图，首先写出接收码字序列$110101\underline{1}001$（有一位错误），实线和虚线代表译码输出结果为0 / 1，四个点对应卷积码编码的2位输出，实线和虚线旁的数字是每条支路与接收码字序列的汉明距离

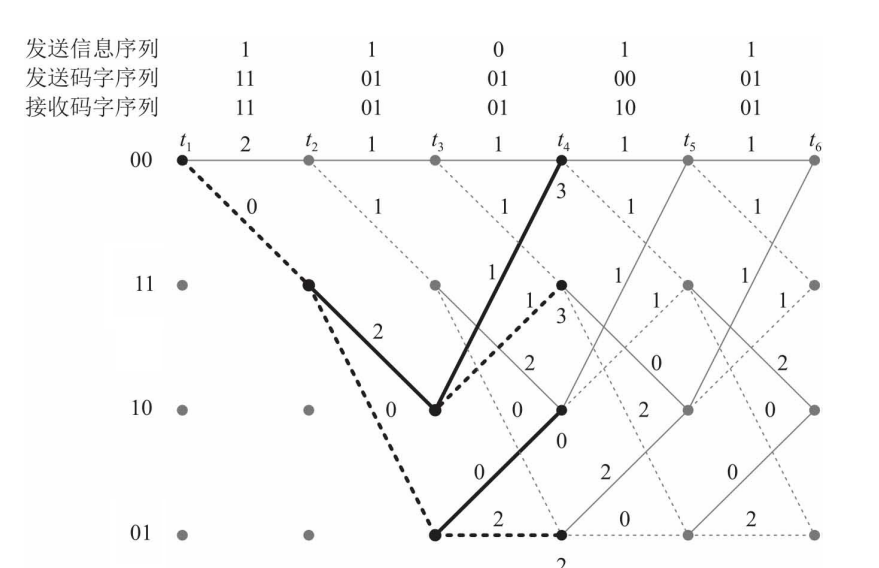
每步译码时，考虑所有可能的支路，并在节点处记录各个路径与接收码字的汉明距离（各段旁标注的汉明距离的累加）

当每个节点处存在2条可能路径时，舍弃汉明距离更大的那一条

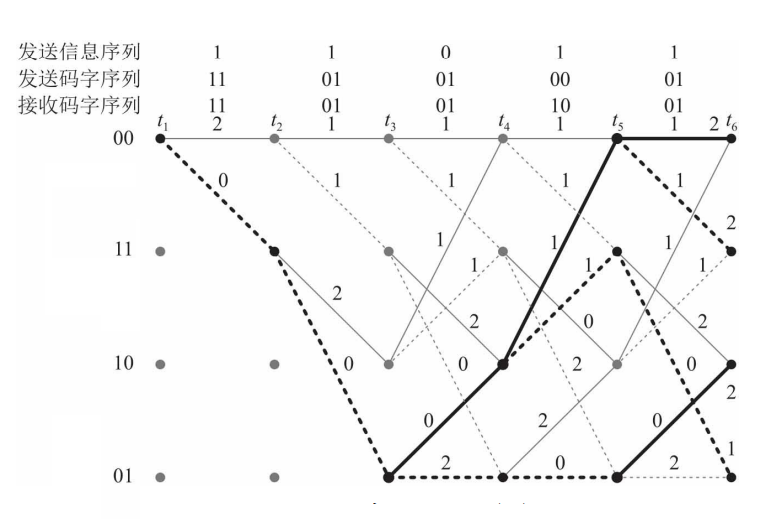
不断重复，直到最后一步，整个网格图种只剩下4条可能的路径

我们选取汉明距离最小的那条路径，则译码结果为$11011$

3. 现代信道编码

Turbo码

上面说，要使信道编码逼近香农极限（无差错传输，且信息速率接近信道容量），需要采用足够长的随机编码；
一方面要求随机，传统信道编码有规则的代数结构，不是随机的；
另一方面要求足够长，然而传统信道编码的码长不会太长，否则译码复杂度高

传统编码始终距离香农容量有2~3dB；
直到Turbo码巧妙运用交织，实现了“伪随机”，从而接近香农极限

Turbo编码器：并行放置两个卷积码编码器（称为分量编码器），由一个伪随机交织器连接；
最终，完整输出即“系统比特+第一校验比特+第二校验比特”
也就是说，将两个简单分量码通过交织器并行级联，从而构造了具有伪随机特性的长码；

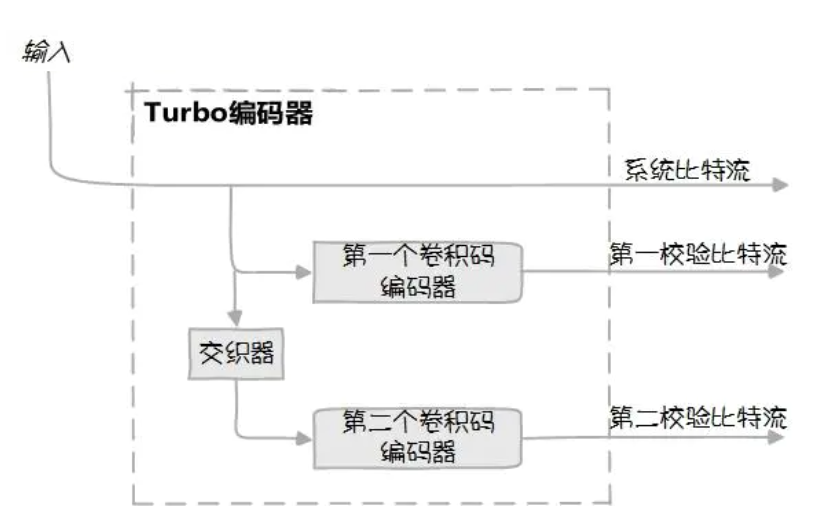
Turbo码增益就来自于这个交织器

Turbo伪随机译码器：串行放置的两个卷积码译码器（称为分量译码器），每个分量译码器的输出经过处理又作为另一译码器的输入，循环的进行迭代译码
在这个过程中分量译码器之间传递去掉正反馈的外信息（外信息就类似于除去单个译码器自身判断之外，另一译码器提供的信息），最终两个校验比特流共同贡献了译码的结果。
整个译码过程类似涡轮工作，故称Turbo码

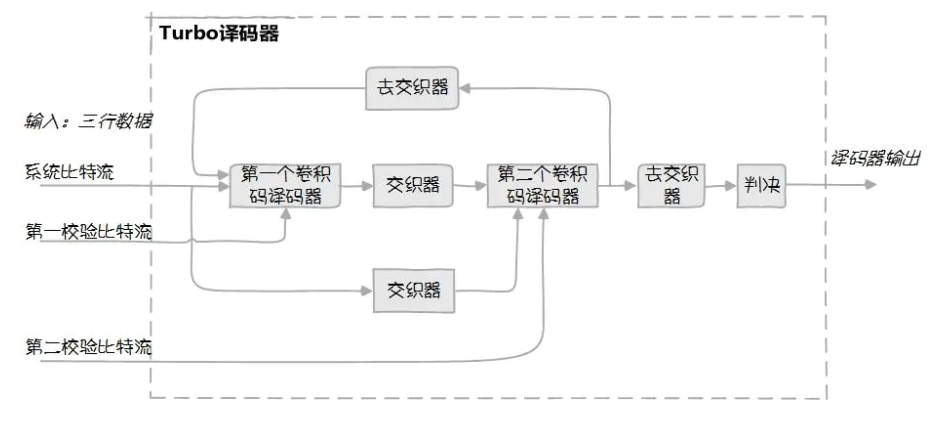
也可表示为

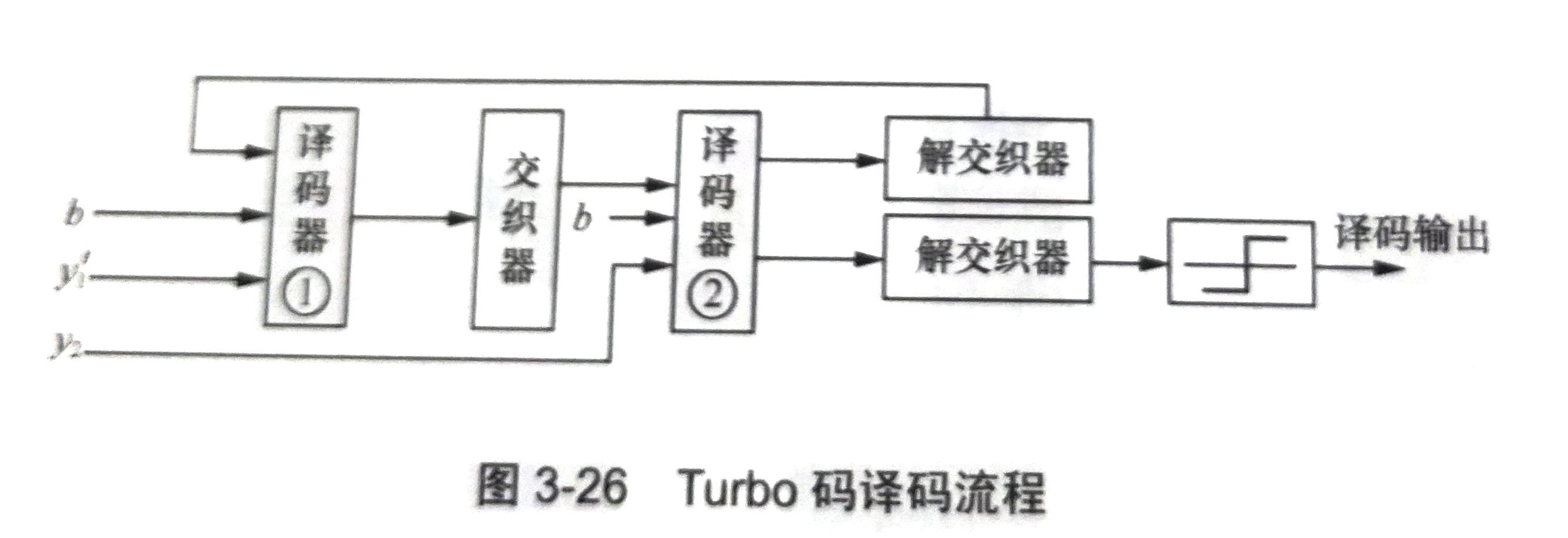
LDPC码

低密度奇偶校验 LDPC码本质上仍是线性分组码，并且是具有奇偶校验等式的线性分组码。LDPC很早已经被提出，但早期缺乏可行的译码算法，计算复杂性高，如今出现高效灵活的并行译码架构后，译码复杂度降低，才得以应用

对于$(n,k)$分组码，其校验信息长度为$m=n-k$，校验矩阵${\mathbf{H}}_{(n-k)\times n}$与合法码字行向量${\mathbf{C}}_{1\times n}^{\prime }$满足$\mathbf{H}({\mathbf{C}}^{\prime }{)}^T=0$

• LDPC码就是校验矩阵$\mathbf{H}$为稀疏矩阵的分组码，故称“低密度”-
• 常用因子图/Tanner图描述LDPC码，与校验矩阵$\mathbf{H}$一一对应
  $\mathbf{H}$的$n$列对应因子图上的$n$个信息节点/变量节点；
  $\mathbf{H}$的$m=n-k$行对应因子图上的$m=n-k$个校验节点（$\mathbf{H}{\mathbf{r}}^T={\mathbf{s}}^T$，其中${\mathbf{s}}_{1\times (n-k)}$相当于伴随式）；
  

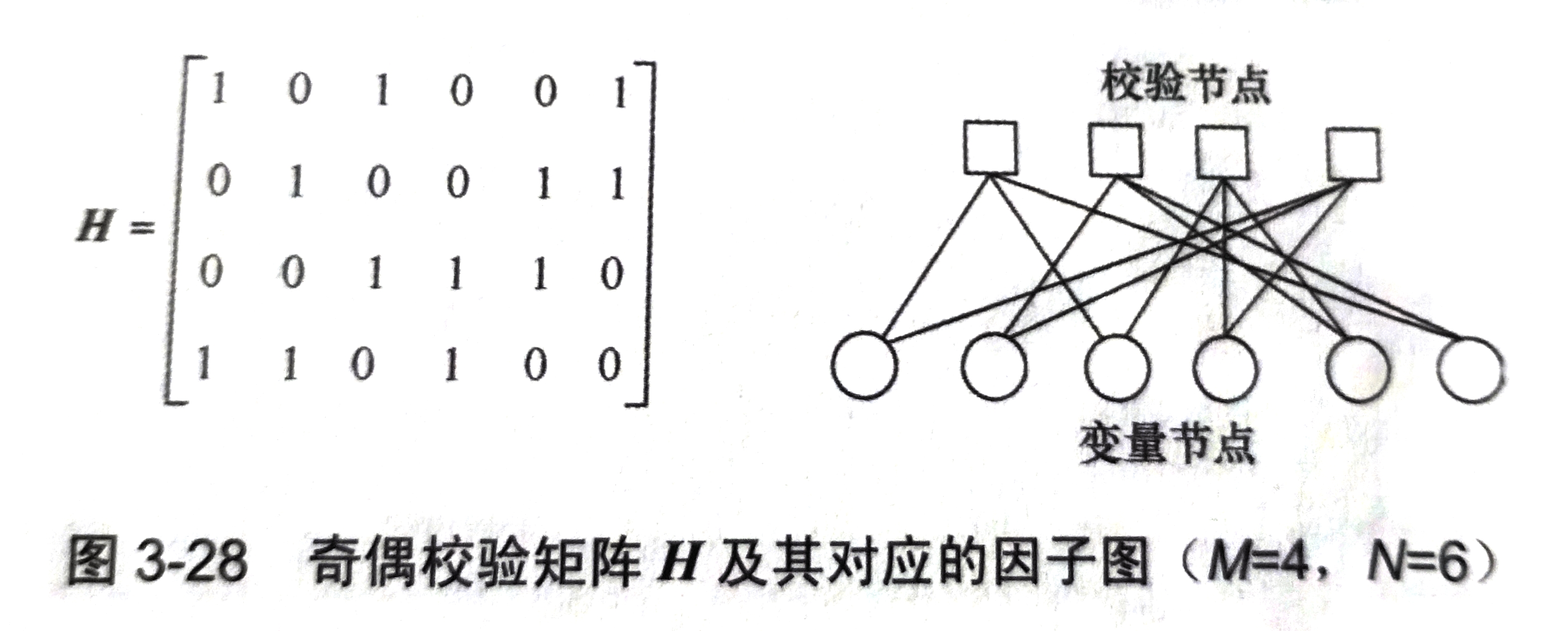
“低密度”是指LDPC的$\mathbf{H}$矩阵中1元素很少，从而Tanner图中的连接数也很少

本来从编码的角度看，基于校验矩阵的线性分组码，在编码时需要大量迭代（与码字大小的平方成正比）；但LDPC码的特殊设计保证了在不牺牲性能的同时降低了编译码复杂度

LDPC码使用全0或循环子矩阵（移位识别矩阵）构造奇偶校验矩阵

Polar码

Polar码是第一种被严格证明达到香农极限的信道编码，核心是信道极化理论（不同信道对应的极化方法有区别）

• 信道极化：对于一组独立的二进制对称输入离散无记忆信道，通过信道编码，可使各个子信道呈现不同的可靠性
  信道极化包括信道组合和信道分解两部分
  
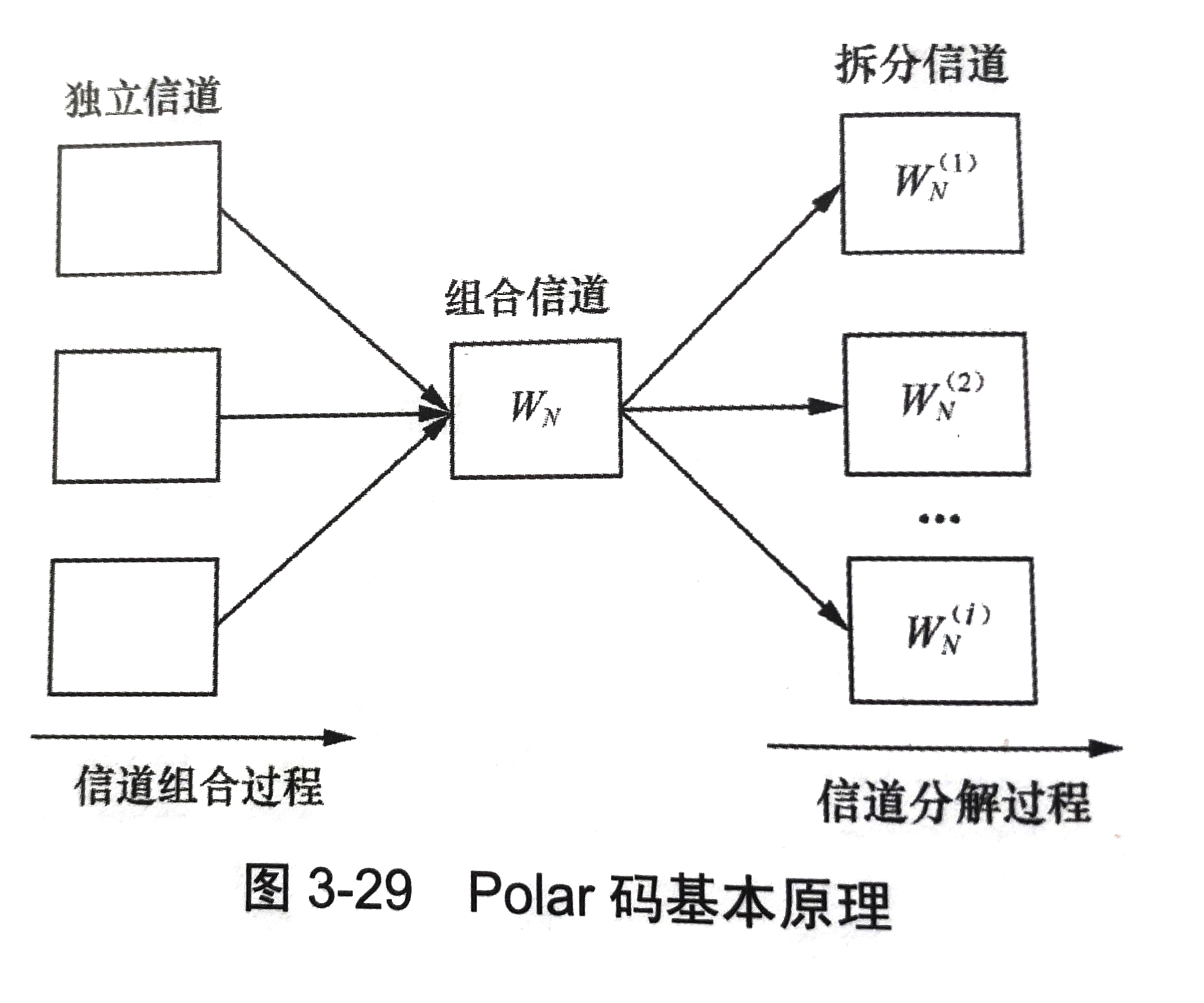
• 组合信道数目趋于无穷大时，出现极化，子信道向两个极端发展：一部分信道趋于无噪信道（传输速率达到信道容量），另一部分则趋于全噪信道（传输速率为0的）
• Polar码策略就是用无噪信道传输用户信息，全噪信道传输约定的信息/不传信息
• 由于发送时已知信道分布，并且只将有用信息放在“无噪信道”，译码使用改进的串行抵消列表SCL算法，复杂度低，且接近最大似然ML译码性能

Polar码优点：性能增益高（对于特定误码率要求，所需的信噪比更低）、可靠性高（没有误码平层）、译码复杂度低

最后

以上就是鲜艳紫菜最近收集整理的关于通信原理学习笔记4：信道编码、分组码、卷积码、现代信道编码（Turbo码、LDPC码、Polar码）的全部内容，更多相关通信原理学习笔记4内容请搜索靠谱客的其他文章。