文章目录
- 【 1. 同步计数器 】
- ① 同步二进制计数器
- 同步二进制加法计数器
- 74161 十六进制四位二进制加法计数器
- 74163
- 同步二进制减法计数器
- 同步二进制加/减计数器
- 单时钟方式 74191
- 双时钟方式 74193
- ② 同步十进制计数器
- 同步十进制加法计数器
- 74160
- 74162
- 同步十进制减法计数器
- 同步十进制加减计数器
- 【 2. 异步计数器 】
- ① 异步二进制计数器
- 异步二进制加法计数器
- 异步二进制减法计数器
- ② 异步十进制计数器
- 异步十进制加法计数器
- 【 3. N进制计数器→M进制计数器 】
- ① N>M
- 异步置零
- 同步置零
- 同步置数
- ② N
- 计数器的容量(计数器的模):时序中实际的状态个数。=2n
- n位二进制计数器中能计到的最大数=2n-1
【 1. 同步计数器 】
① 同步二进制计数器
同步二进制加法计数器
原理
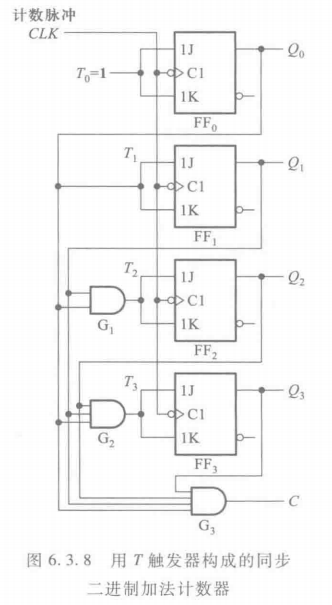
4位二进制同步加法计数器
方程
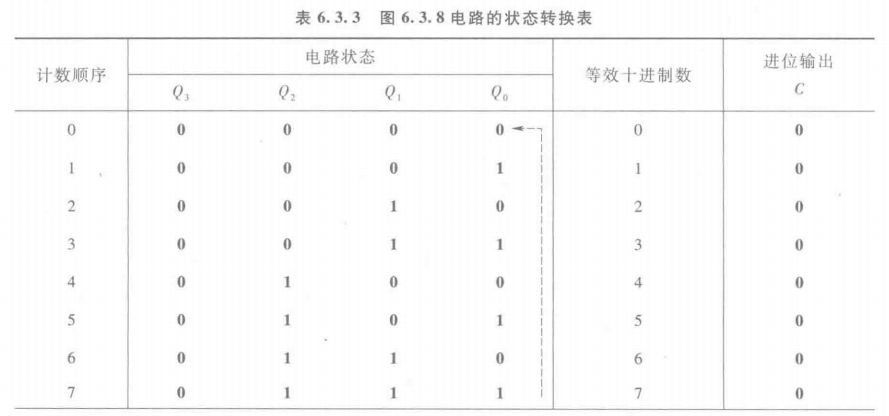
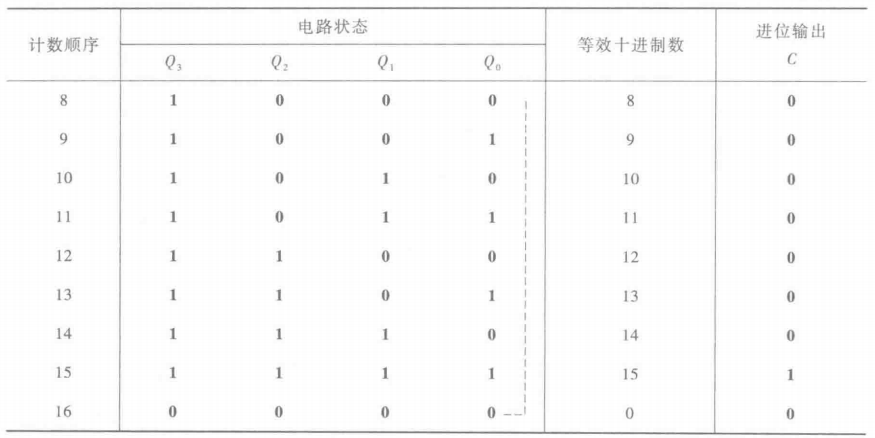
状态转换表
( 利用第16个计数脉冲到达时C端电位的下降沿可作为向高位计数器电路进位的输出信号 )
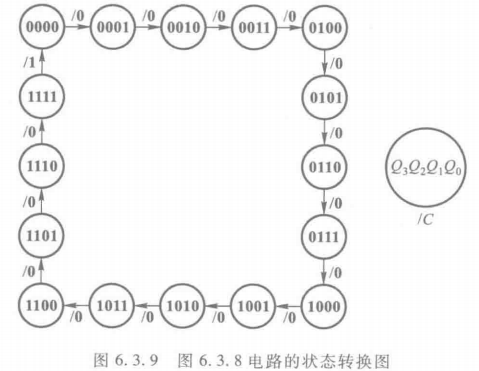
状态转换图
每输入16个脉冲,触发器状态循环一次,并且输出端C产生一个进位信号,故为16进制计数器
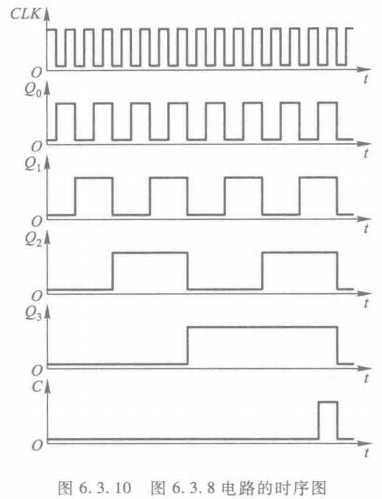
时序图
从时序图中可以看出,若计数输入脉冲的频率为f0,则Q0、Q1、Q2、Q3输出端脉冲的频率将依次为 1 2 f 0 frac{1}{2}f~0~ 21f 0 、 1 4 f 0 frac{1}{4}f~0~ 41f 0 、 1 8 f 0 frac{1}{8}f~0~ 81f 0 、 1 16 f 0 frac{1}{16}f~0~ 161f 0 。
即分频功能。
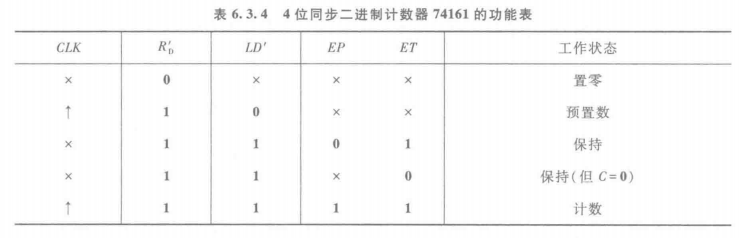
74161 十六进制四位二进制加法计数器
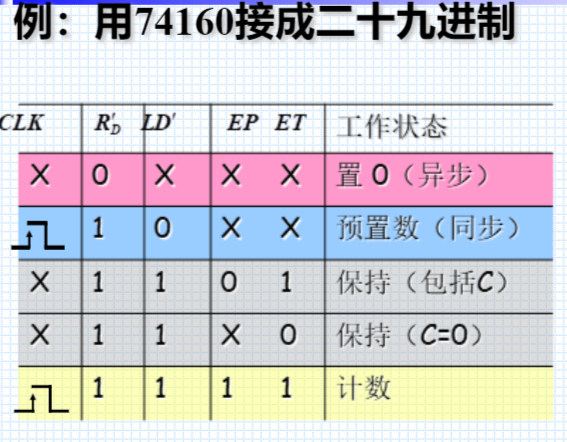
具有加法计数、同步预置数、异步置0、保持功能。
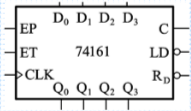
LD’ 预置数控制端
D0 ~ D3 数据输入端
C 进位输出端
RD’ 异步置零(复位)端
EP、ET 工作状态控制端
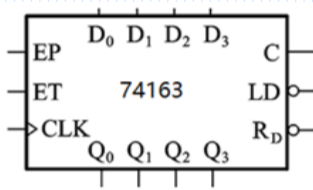
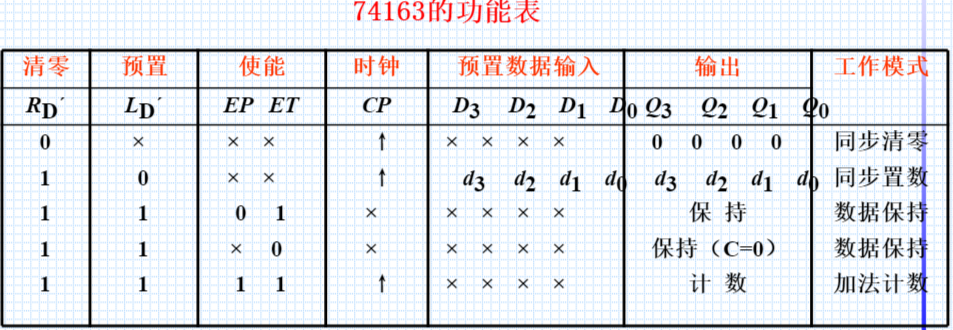
74163
具有同步清零、同步并行预置数、计数、保持功能。
同步二进制减法计数器
原理
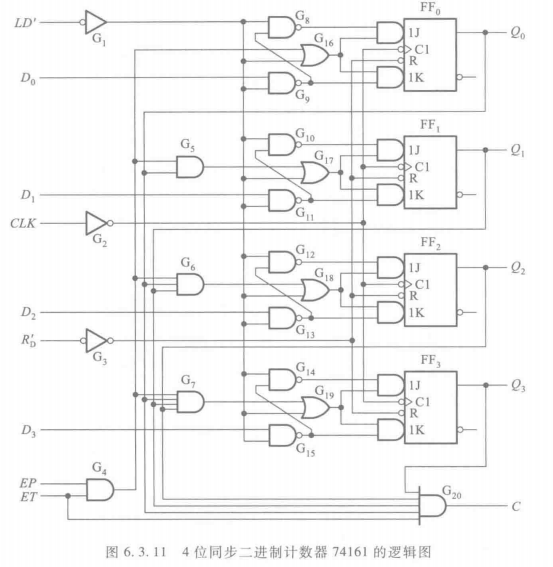
逻辑图
同步二进制加/减计数器
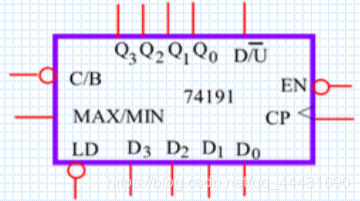
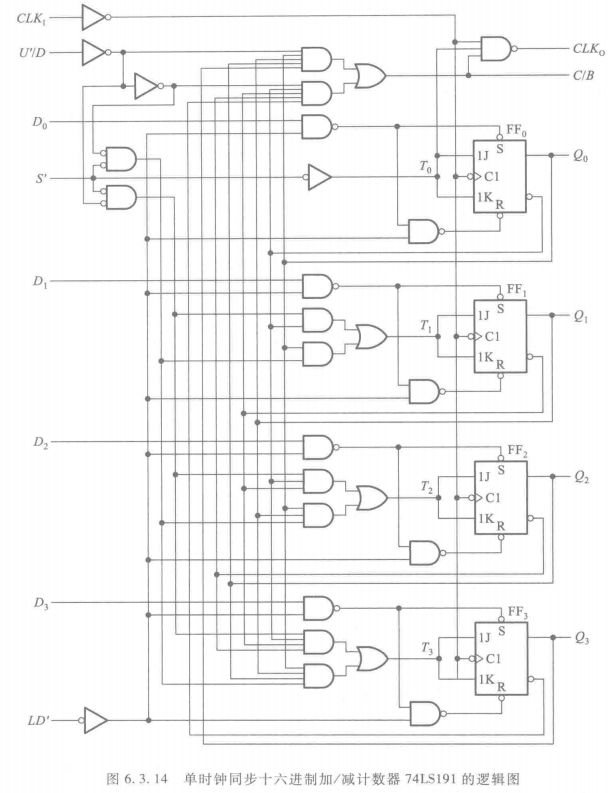
单时钟方式 74191
74LS191功能:异步置数、保持、加/减计数
单时钟定义
由加/减控制电平的高低来决定加计数还是减计数
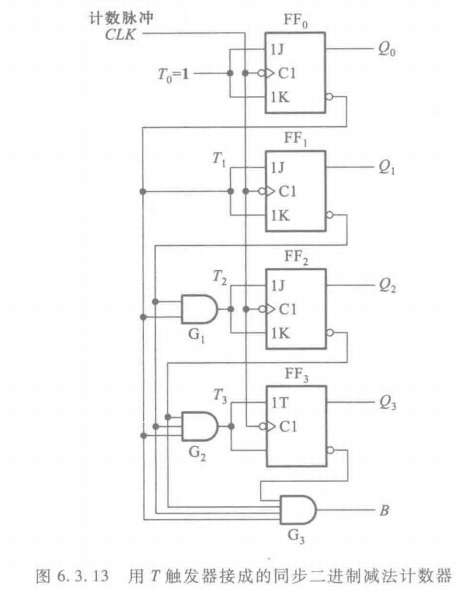
逻辑图
采用T触发器
方程
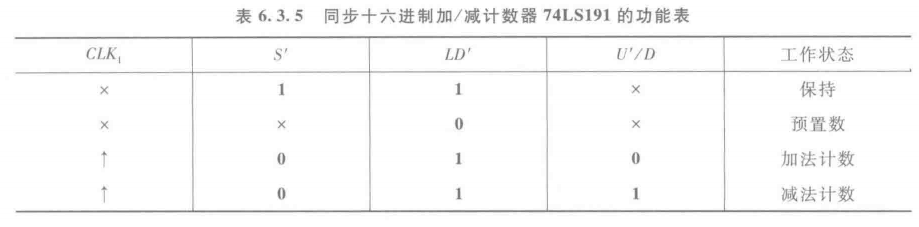
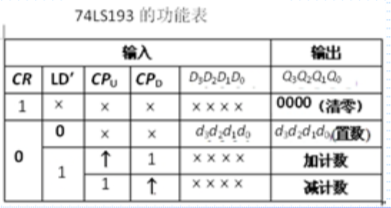
功能表
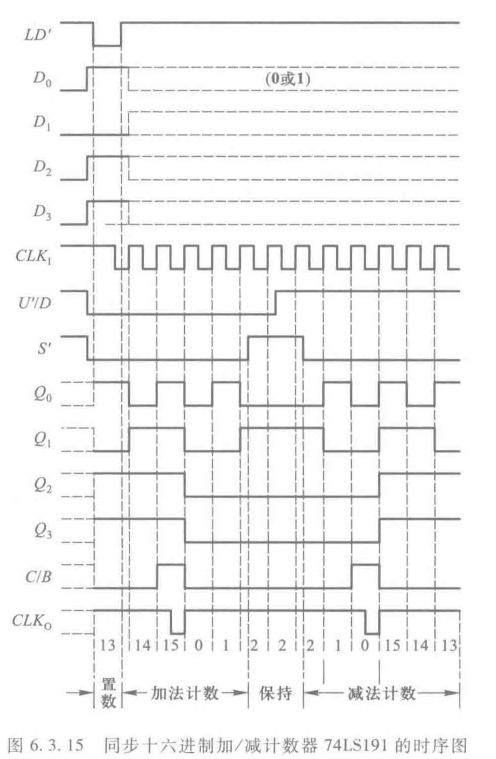
时序图
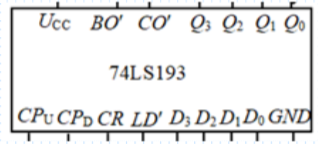
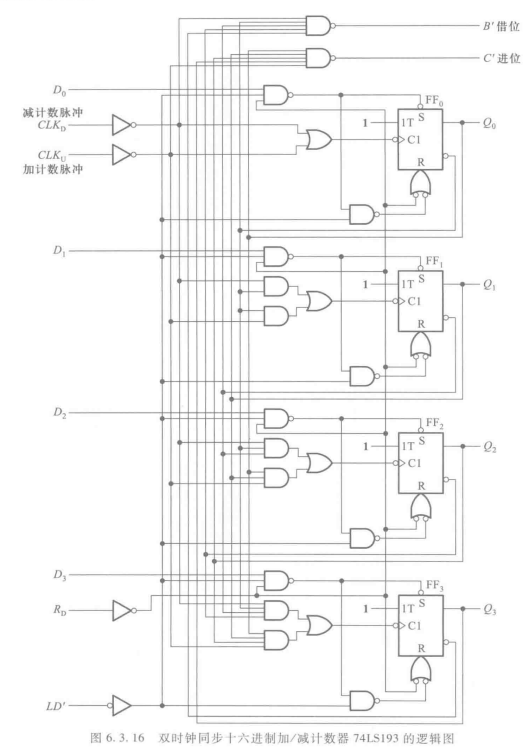
双时钟方式 74193
74LS193功能:异步置零、异步置数、保持、加/减计数
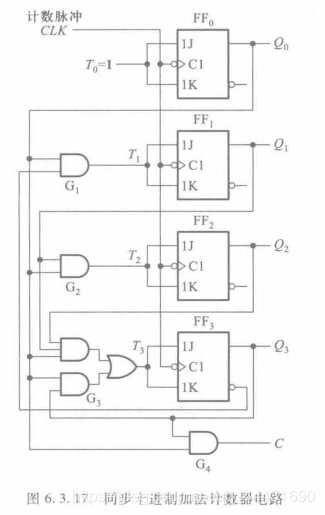
逻辑图
采用 T’ 触发器( 即T触发器的T=1)
方程
功能表
② 同步十进制计数器
同步十进制加法计数器
原理
逻辑图
驱动方程
状态方程
状态转换表
状态转换图(可自启动)
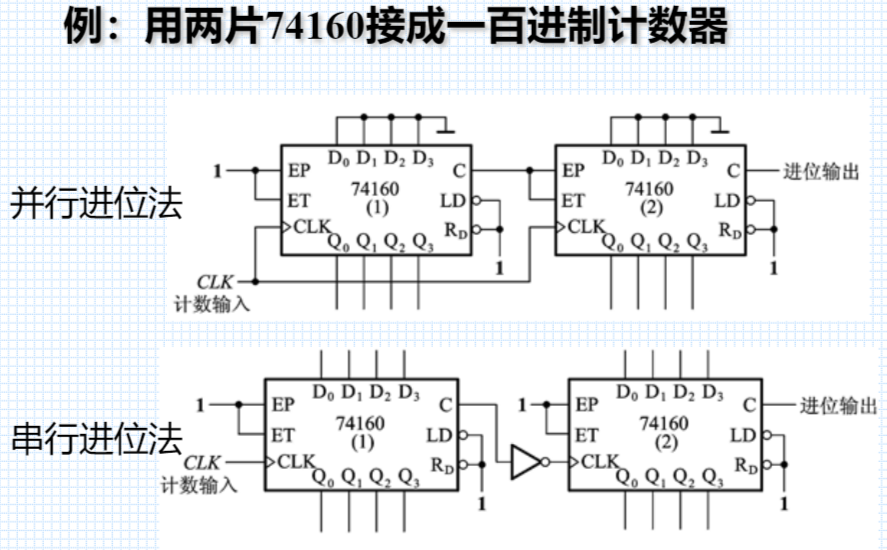
74160
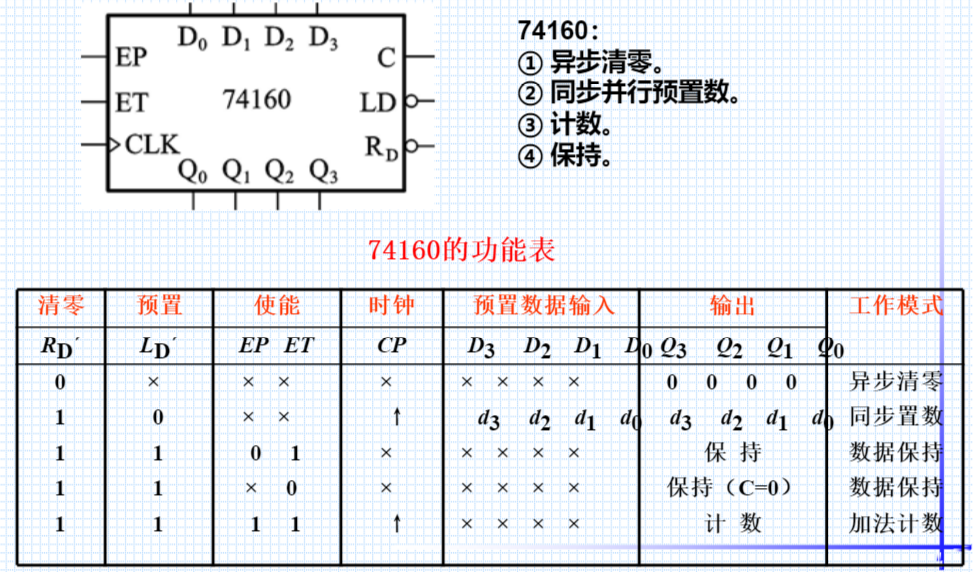
74162
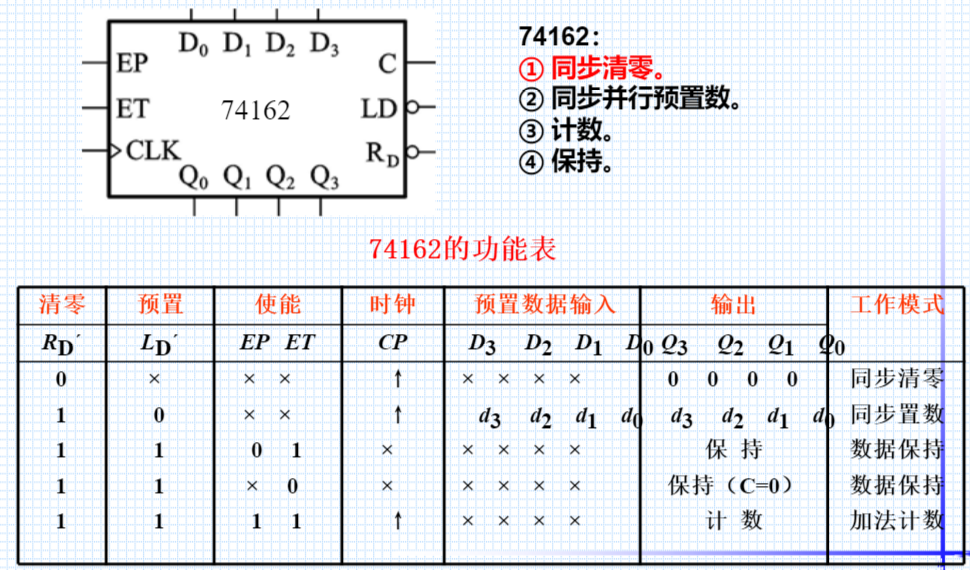
同步十进制减法计数器
原理
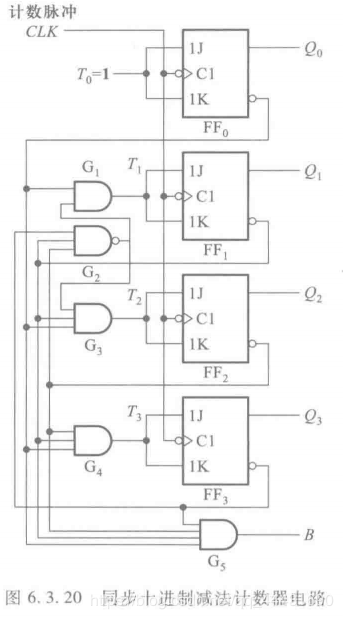
逻辑图
驱动方程
状态方程
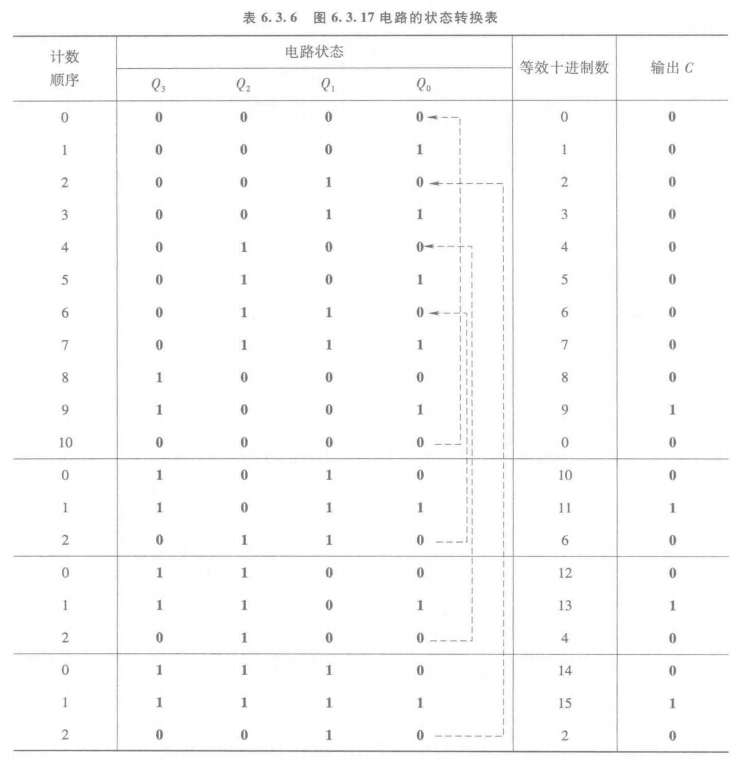
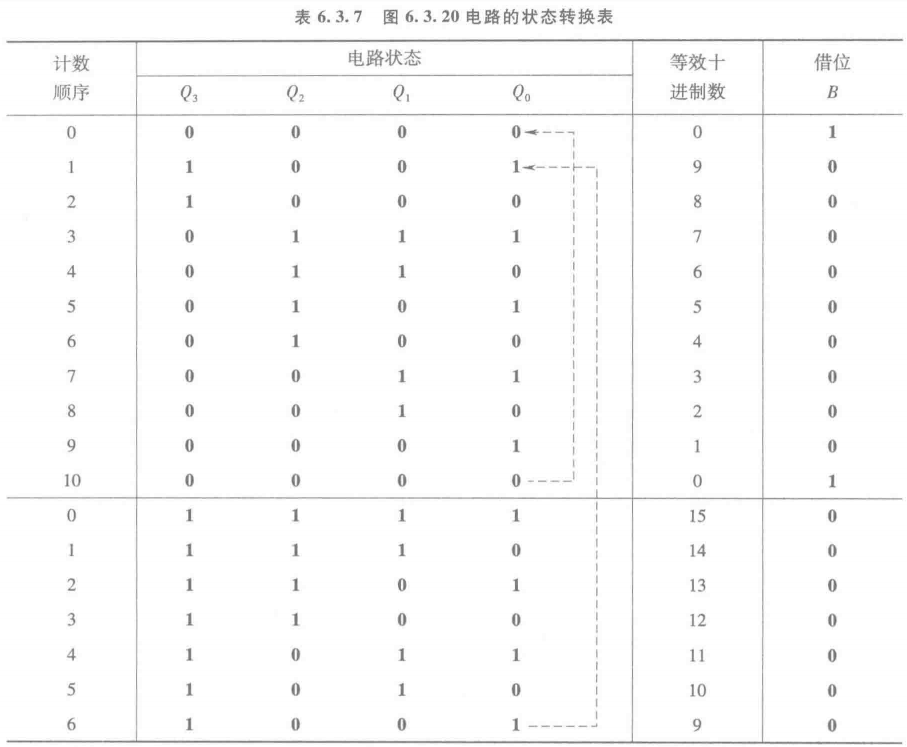
状态转换表
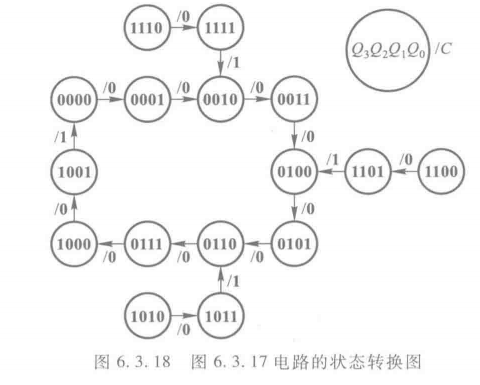
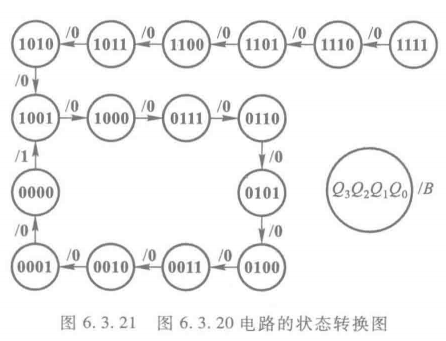
状态转换图
同步十进制加减计数器
单时钟类型:74LS190、74LS168、CC4510
双时钟类型:74LS192、CC40192
【 2. 异步计数器 】
① 异步二进制计数器
异步二进制加法计数器
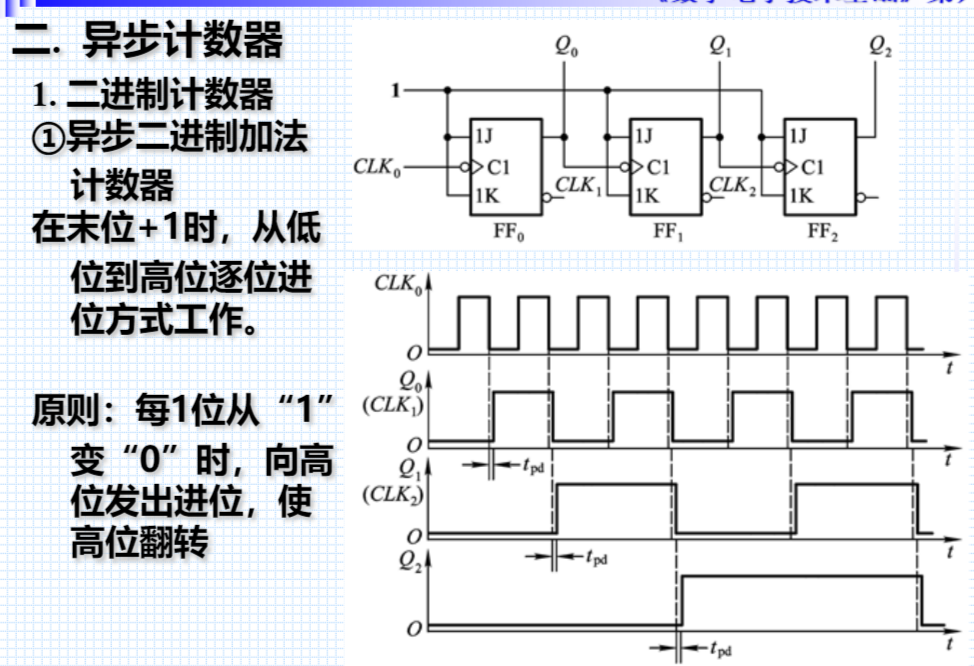
异步二进制减法计数器
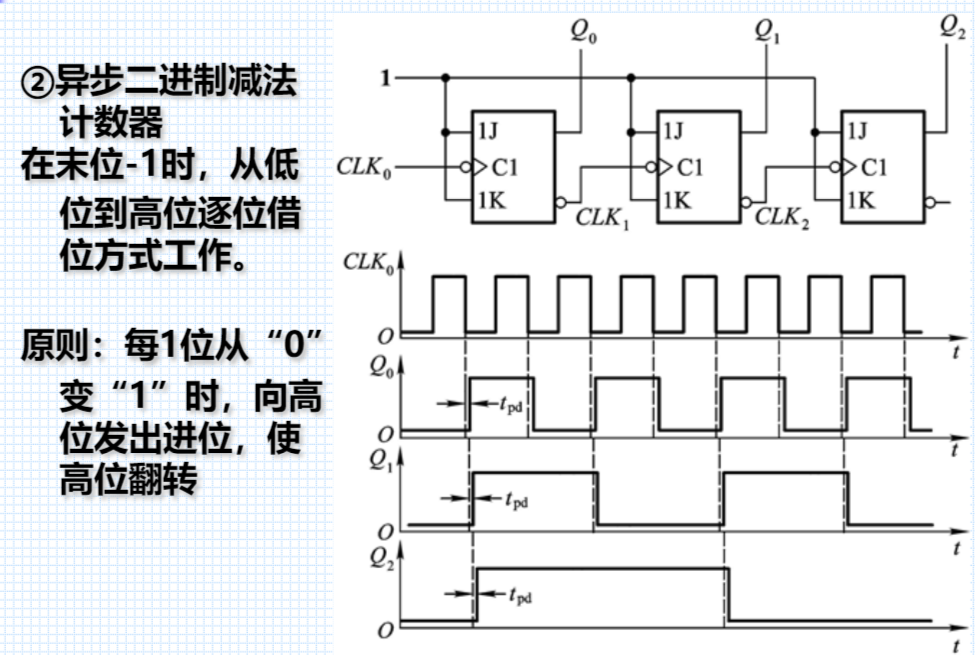
② 异步十进制计数器
异步十进制加法计数器
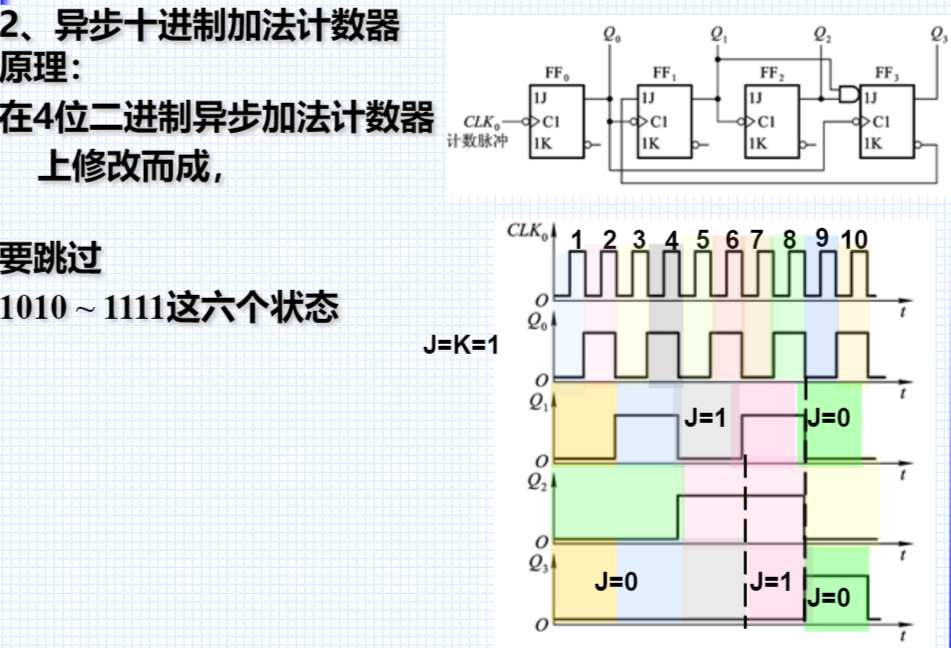
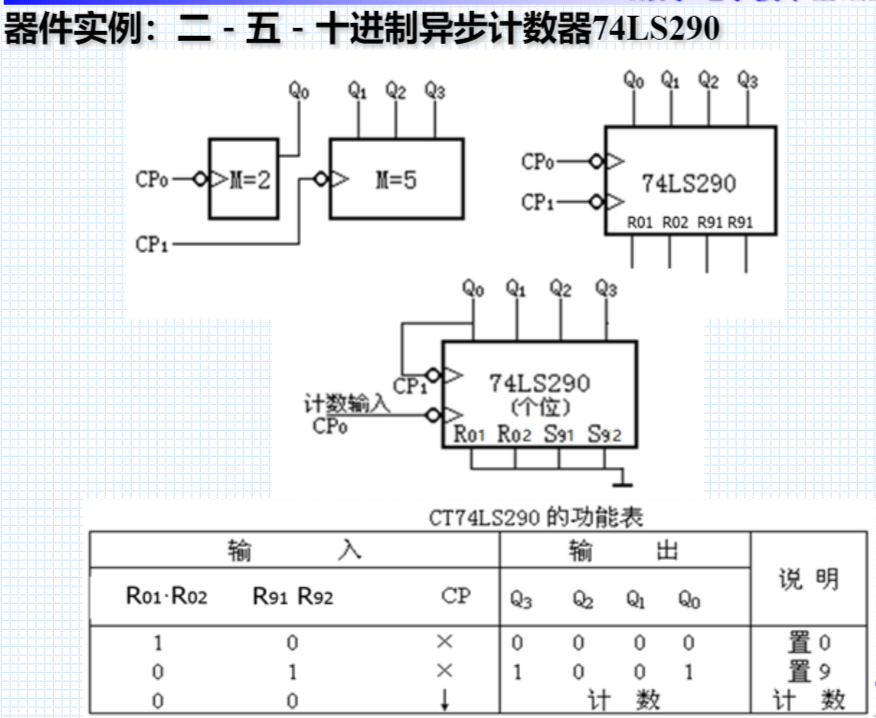
【 3. N进制计数器→M进制计数器 】
① N>M
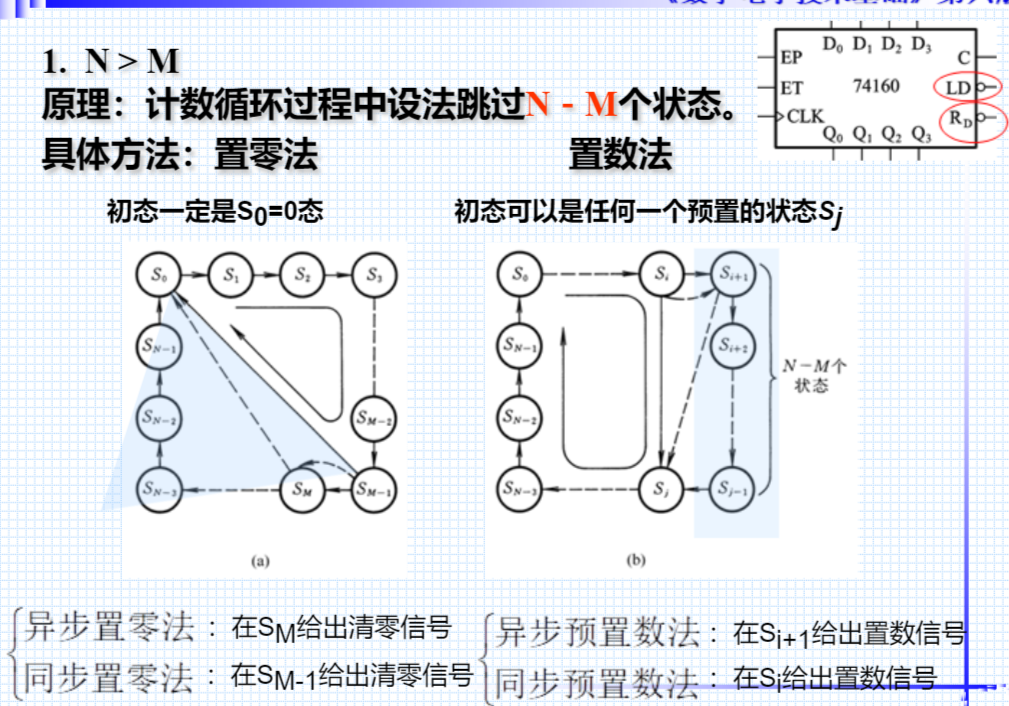
异步置零
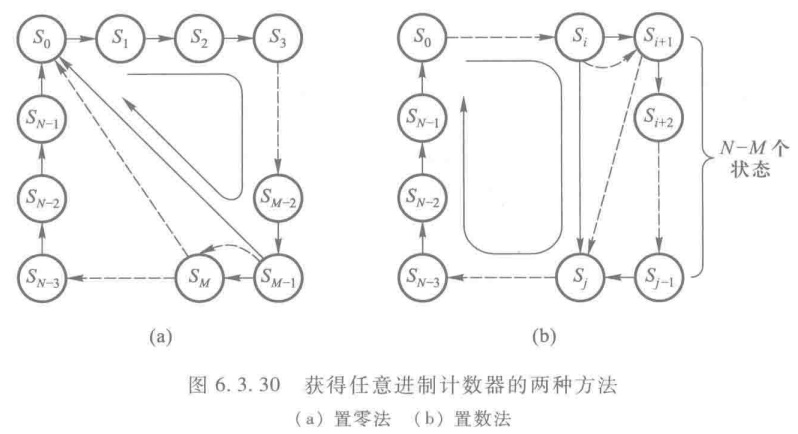
如图6.3.30(a)虚线
从S0计数到SM时立即又异步 (时间极短) 被置成S0,故SM状态不稳定(稳定状态循环中不包括这个状态)。
同步置零
如图6.3.30(a)实线
从S0计数到SM-1时同步(等到下个时钟) 被置成S0(稳定状态循环中包括这个状态)。
异步置数
如图6.3.30(b)虚线
从S0计数到Si+1时异步(时间极短) 被置成Sj(其中快进了N-M个状态),再计数到S0。故Si+1状态不稳定(稳定状态循环中不包括这个状态)。
.
同步置数:
如图6.3.30(b)实线
从S0计数到Si时同步(等到下个时钟) 被置成Sj(其中快进了N-M个状态),再计数到S0。Si状态不稳定(稳定状态循环中包括这个状态)
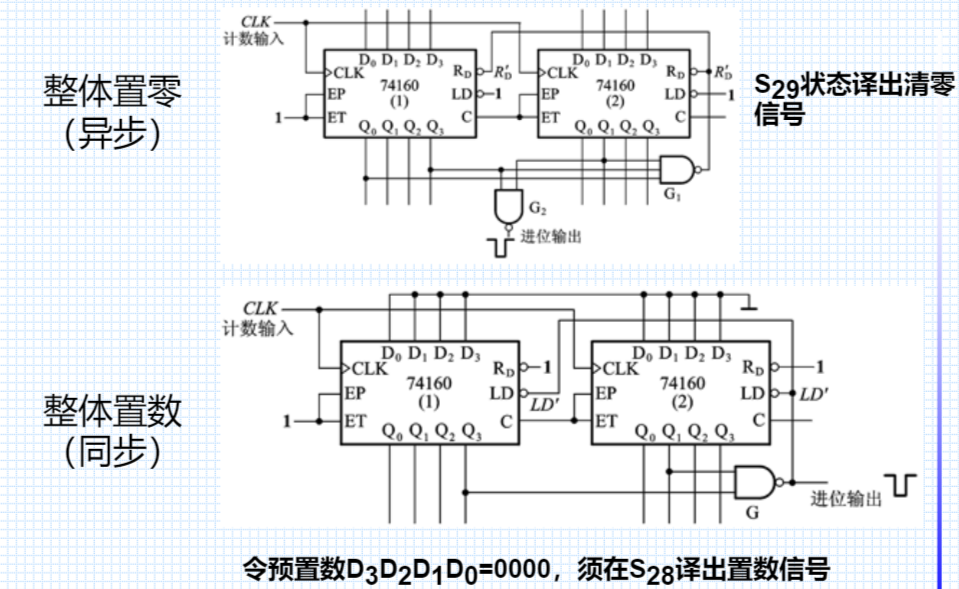
异步置零
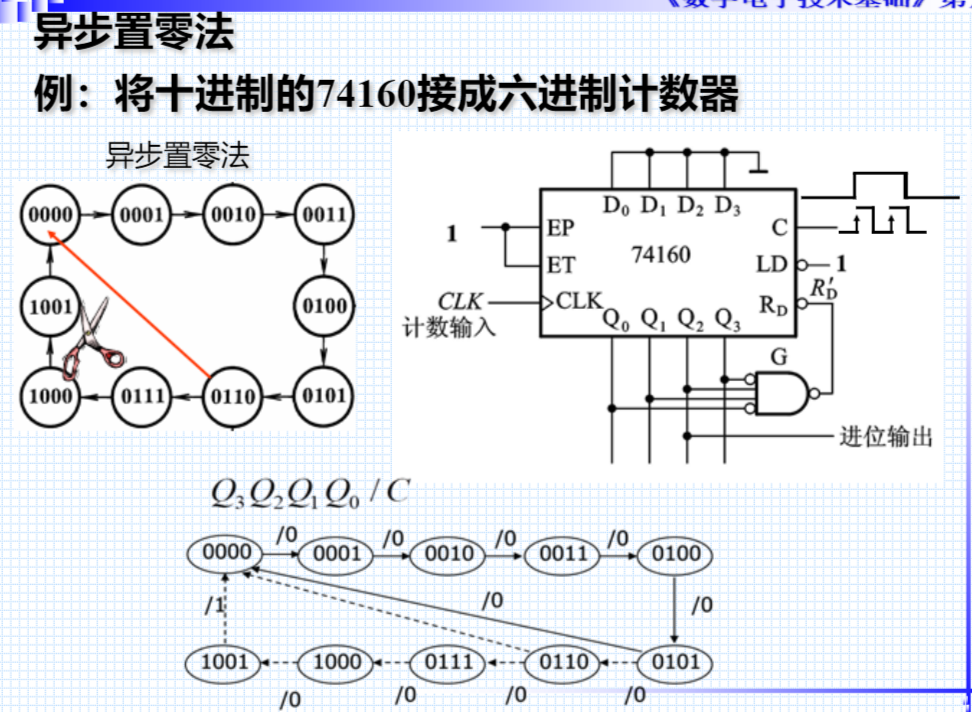
同步置零
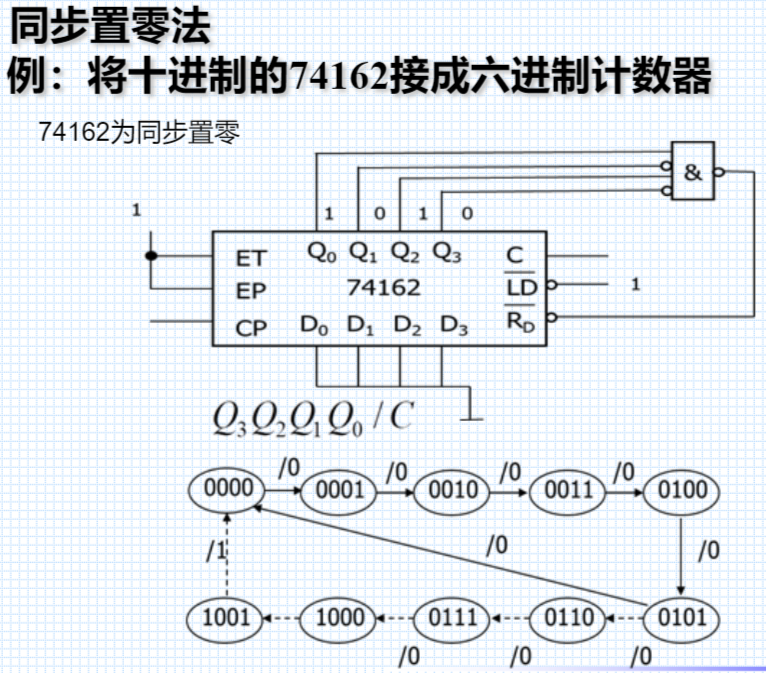
同步置数
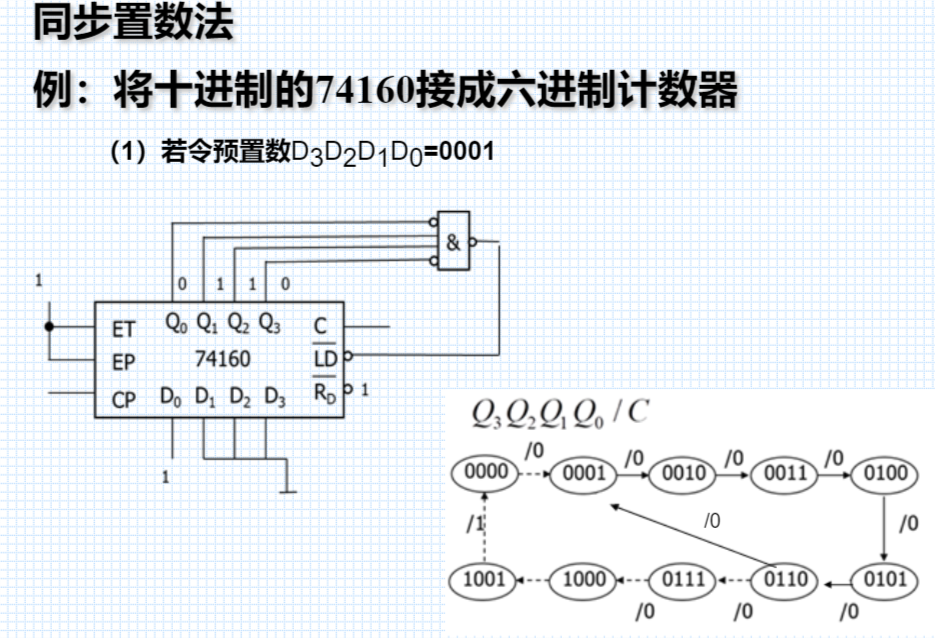
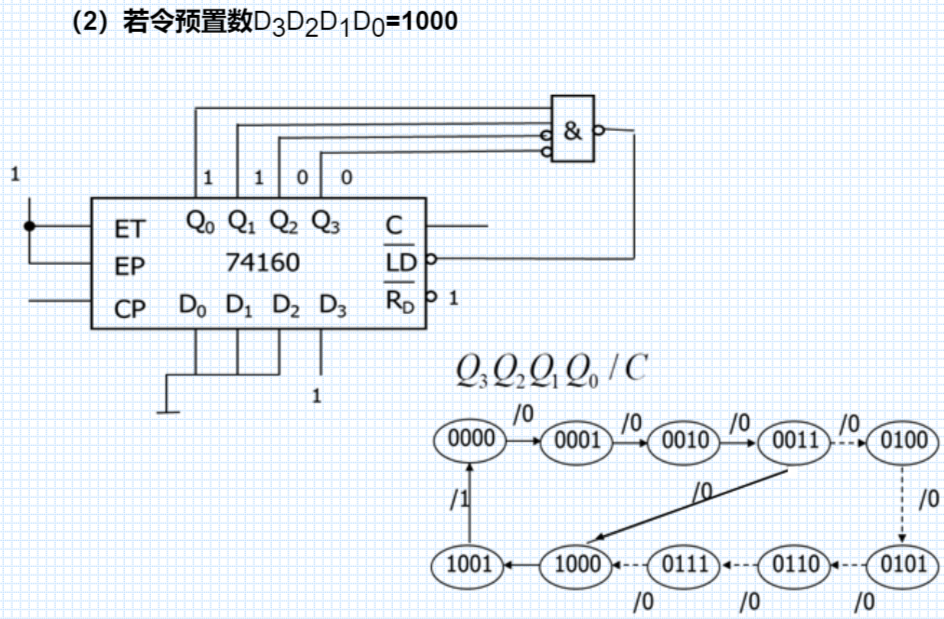
② N<M

M=N1xN2
M<NxN
【 4. 移位寄存器型计数器 】
① 环形计数器
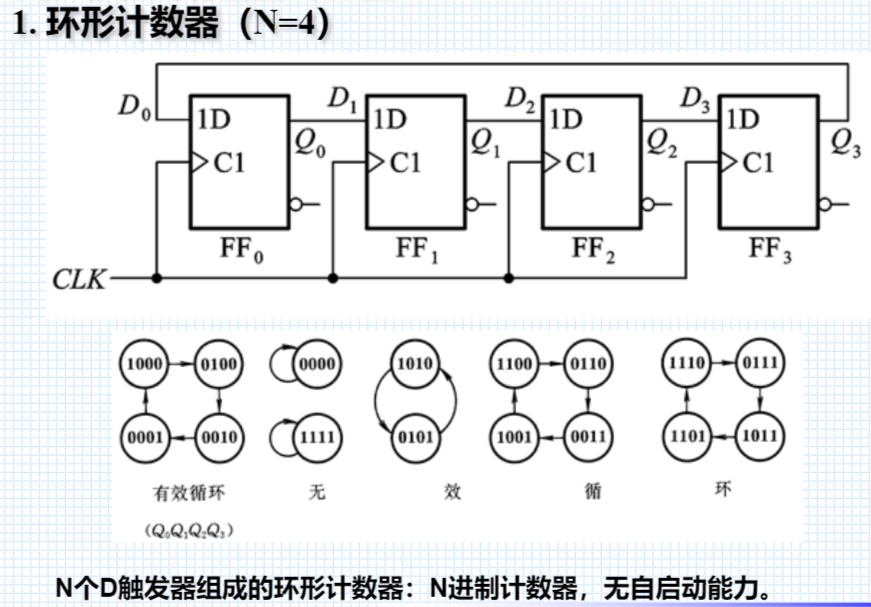
② 扭环形计数器
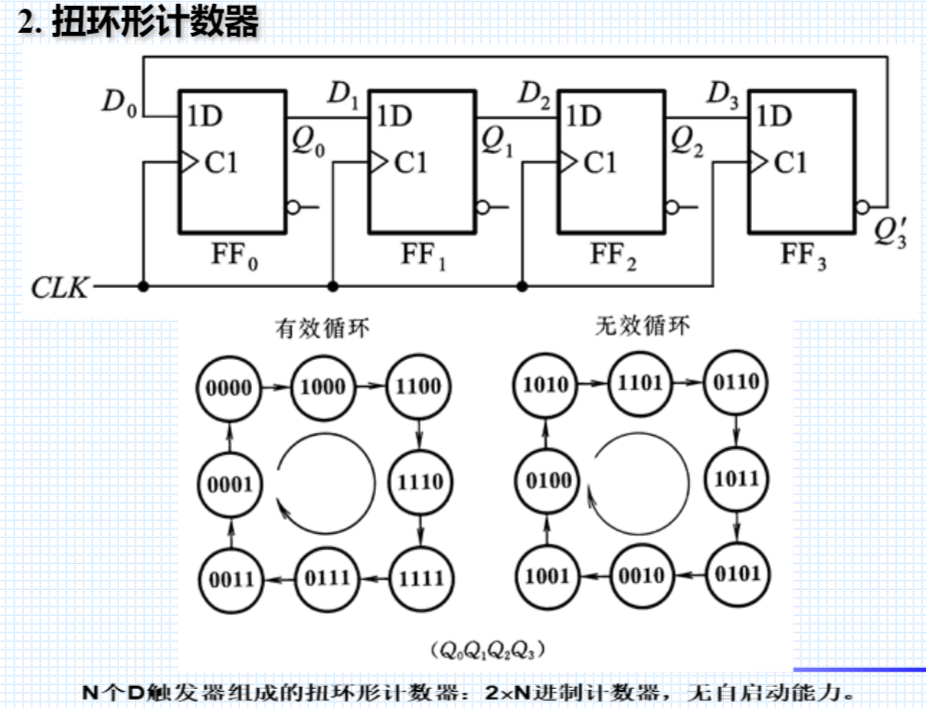
【 5. 计数器应用 】
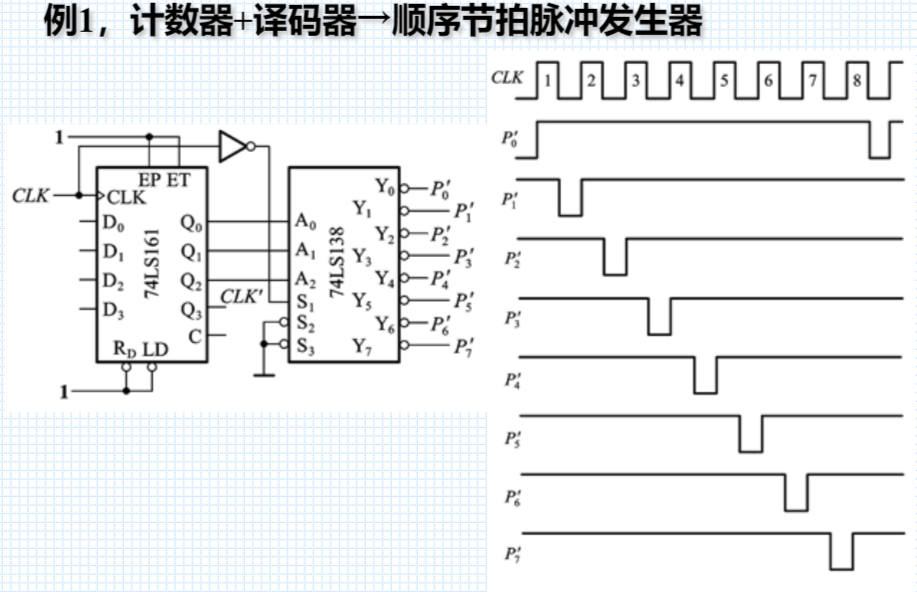
① 顺序节拍脉冲发生器
74LS138译码器的 S1、S2、S3可视为总开关,当三者同时有效时,方可正常工作,否则其8个输出端均为1。
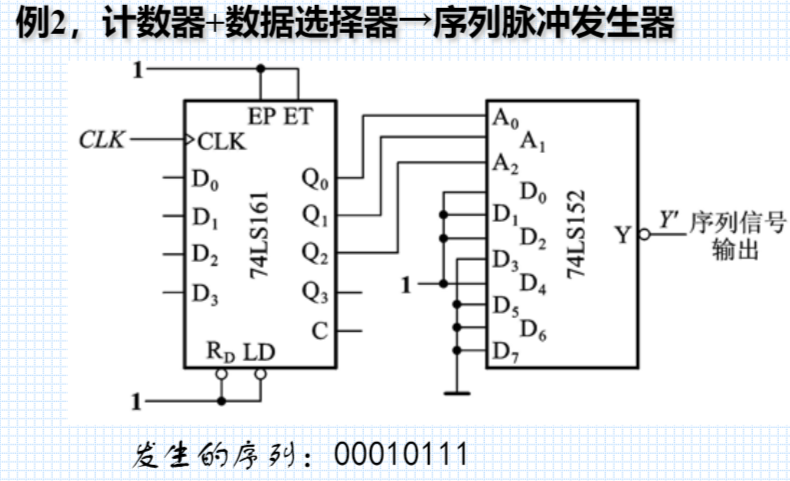
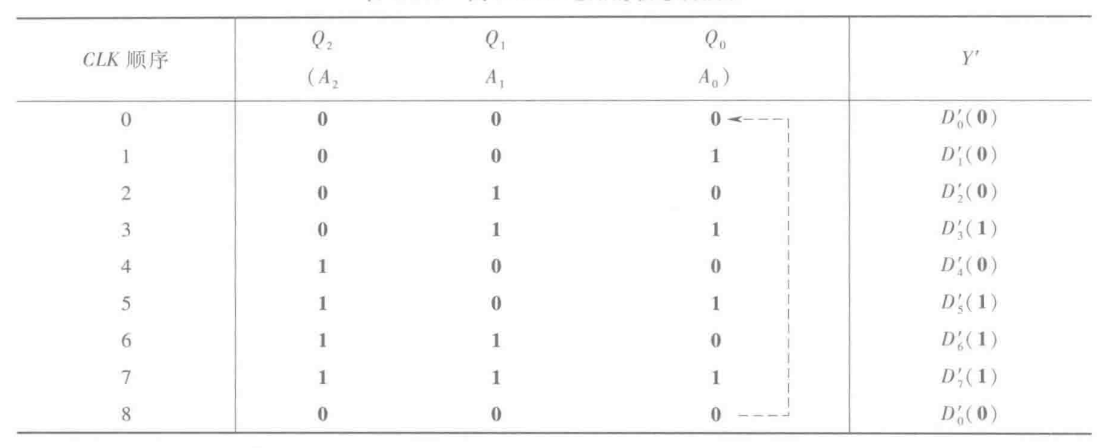
② 序列脉冲发生器
74LS152为8选1数据选择器
最后
以上就是凶狠冬日最近收集整理的关于计数器【 1. 同步计数器 】【 2. 异步计数器 】【 3. N进制计数器→M进制计数器 】【 4. 移位寄存器型计数器 】【 5. 计数器应用 】的全部内容,更多相关计数器【内容请搜索靠谱客的其他文章。








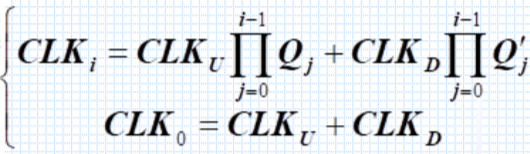



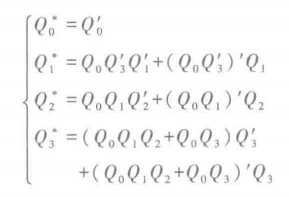

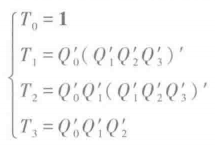
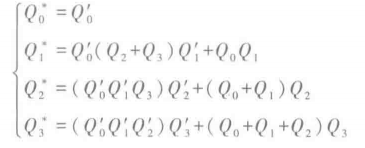
















发表评论 取消回复