同步置零和异步置零

同步置零、异步置零是相对于触发器内的数据的变化而言的。所谓的同步和异步其实就是是否和时钟脉冲同步。置零即清零，同步置零就是一定要等到时钟脉冲CLK有效（等于0或者等于1）的时候才能清零，异步清零就是不用看时钟脉冲CLK，只要给置零端信号就能立刻实现置零。同步要考虑时钟脉冲，异步不考虑时钟脉冲。
 

同步预置数和异步预置数

同步置数在输入端获得置数信号后，只是为置数创造了条件，还需要再输入一个计数脉冲CP，计数器才能将预置数置入。异步置数与时钟脉冲没有任何关系，只要异步置数控制端出现置数信号，并行数据便立刻被置入。

一. 移位寄存器

移位寄存器具有存储代码、移位、数据转换、数值运算、数据处理等功能。

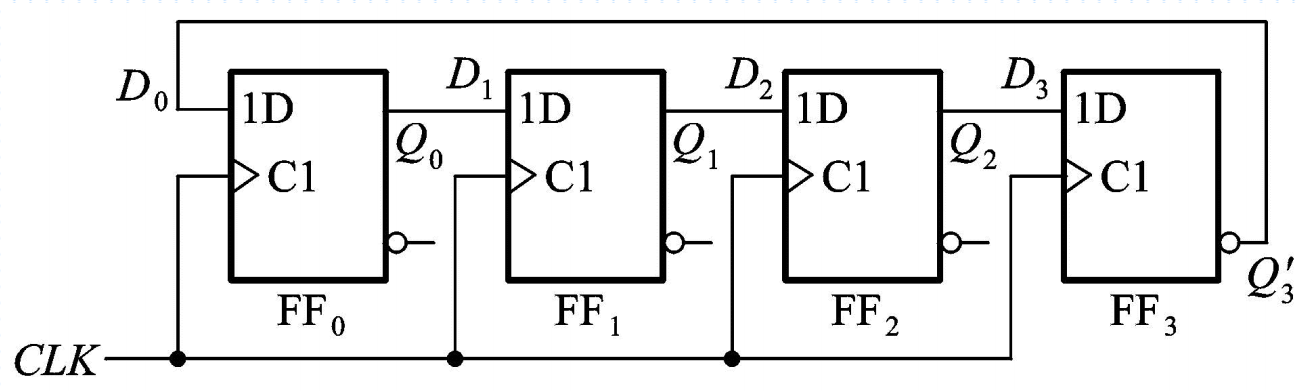
I. D触发器构成的4位移位寄存器

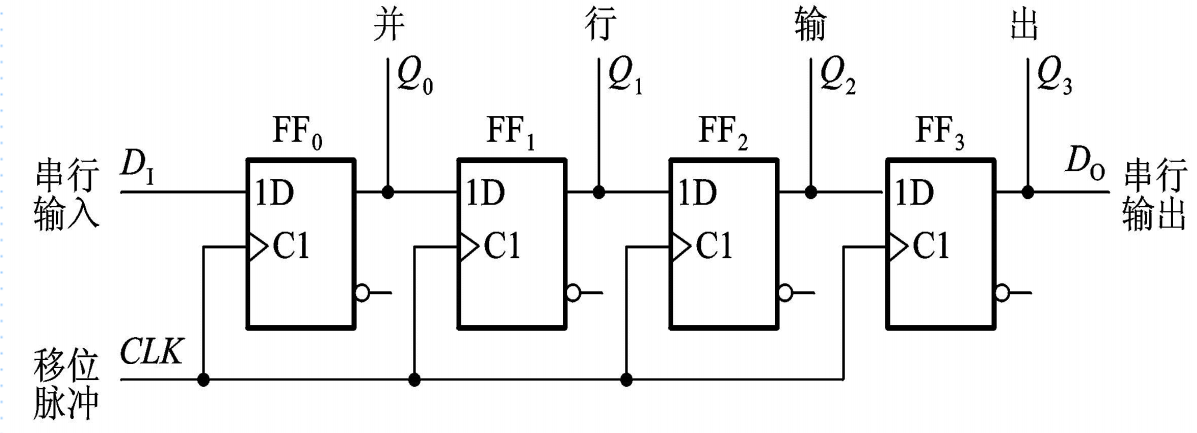
由边沿触发方式的D触发器组成的4位移位寄存器，第一个触发器的输入端D1接收输入信号，其余的每个触发器输入端D均与前一个触发器的输出端Q相连。其可以实现将原有的代码依次右移1位，利用这个性质还可以实现代码的串行-并行转换。

右移一位即乘2，左移一位即除以2。

【电路图】

II. 双向移位寄存器 74HC194

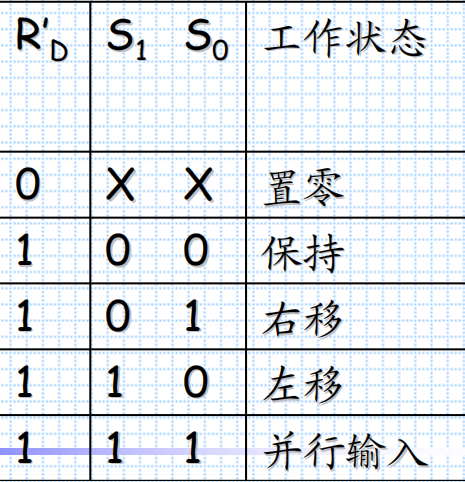
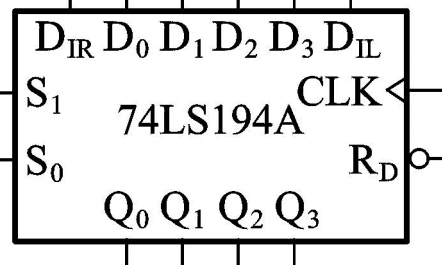
双向移位寄存器74HC194在普通移位寄存器的基础上，又增加了数据右移串行输入端DIR、数据左移串行输入端DIL、数据并行输入端D0 ~ D3、数据并行输出端Q0 ~ Q3、工作状态控制端S0和S1、异步置零端RD’。因此，74HC194具有左/右移、并行输入、保持、异步置零等功能。

【功能表】

【逻辑框图】

以74HC147为基础，可以利用多片74HC147接成多位双向移位寄存器。例如，用两片74HC147连接成八位双向移位寄存器，只需要将第一片的Q3连接至第二片的DIR、第二片的Q0连接至第一片的DIL、同时将两片的S0、S1、CLK和RD’分别并联即可。

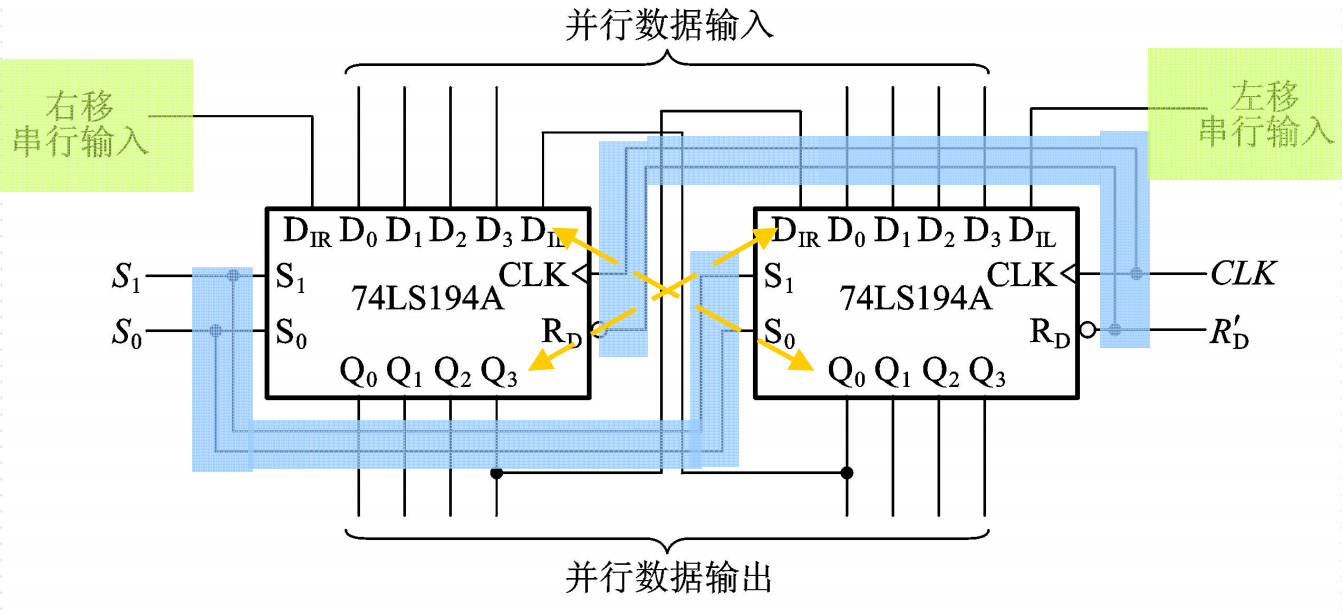
二. 计数器

计数器不仅能用于对时钟脉冲进行计数，还可以用于分频、定时、产生节拍脉冲、产生脉冲序列、进行数字运算等。

I. 同步计数器

i. 同步二进制计数器

1. 同步二进制加法计数器 74161

同步计数器由T触发器构成，每次的CLK信号到达时，使得该翻转的触发器的Ti=1，不该翻转的触发器的Ti=0。则加法计数器的第i位触发器的输入端的逻辑式为：

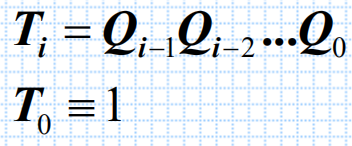
按照这个原理，我们可以接成4位二进制同步加法计数器。

【驱动方程】

T0 = 1
T1 = Q0
T2 = Q0 Q1
T3 = Q0 Q1 Q2

【状态方程】

Q0 * = Q0’
Q1 * = Q0 Q1’ + Q0’ Q1
Q2 * = Q0 Q1 Q2’ + (Q0 Q1)’ Q2
Q3 * = Q0 Q1 Q2 Q3’ + (Q0 Q1 Q2)’ Q3

【输出方程】

C = Q0 Q1 Q2 Q3

【状态转换图】

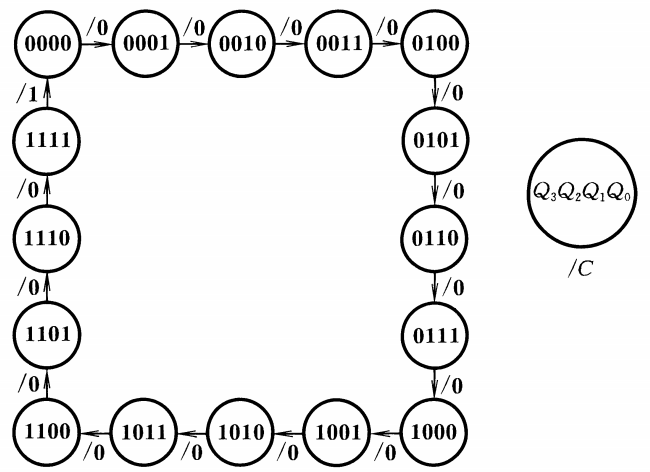
从状态转换图可以看出，同步二进制加法计数器每输入16个计数脉冲工作一个循环，并最终在Q3产生一个进位输出信号，因此同步二进制加法计数器又称为十六进制计数器。

【时序图】

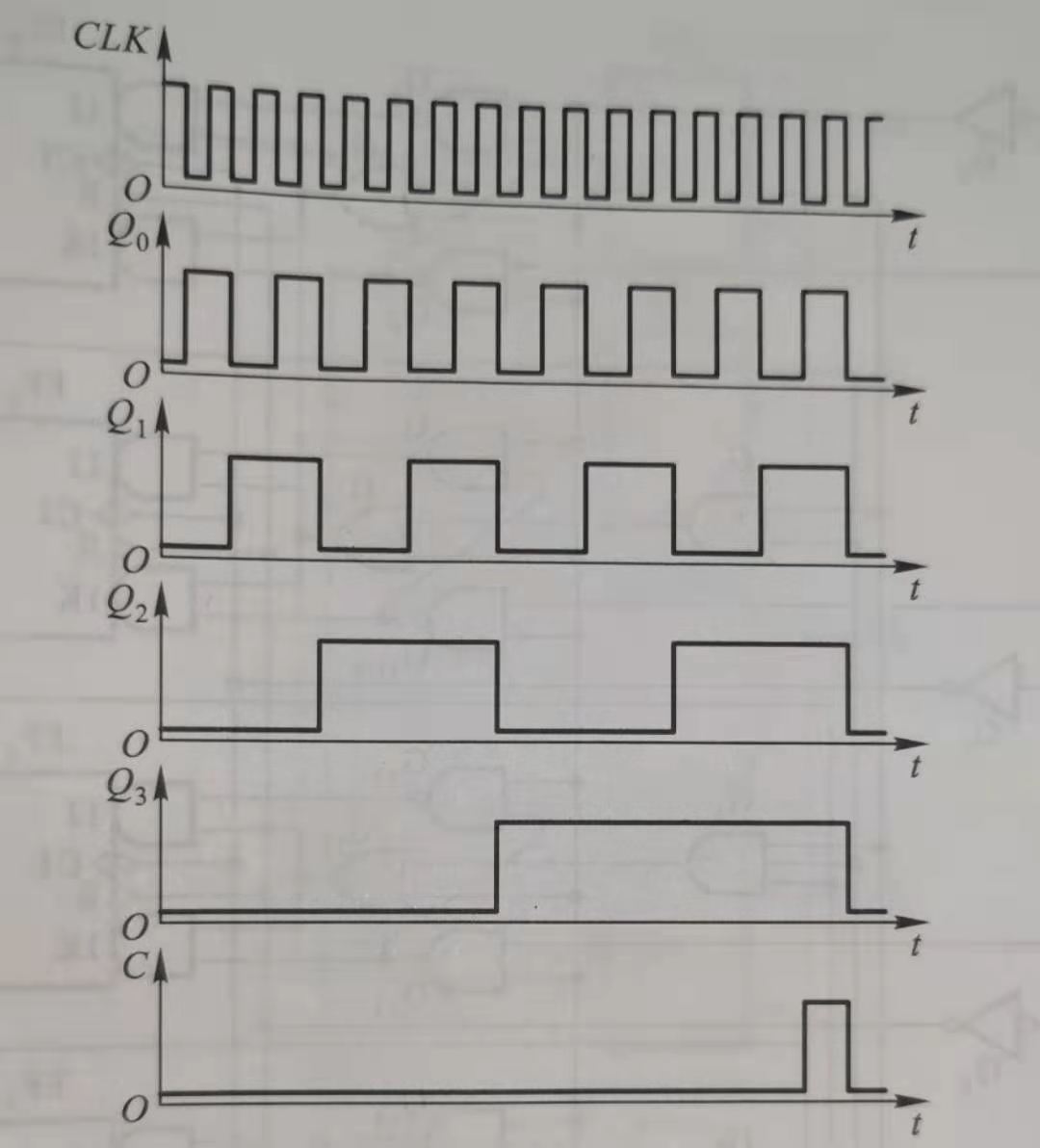
从时序波形图我们可以看出，同步二进制加法计数器具有分频功能。设输入脉冲的频率为f0，则Q0、Q1、Q2、Q3端输出脉冲的频率依次为 f0/2、f0/4、f0/8、f0/16。

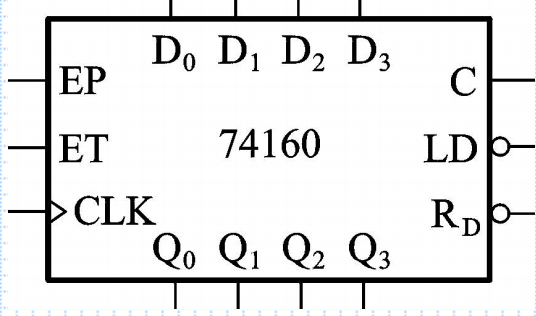
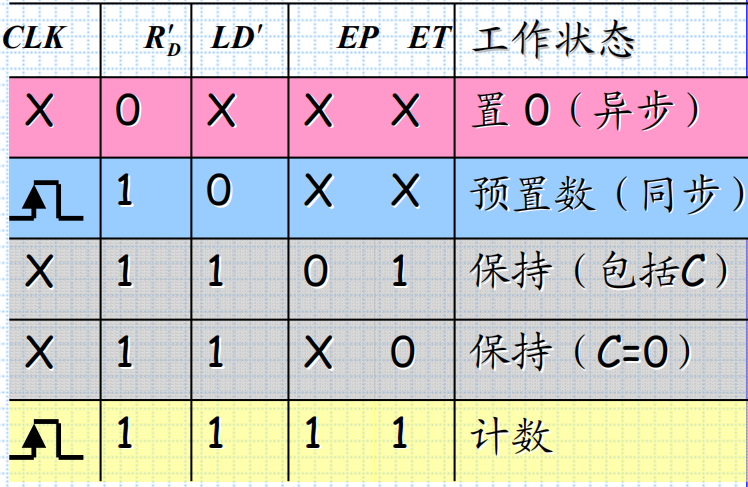
74161在此基础上还加入了同步预置数控制端LD’、数据输入端D0~D3、进位输出端C、异步置零端RD’、工作状态控制端EP和ET。

【逻辑框图】

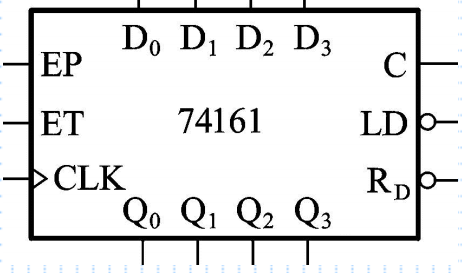
【功能表】

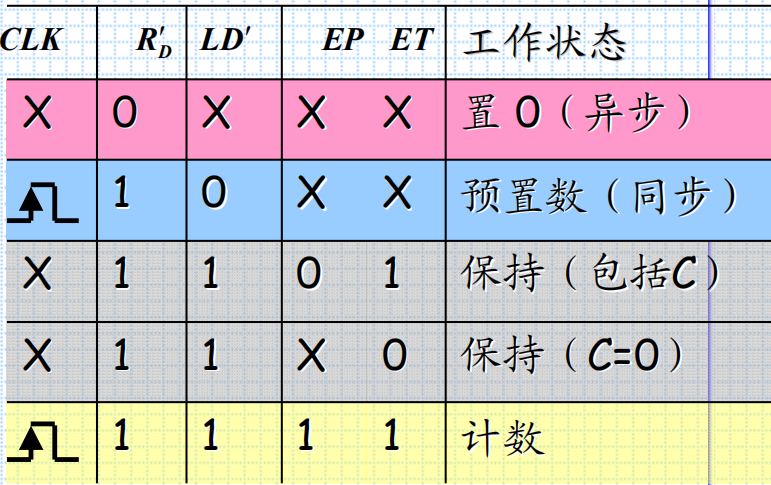
2. 同步二进制减法计数器

与加法计数器相反，减法计数器的第i位触发器的输入端的逻辑式为：

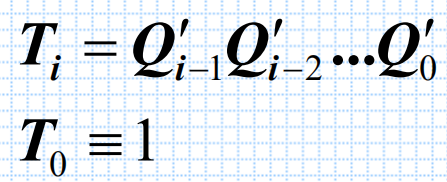
我们也可以像构成同步二进制加法计数器那样构成同步二进制减法计数器，在此不多赘述。
 

3. 同步加/减计数器 74LS191 74LS193

加减计数器实现了将加法计数器和减法计数器的电路的合并，有两种构成加减计数器的方式：单时钟方式和双时钟方式。
 

（1）单时钟方式

单时钟方式的特点是电路只有一个CLK信号，且加减仅由U’/D的电平决定。74LS191是利用单时钟方式构成的同步加减计数器。其输入端的逻辑式为：

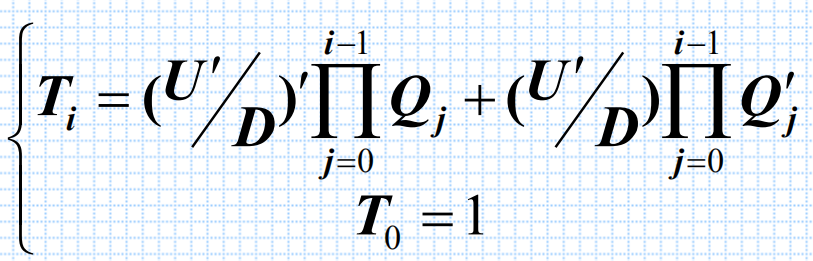
【功能表】

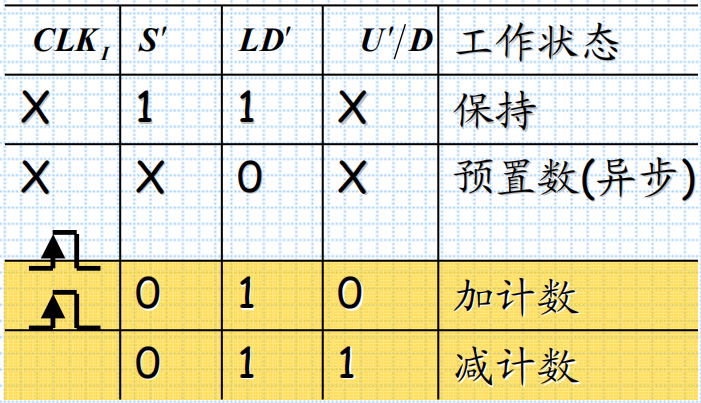
从功能表可以看出，当U’/D = 0时做加法计数，U’/D = 1时做减法计数。LD’ = 0时电路为异步预置数状态，S’为总开关。

 
74LS191为异步预置数，而74161为同步预置数，但两者同为异步置零。
 

（2）双时钟方式

双时钟方式的特点是加法脉冲和减法脉冲来自两个不同的脉冲源。74LS193就是由这种方法构成的加减计数器，74LS193也具有异步置零和异步置数的功能。

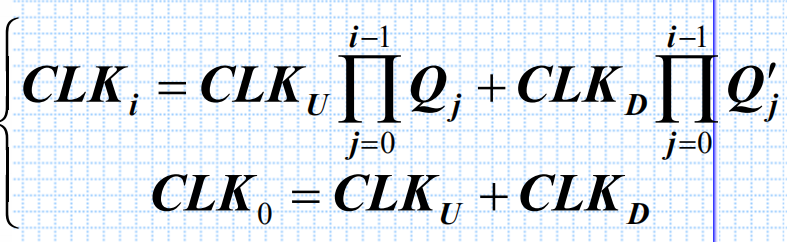
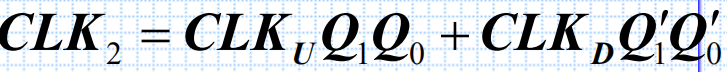
ii. 同步十进制计数器

1. 同步十进制加法计数器 74160

在四位同步二进制计数器的基础上稍加修改，使其计数到1001时即返回0000，这样就制成了同步十进制加法计数器。

【驱动方程】

T0 = 1
T1 = Q0 Q3’
T2 = Q0 Q1
T3 = Q0 Q1 Q2 + Q0 Q3

【状态转换表】

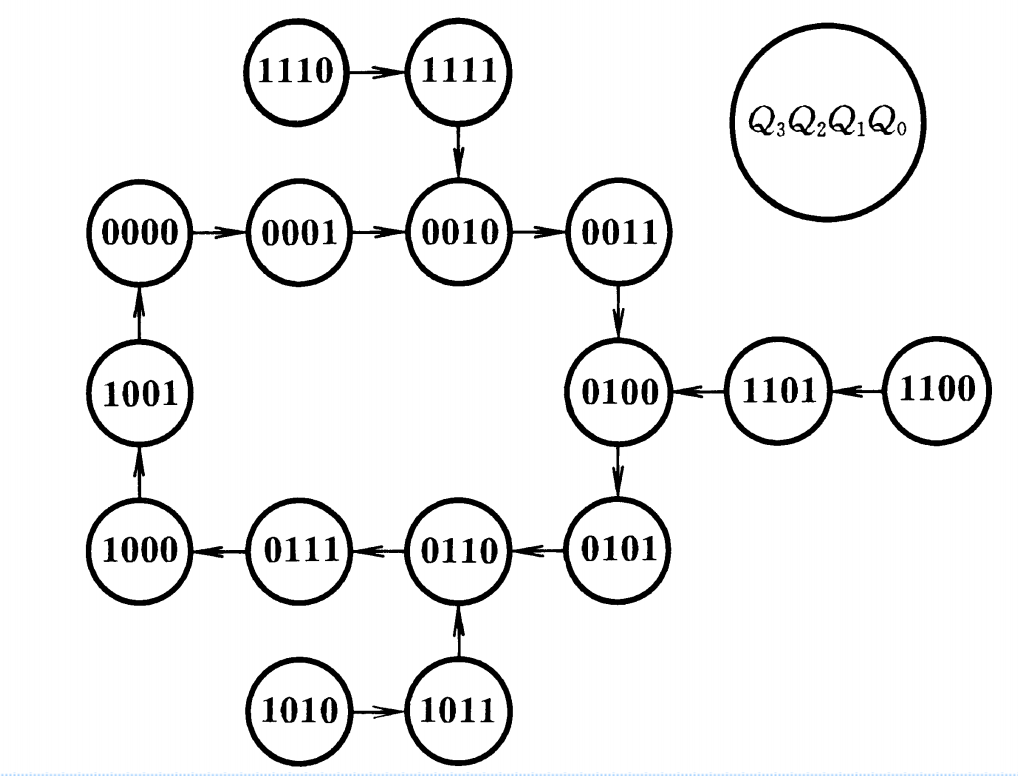
74160在此基础上，又添加了同步预置数、异步置零和保持的功能。

【逻辑框图】

【功能表】

2. 同步十进制减法计数器

T0 = 1
T1 = Q0’ (Q1’ Q2’ Q3’)’
T2 = Q0’ Q1’ (Q1’ Q2’ Q3’)’
T3 = Q0’ Q1’ Q2’

【状态转换图】

II. 异步计数器

1. 异步二进制计数器

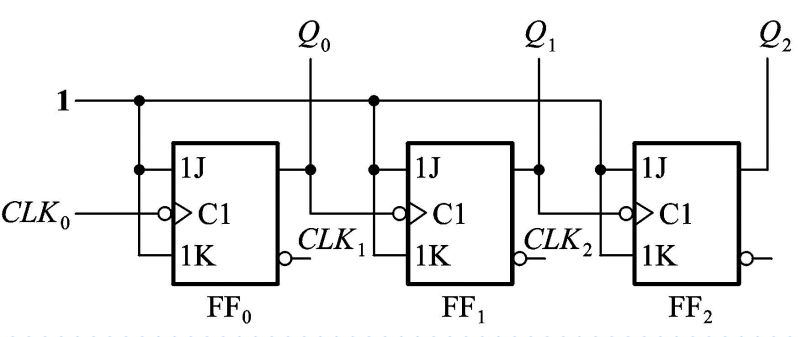
异步计数器中的各个触发器不是同步翻转的，在末位+1时，从低位到高位逐位进行进位。异步二进制加法计数器和异步二进制减法计数器均采用了将低位触发器的一个输出端接入到高位触发器的时钟输入端的方法。

【电路图】

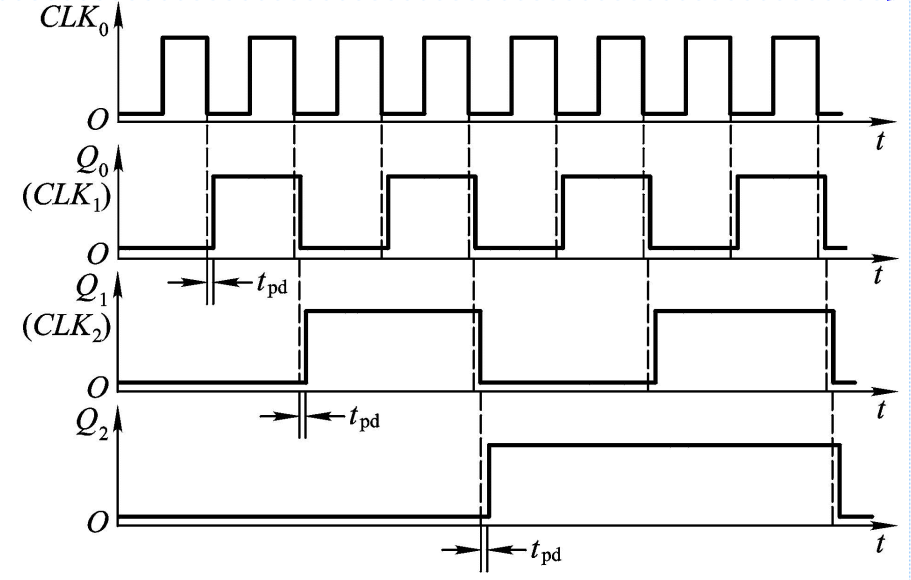
由于触发器的新状态的建立要比CLK下降沿滞后一个传输延迟时间，故其时序波形图如下：

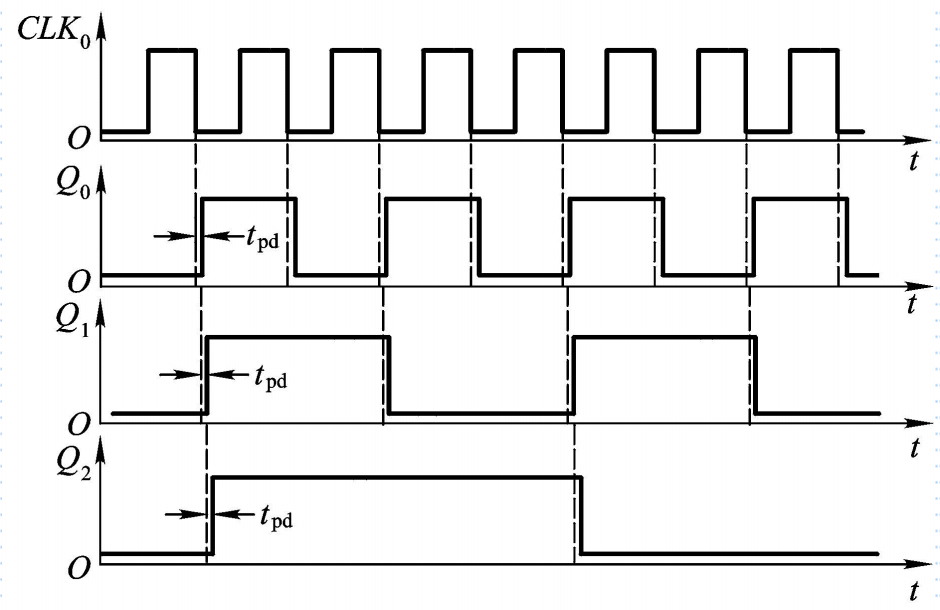
2. 异步十进制计数器 74LS290

异步十进制计数器74LS290便是由4位异步二进制计数器连接而成的。其电路图如下：

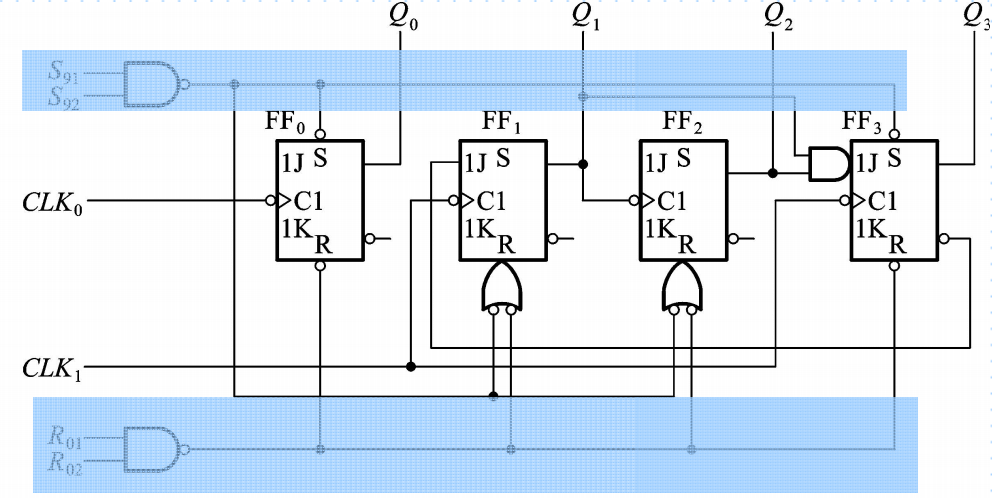
异步计数器与同步计数器相比，结构更为简单，但是异步计数器的工作效率较低，且在译码时会产生竞争-冒险现象。
 

III. 移位寄存器型计数器

1. 环形计数器

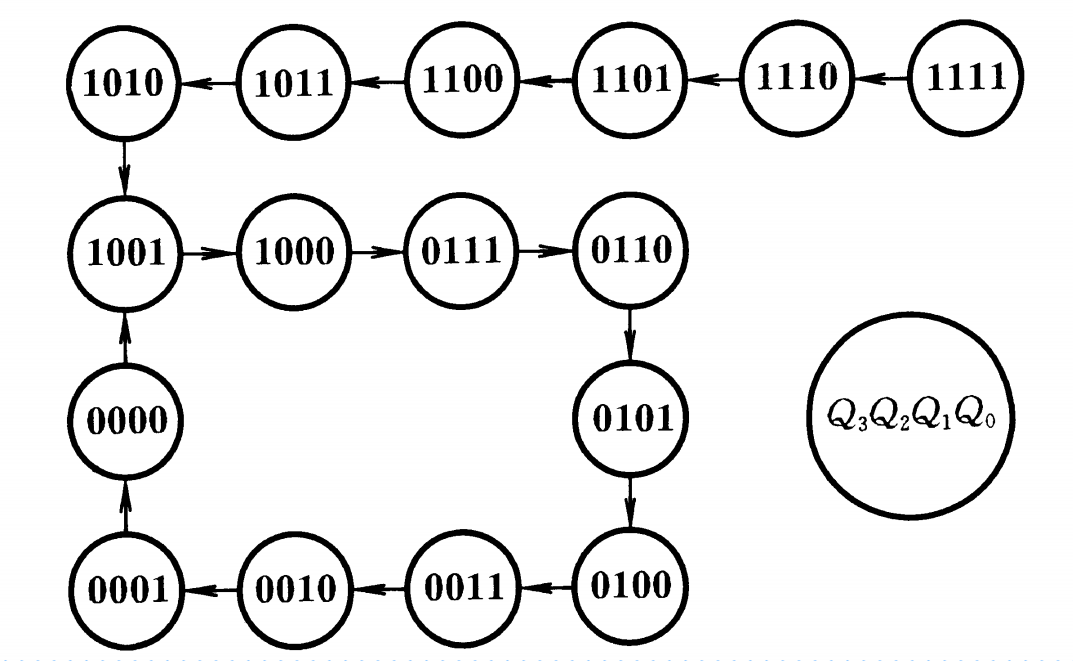
将移位寄存器首尾相接(D0=Q3)即可构成环形计数器，此环形计数器在连续脉冲作用下可以实现数据的循环右移。环形计数器的优点是电路结构极其简单，且不需要译码器，它的缺点是没有充分利用电路的状态。

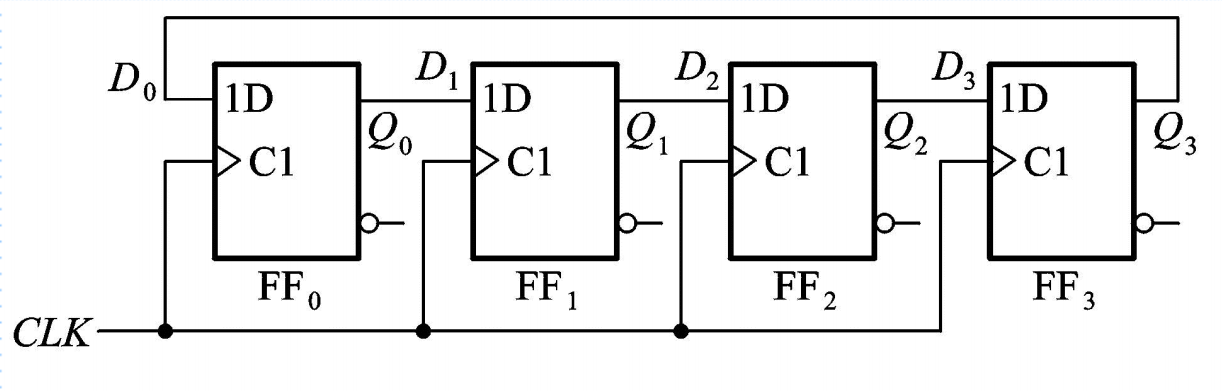
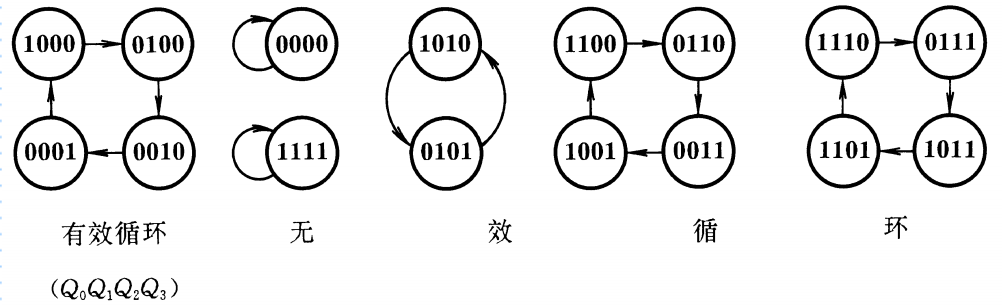
从状态转换图可以看出，普通的环形计数器不能实现自启动，只能取由1000、0100、0010、0001为有效循环，通常我们可以接入适当的反馈逻辑电路让环形计数器能够实现自启动。
 

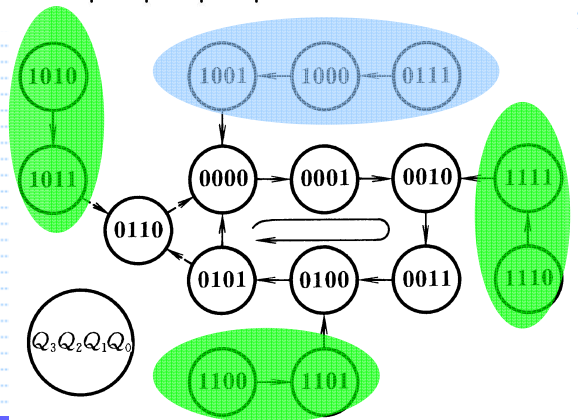
2. 扭环形计数器

我们可以通过改变反馈逻辑电路来增加环形计数器的电路状态利用率。若令D0=Q3’，则此环形计数器被改造成了扭环形计数器。普通扭环形计数器有两个状态循环，其中一个为无效循环，无法自启动。若又令D0 = Q1 Q2’ + Q3’，则该扭环形计数器可以自启动。

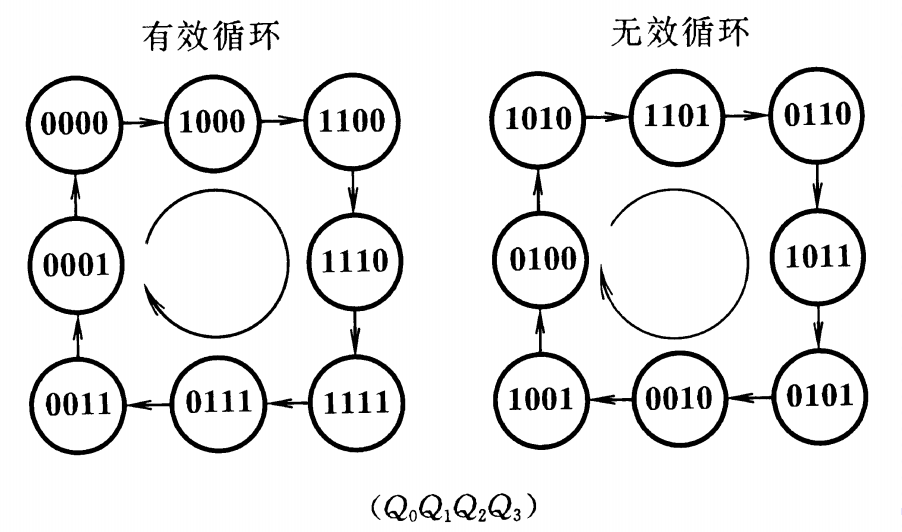
使用n位移位寄存器的扭环形计数器可以得到2n个有效状态的循环，其状态利用率是环形计数器的两倍，且不会产生竞争-冒险现象。
 

IV. 任意进制计数器的构成方法

若已有N进制计数器，需要得到M进制计数器，则此时应分为M<N和M>N这两种情况来讨论。

1. M < N的情况

这种情况下，我们必须设法让M~N中间的状态跳过，才可以得到M进制计数器。实现这种跳跃的方法有置零法和置数法两种。

(1) 置零法

置零法适用于有置零输入端的计时器。置零法不需要考虑D端，对于进位信号的产生，则需要根据实际情况来判断是否需要进位输出端C，若不需要C则进位脉冲由Q端直接输出。

对于异步置零的计数器，当它从全0状态S0开始计数并接收了M个计数脉冲后，电路进入SM状态，将此时的SM状态译码成一个置零信号加到置零输入端即可将计数器返回S0状态，从而得到M进制计数器。电路一进入SM状态即被置成S0状态，所以SM状态出现时间极短，故在稳定的状态中不含有SM状态。稳定的状态为S 0 ~ S M-1。

对于同步置零的计数器，由于必须等下一个时钟信号到达后才可以被置零，所以只需要从S M-1状态译码出同步置零信号即可，S M-1也包含在稳定循环当中。

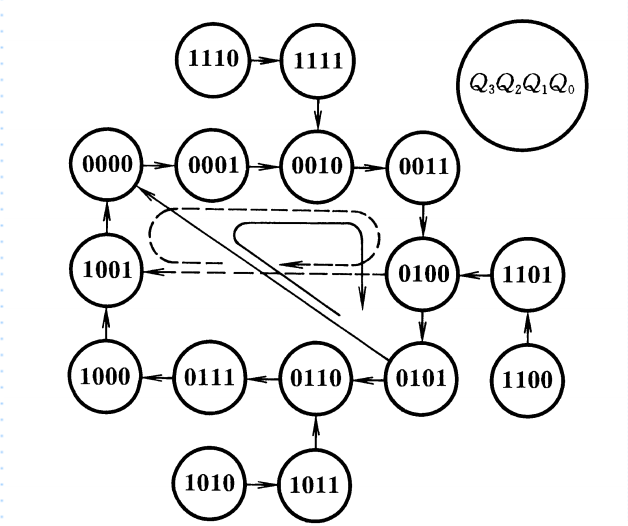
例如，用置零法将异步置零的同步十进制计数器74160接成同步六进制计数器，在状态为0110时立即被置为0000，从而实现0000~0101的六进制循环。为了增加电路可靠性，我们还可以增加一个SR锁存器维持置零信号，用锁存器的Q’端连接RD’端，用Q端连接进位信号输出端。

【状态转换图】

【示意图】

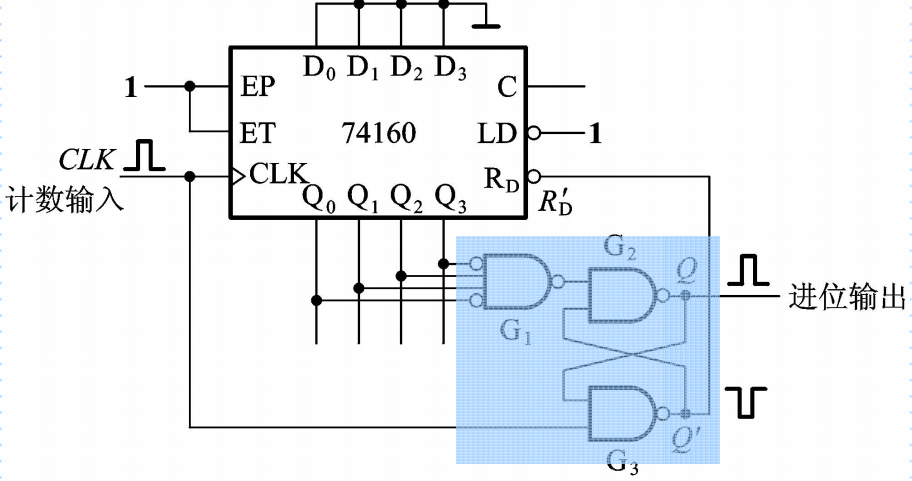
(2) 置数法

置数法也叫置位法，适用于有预置数功能的计数器，它通过给计数器重复置入某个数值的方法来跳跃M~N这些状态，从而获得M进制计数器。

对于异步预置数的计数器，只要LD’=0的信号一出现，则数据会立即置入计数器中，不受CLK信号控制，所以预置数信号应该从S i+1开始译出。S i+1只在很短的时间内存在，不包含在稳定循环中。

对于同步预置数的计数器，预置数信号应该从Si状态开始译出，等到下一个CLK信号到来时才将要置入的数据置入计数器中。

例如，用置数法将同步预置数的同步十进制计数器74160接成同步六进制计数器，从D端置入循环开始状态，从Q端译码输出循环结束状态。

如果预置数为0000，计数循环结束时为0101，则无法从C端产生进位脉冲，故进位脉冲只能从Q2端进位输出。

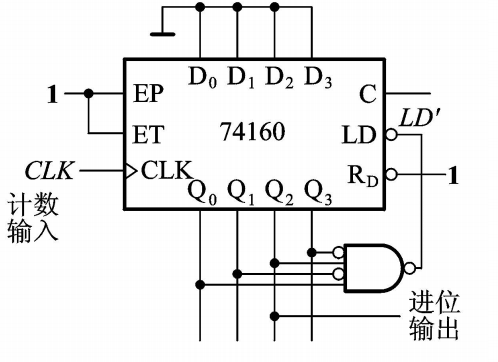
当然，若预置数为1001，则计数循环结束时为0100，此时再返回1001即可产生进位信号，即进位信号从C端输出。

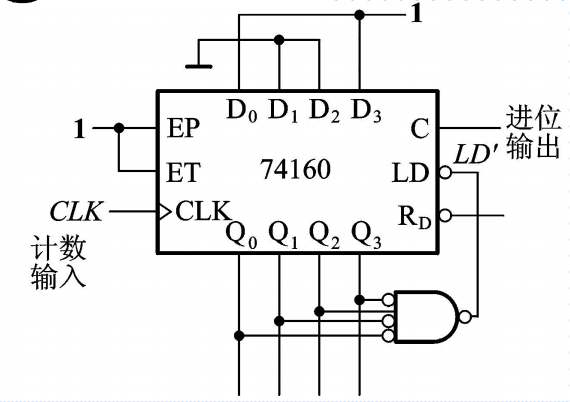
2. M > N的情况

此时则必须用多片N进制计数器组合成M进制计数器。各片之间的连接方式有串行进位方式、并行进位方式、整体置零方式和整体置数方式四种。

(1) 串行进位方式

串行进位方式中以低位片的进位输出信号作为高位片的时钟输入信号。

例如，用串行进位方式将74160接成一百进制计数器：

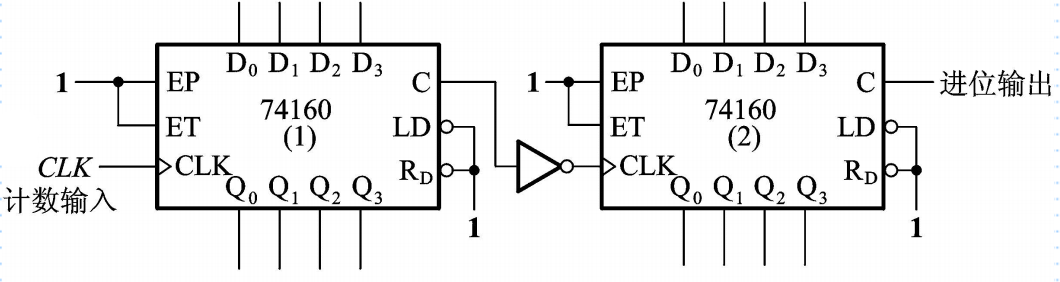
(2) 并行进位方式

并行进位方式中以低位片的进位输出信号作为高位片的工作状态控制信号，且两片的CLK输入端同时接入计数输入信号。

例如，用并行进位方式将74160接成一百进制计数器：

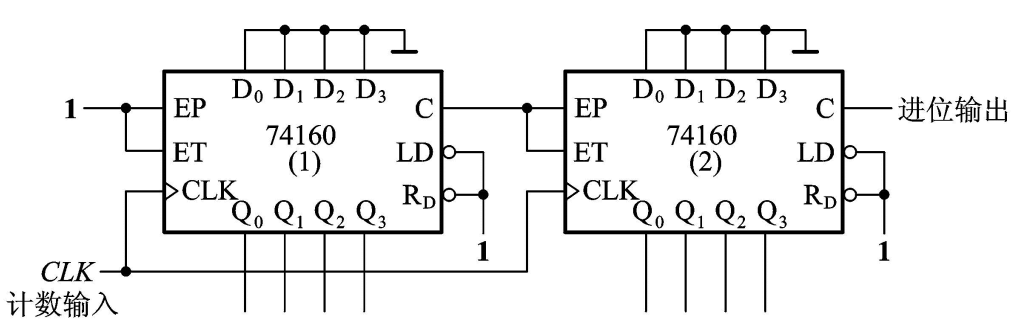
在N1和N2不等于N时，可以先将两个N进制计数器用置零或置数法分别接成N1和N2进制计数器，再用并行或串行进位方式连接起来。

(3) 整体置零方式

当M为素数时，就不能采用串行进位或并行进位的方法了，必须采用整体置零或整体置数的方式。

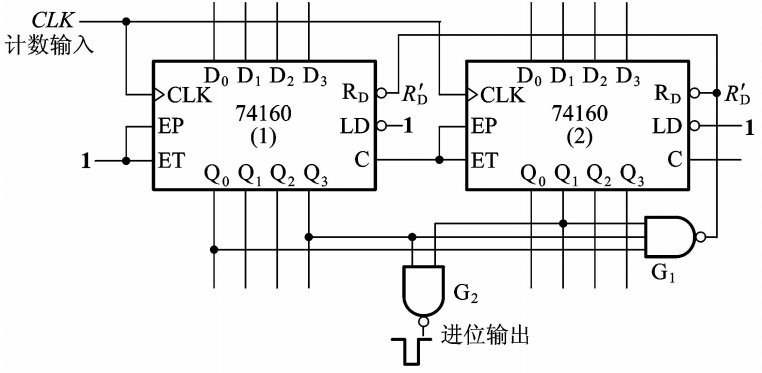
整体置零方式就是先将两片N进制计数器按串行或并行接成一个大于M进制的计数器，再用置零法将相应置零端置零。但整体置零法可靠性差，通常还需要加译码电路才能正常使用。第一片为个位，第二片为十位。整体置零数就是进制数。

例如，用两片同步十进制计数器74160接成一个二十九进制计数器：

29 = 2×10 + 9×1

 

(4) 整体置数方式

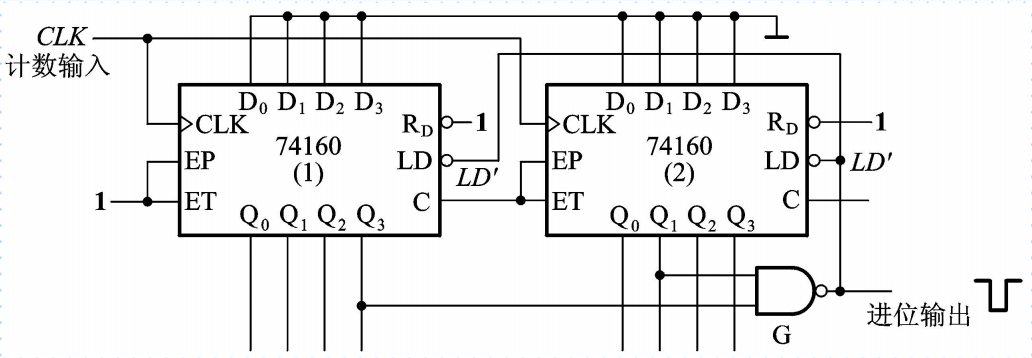
整体置数方式就是先将两片N进制计数器按串行或并行接成一个大于M进制的计数器，再用置数法的原理跳过多余的状态，从而获得M进制计数器。整体置数输出端Q的值要比进制数少一。

例如，用两片同步十进制计数器74160接成一个二十九进制计数器：

29 = 2×10 + 8×1 + 1

最后

以上就是单纯犀牛为你收集整理的【数电】常用时序逻辑电路模块总结同步置零和异步置零同步预置数和异步预置数一. 移位寄存器二. 计数器的全部内容，希望文章能够帮你解决【数电】常用时序逻辑电路模块总结同步置零和异步置零同步预置数和异步预置数一. 移位寄存器二. 计数器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。