第一章 数字与编码
- 前言
- 一、常用数制
- 1、通用格式- -加权和
- 2、一般表达方式- -括号+数字注脚
- 3、码制的英文单词&英文注脚(略)
- 4、思考题
- 二、不同数制间的转换
- 1、其余进制变十进制
- 1)方法一:借加权和
- 2)方法二:利用中间进制- -二进制
- 2、重点: 十进制变二进制
- (1)整数部分:除权取余
- 3、二进制、八进制、十六进制之间的相互转化
- (2)小数部分:乘权取整
- 4、思考题
- 三、二进制的算术运算
- 1、数字电路使用二进制原因之一:
- 2、反码、补码、原码运算
- 3、思考题
- 四、常用编码
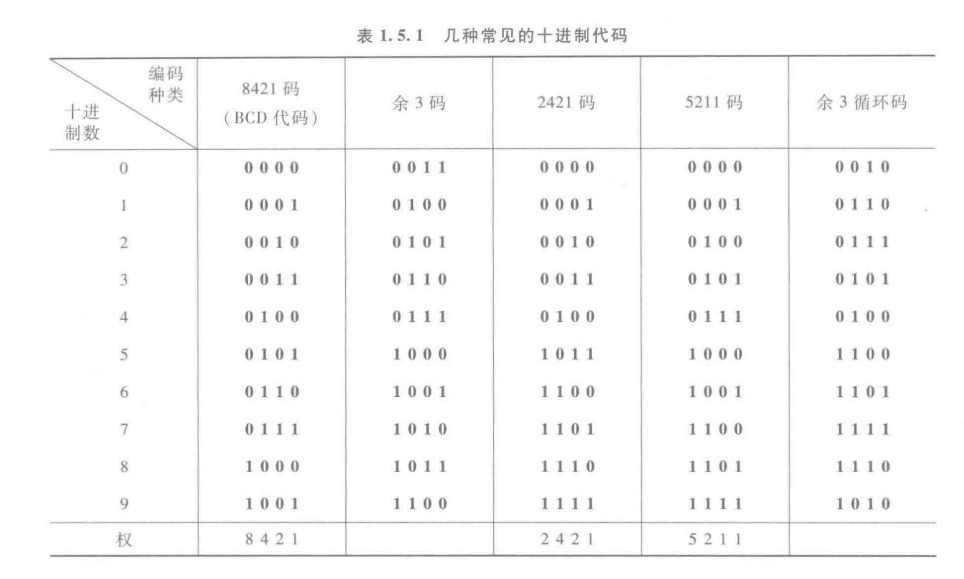
- 1、8421码,即BCD码
- 2、2421码、5211码
- 3、非恒权代码
- 1)命名原因
- 2)余三码
- 3)余三循环码
- 4)格雷码(循环码)
- 4、思考题
前言
阎石 第六版 笔记
一、常用数制
1、通用格式- -加权和
1)其余进制按加权和的形式,可以转为十进制;
2)括号+数字注脚–>加权和展开–>十进制;
3)设整数部分n位,小数部分m位,权值幂的范围:
整数:0–>n-1
小数:-1–>-m

2、一般表达方式- -括号+数字注脚

3、码制的英文单词&英文注脚(略)
4、思考题

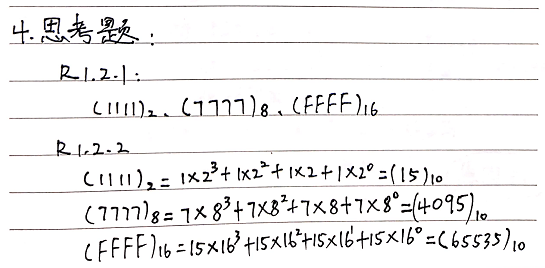
二、不同数制间的转换
1、其余进制变十进制
1)方法一:借加权和
一.2中介绍的:各基数按加权和的形式展开即可,
2)方法二:利用中间进制- -二进制
详见二.3
2、重点: 十进制变二进制

(1)整数部分:除权取余
低位在上,高位在下;
[原因]:
3、二进制、八进制、十六进制之间的相互转化
1)利用4位二进制数=1位十六进制数=2位八进制数的规则;
2)利用中间进制- -二进制;
(8421)
(2)小数部分:乘权取整
[原因]
4、思考题

略
三、二进制的算术运算
1、数字电路使用二进制原因之一:
二进制的+、-、*、%运算,本质上可以转变为“移位”、“相加”两种操作,可以简化电路结构;
2、反码、补码、原码运算

3、思考题

(1)略
(3)略
(2)?
四、常用编码
1、8421码,即BCD码
1)必备:BCD(Binary Coded Decimal);
2)每个二值代码中的每个1都代表一个固定权值,从左到右,每个1分别代表的固定权值为8、4、2、1,恒权代码;
2、2421码、5211码
1)意义与8421码一致;
2)2421码特点:0、9;1、8;2、7;3、6;4、5互为反码。便于求取对10的补码;
3)5211码特点:每一位权正好与8421码十进制计数器的4个触发器输出分频比相对应,对于构成某些数字系统很有用;
3、非恒权代码
1)命名原因
如果为了使非恒权代码的一组二进制数,与其等效是十进制数所表示的一组二进制数相等,则该组非恒权代码的这组二进制数,权值不可以是恒定的;l

2)余三码
[1]算法:相应的8421码基础上加3(即0011);
[2]特点:0、9;1、8;2、7;3、6;4、5互为反码,这对于求取对10的补码是很方便的;
3)余三循环码
[1]算法:在对于的余三码的基础上,从右自左,每两组数进行异或运算。三次异或后,第四位数取余三码首位数字保留;
eg:
| 十进制 | 8421 | 余三码 | 余三循环码 |
|---|---|---|---|
| 2 | 0010 | 0101 | 0111 |
| 3 | 0011 | 0110 | 0101 |
[2]特点:相邻两位代码之间,仅有一位不相同,这对于求取对10的补码是很方便的;
[3]优点:在编码顺序依次转换过程中,由于相邻两位代码,仅有一位不相同,不会产生过度噪声
4)格雷码(循环码)

4、思考题

最后
以上就是寂寞花生最近收集整理的关于数字电子技术基础笔记【阎石第六版】 第一章 数字与编码前言一、常用数制二、不同数制间的转换三、二进制的算术运算四、常用编码的全部内容,更多相关数字电子技术基础笔记【阎石第六版】内容请搜索靠谱客的其他文章。










发表评论 取消回复