一. 解析解方法
正常的求解微分方程的MATLAB格式如下:
y=dsolve(f1,f2,...,fm)如果需要指明自变量,则如下:
y=dsolve(f1,f2,...,fm,'x')格式中的fi既可以描述微分方程,又可以描述初始条件或边界条件。
- 描述微分方程
的MATLAB格式为:D4y=7;
- 描述条件
的MATLAB格式为:D2y(2)=3;
例题1
输入信号u(t)如下:
求解如下微分方程的通解
解:
此题需要分两步解决。
第一步MATLAB代码如下:
clc;clear;
syms t;
u=exp(-5*t)*cos(2*t+1)+5;
uu=5*diff(u,t,2)+4*diff(u,t)+2*u %等式右边运行结果:
uu =87*exp(-5*t)*cos(2*t + 1) + 92*exp(-5*t)*sin(2*t + 1) + 10
第二步MATLAB代码如下:
clc;clear;
syms t y;
y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=87*exp(-5*t)*cos(2*t+1)+92*exp(-5*t)*sin(2*t+1)+10'],...
'y(0)=3','Dy(0)=2','D2y(0)=0','D3y(0)=0')
运行结果如下:
y =(exp(-5*t)*(37960*exp(2*t) - 53820*exp(3*t) + 29640*exp(4*t) + 650*exp(5*t) - 1029*cos(2*t + 1) - 1641*sin(2*t + 1) - 9750*exp(t) + 975*exp(2*t)*sin(1) - 6120*exp(3*t)*sin(1) + 2522*exp(4*t)*sin(1) - 14092*cos(1)*exp(t) + 4264*exp(t)*sin(1) + 34905*cos(1)*exp(2*t) - 26700*cos(1)*exp(3*t) + 6916*cos(1)*exp(4*t)))/1560
例题2
求解如下微分方程组
解:
MATLAB代码如下:
clc;clear;
[x,y]=dsolve('D2x+2*Dx=x+2*y-exp(-t)','Dy=4*x+3*y+4*exp(-t)')运行结果:
x =exp(t*(6^(1/2) + 1))*(6^(1/2)/5 - 1/5)*(C2 + exp(- 2*t - 6^(1/2)*t)*((11*6^(1/2))/3 - 37/4)) - exp(-t)*(C1 + 6*t) - exp(-t*(6^(1/2) - 1))*(6^(1/2)/5 + 1/5)*(C3 - exp(6^(1/2)*t - 2*t)*((11*6^(1/2))/3 + 37/4))
y = exp(-t)*(C1 + 6*t) + exp(t*(6^(1/2) + 1))*((2*6^(1/2))/5 + 8/5)*(C2 + exp(- 2*t - 6^(1/2)*t)*((11*6^(1/2))/3 - 37/4)) - exp(-t*(6^(1/2) - 1))*((2*6^(1/2))/5 - 8/5)*(C3 - exp(6^(1/2)*t - 2*t)*((11*6^(1/2))/3 + 37/4))
写成数学形式:
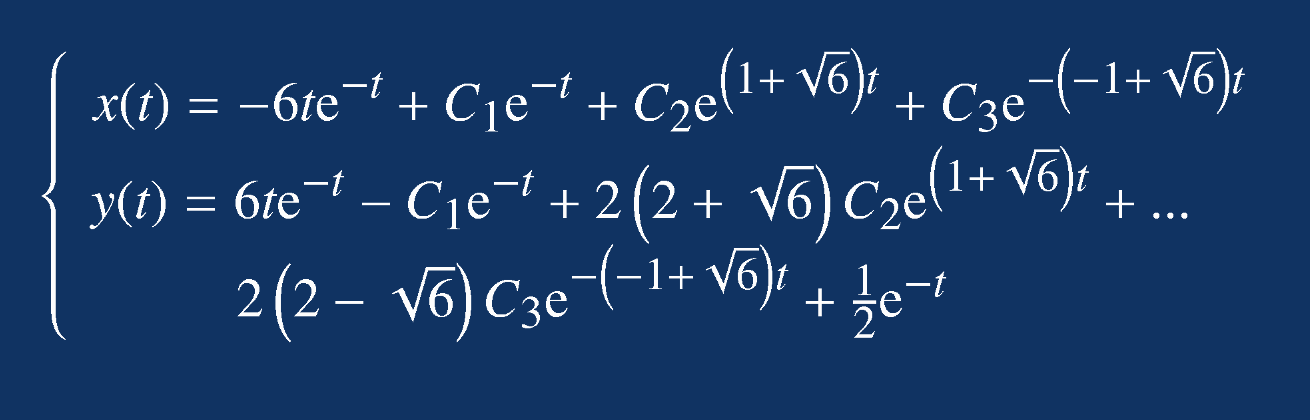
例题3
求解以下微分方程的解析解。
(1)
(2)
解:
MATLAB代码如下:
clc;clear;
syms t x X;
%第一题
x=dsolve('Dx=x*(1-x^2)')
%第二题
X=dsolve('DX=X*(1-X^2)+1')
%实际上第二题没有解析解
%只有部分非线性方程有解析解
第一题运行结果:
x =
0
1
-1
(-1/(exp(C1 - 2*t) - 1))^(1/2)
第二题运行结果:
警告: Unable to find explicit solution. Returning implicit solution instead.
X =
root(z^3 - z - 1, z, 1)
root(z^3 - z - 1, z, 2)
root(z^3 - z - 1, z, 3)
二. 微分方程的算法分析
微分方程的通式如下:
上式子中为状态向量,
可以是任意非线性函数。
以下以Euler算法为例子,进行分析。
2.1 数学分析
时刻系统状态向量表示为如下:
微分方程左侧的导数可近似表示为如下:
时刻微分方程的近似解可表示为如下:
在时刻系统的状态向量可表示为如下:
在时刻系统的状态向量表示为如下:
所以,在时Euler算法的数值解为如下:
图像形式表示为如下:
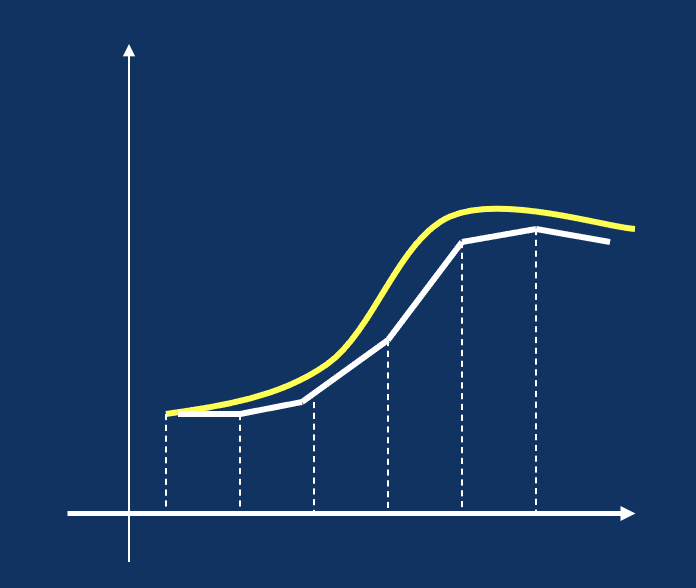
理论上讲,h越小,微分效果越好。但是不能无限制地减小h的值,其中有两个原因:
- 减慢计算速度
- 增加累积误差
在对微分方程求解过程中,有以下三个技巧:
- 选择适当的步长
- 改进近似算法精度
- 采用变步长方法
2.2代码分析
构建函数代码算法如下:
function [outx,outy]=MyEuler(fun,x0,xt,y0,PointNum)
%fun表示f(x,y)
%x0,xt代表自变量的初值和终值
%y0:函数在x0处的值,也可以是向量的形式
%PointNum 代表自变量在[x0,xt]上取的点数
if nargin<5|PointNum<=0
PointNum=100; %PointNum默认值为100
end
if nargin<4
y0=0; %y0默认值为0
end
h=(xt-x0)/PointNum; %计算步长h
x=x0+[0:PointNum]'*h; %自变量数组
y(1,:)=y0(:)'; %将输出存为行向量,输出为列向量形式
for k=1:PointNum
f=feval(fun,x(k),y(k,:));
f=f(:)'; %计算f(x,y)在每个迭代点的值
y(k+1,:)=y(k,:)+h*f; %对于所取的点x,迭代计算y值
end
outy=y;
outx=x;
plot(x,y) %画出方程解的函数图例题4
求以下微分方程组的h=0.2和h=0.4的数值解。
解:
此MATLAB文件分成三个部分:
(1)欧拉算法文件
function [outx,outy]=MyEuler(fun,x0,xt,y0,PointNum)
%fun表示f(x,y)
%x0,xt代表自变量的初值和终值
%y0:函数在x0处的值,也可以是向量的形式
%PointNum 代表自变量在[x0,xt]上取的点数
if nargin<5|PointNum<=0
PointNum=100; %PointNum默认值为100
end
if nargin<4
y0=0; %y0默认值为0
end
h=(xt-x0)/PointNum; %计算步长h
x=x0+[0:PointNum]'*h; %自变量数组
y(1,:)=y0(:)'; %将输出存为行向量,输出为列向量形式
for k=1:PointNum
f=feval(fun,x(k),y(k,:));
f=f(:)'; %计算f(x,y)在每个迭代点的值
y(k+1,:)=y(k,:)+h*f; %对于所取的点x,迭代计算y值
end
outy=y;
outx=x;
plot(x,y) %画出方程解的函数图文件命名:MyEuler.m
(2)函数文件
function f=myfun01(x,y)
f=sin(x)+y;文件命名:myfun01.m
(3)主运行文件
clc;clear;
[x1,y1]=MyEuler('myfun01',0,2*pi,1,16); %欧拉法所得的解
h1=2*pi/16 %计算取16的步长
[x11,y11]=MyEuler('myfun01',0,2*pi,1,32); %欧拉法所得的解
h2=2*pi/32 %计算取32点的步长
y=dsolve('Dy=y+sin(t)','y(0)=1');
for k=1:33
t(k)=x11(k);
y2(k)=subs(y,t(k)); %求其对应点的离散解
end
plot(x1,y1,'+b',x11,y11,'og',x11,y2,'*r')
legend('h=0.4的欧拉法解','h=0.2的欧拉法解','符号解');运行结果:
h1 =0.392699081698724
h2 =0.196349540849362
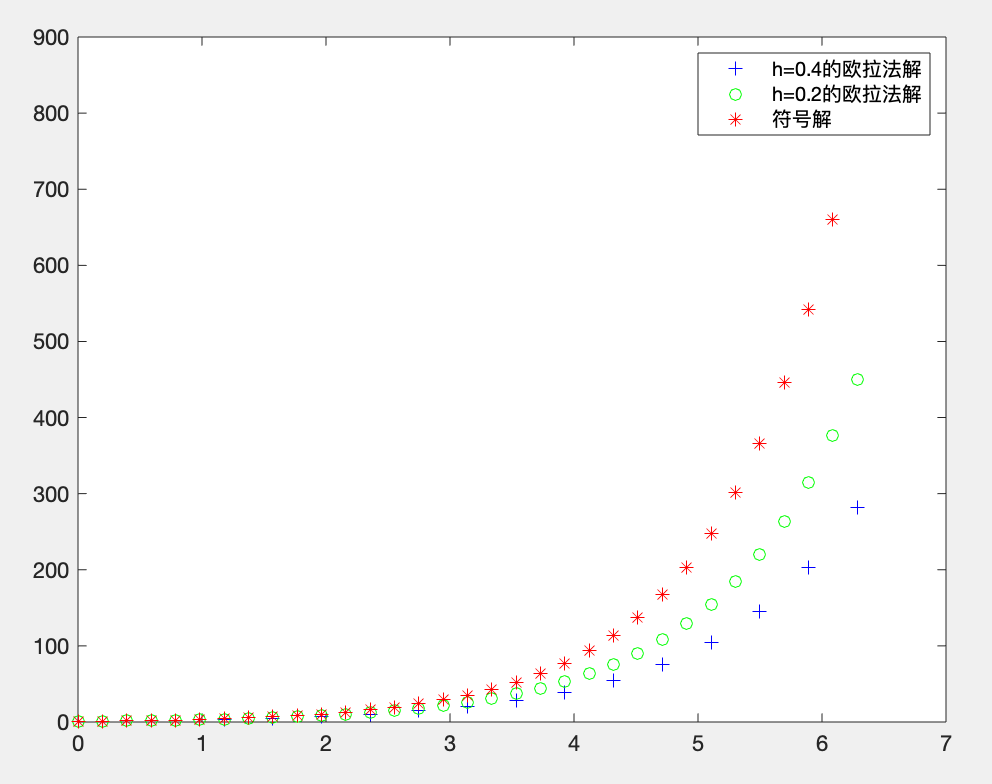
观察图像可以发现,此Euler方法和解析法相比,精准度还有一定的距离。于是提出以下改进版的欧拉方法
此时此题将有四个文件:
(1)原函数文件
function f=myfun01(x,y)
f=sin(x)+y;(2)欧拉算法文件
function [outx,outy]=MyEuler(fun,x0,xt,y0,PointNum)
%fun表示f(x,y)
%x0,xt代表自变量的初值和终值
%y0:函数在x0处的值,也可以是向量的形式
%PointNum 代表自变量在[x0,xt]上取的点数
if nargin<5|PointNum<=0
PointNum=100; %PointNum默认值为100
end
if nargin<4
y0=0; %y0默认值为0
end
h=(xt-x0)/PointNum; %计算步长h
x=x0+[0:PointNum]'*h; %自变量数组
y(1,:)=y0(:)'; %将输出存为行向量,输出为列向量形式
for k=1:PointNum
f=feval(fun,x(k),y(k,:));
f=f(:)'; %计算f(x,y)在每个迭代点的值
y(k+1,:)=y(k,:)+h*f; %对于所取的点x,迭代计算y值
end
outy=y;
outx=x;
plot(x,y) %画出方程解的函数图(3)改进版欧拉算法文件
function [Xout,Yout]=MyEulerPro(fun,x0,xt,y0,PointNumber)
%用改进的欧拉法解微分方程
if nargin<5|PointNumber<=0 %PointNumber默认值为100
PointNumber=100;
end
if nargin<4 %y0默认值为0
y0=0;
end
h=(xt-x0)/PointNumber; %计算所取的两离散点之间的距离
x=x0+[0:PointNumber]'*h; %表示出离散的自变量x
y(1,:)=y0(:)';
for i=1:PointNumber %迭代计算过程
f1=h*feval(fun,x(i),y(i,:));
f1=f1(:)';
f2=h*feval(fun,x(i+1),y(i,:)+f1);
f2=f2(:)';
y(i+1,:)=y(i,:)+1/2*(f1+f2);
end
Xout=x;
Yout=y;(4)主运行文件
clc;clear;
%此处对比改进版欧拉法,简单欧拉法以及微分方程的符号解
[x3,y3]=MyEulerPro('myfun01',0,2*pi,1,128);
[x,y1]=MyEuler('myfun01',0,2*pi,1,128);%欧拉法所得的解
y=dsolve('Dy=y+sin(t)','y(0)=1'); %该微分方程的符号解
for k=1:129 %点数
t(k)=x(k); %代入
y2(k)=subs(y,t(k)); %求其对应点的离散解,也就是计算y
end
plot(x,y1,'-b',x3,y3,'og',x,y2,'*r')
legend('简单欧拉法解','改进欧拉法解','符号解');运行结果:
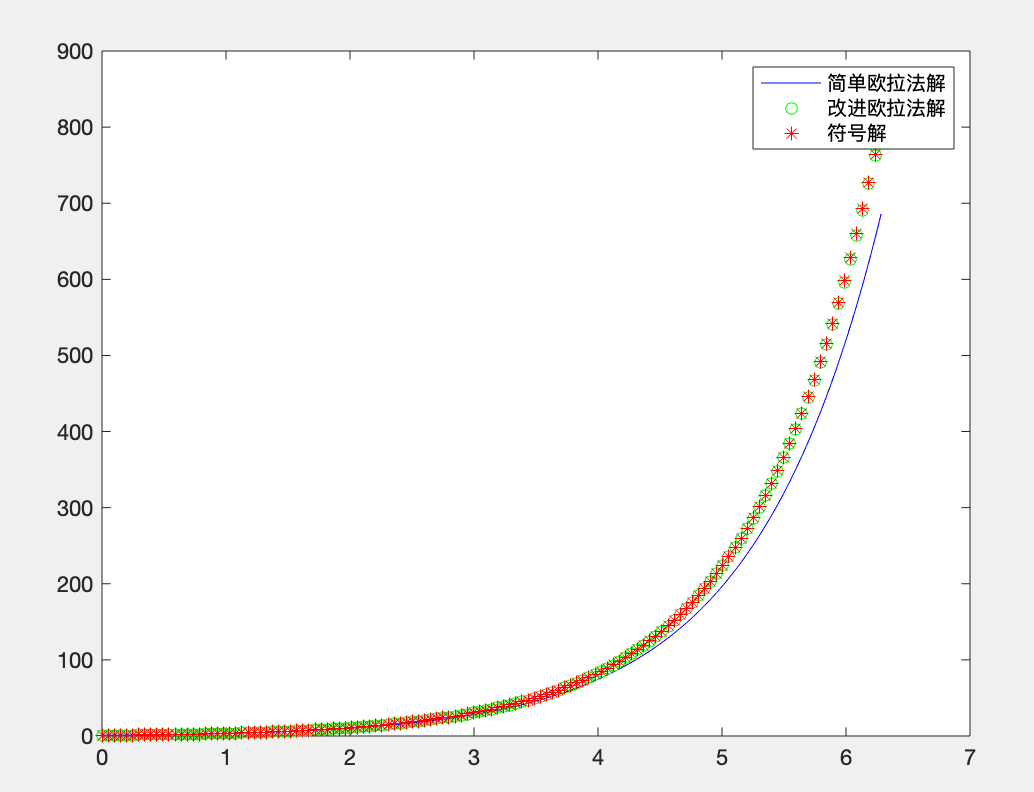
最后
以上就是健壮野狼最近收集整理的关于基于MATLAB的微分方程的解析解与欧拉算法的数值解(附完整代码)一. 解析解方法二. 微分方程的算法分析的全部内容,更多相关基于MATLAB的微分方程的解析解与欧拉算法的数值解(附完整代码)一.内容请搜索靠谱客的其他文章。








发表评论 取消回复