微分方程概述及matlab代码（求解析解）

【清风数学建模教程笔记】

微分方程概述

当我们描述实际对象的某些特性随时间（空间）而演变的过程，分析它的变化规律，预测它的未来形态、研究它的控制手段时。通常要建立对象的动态模型。

在许多实际问题中，当直接导出变量之间的函数关系较为困难，但导出包含未知函数的导数或微分的关系式比较容易时，可以用建立微分方程模型的方法来研究该问题。

1. 分类：常微分方程（未知函数是一个一元函数）和偏微分方程（未知函数是一个多元函数）
2. 国赛趋势：越来越重视微分方程、物理领域等
3. 解析解和数值解
   • 解析解(analytical solution)是严格按照公式逻辑推导得到的，具有基本的函数形式。给出任意的自变量就可以求出其因变量，也就是问题的解，他人可以利用这些公式计算各自的问题，具有广泛适用性；
   • 数值解(numerical solution)是采用某种计算方法，在特定的条件下得到的一个近似数值结果，如有限元法，数值逼近法，插值法等等得到的解。别人只能利用数值计算的结果，而不能随意给出自变量并求出计算值。
4. 微分方程模型的应用十分广泛：例如人口预测模型、捕食者猎物模型、种群相互竞争依存模型、传染病模型等

关于传染病模型的学习资源

1. 上海财经大学传染病模型讲解
2. 上海市现代应用数学重点实验室对新冠肺炎的一些研究报告(emo 看不懂)

引例：导弹射击问题

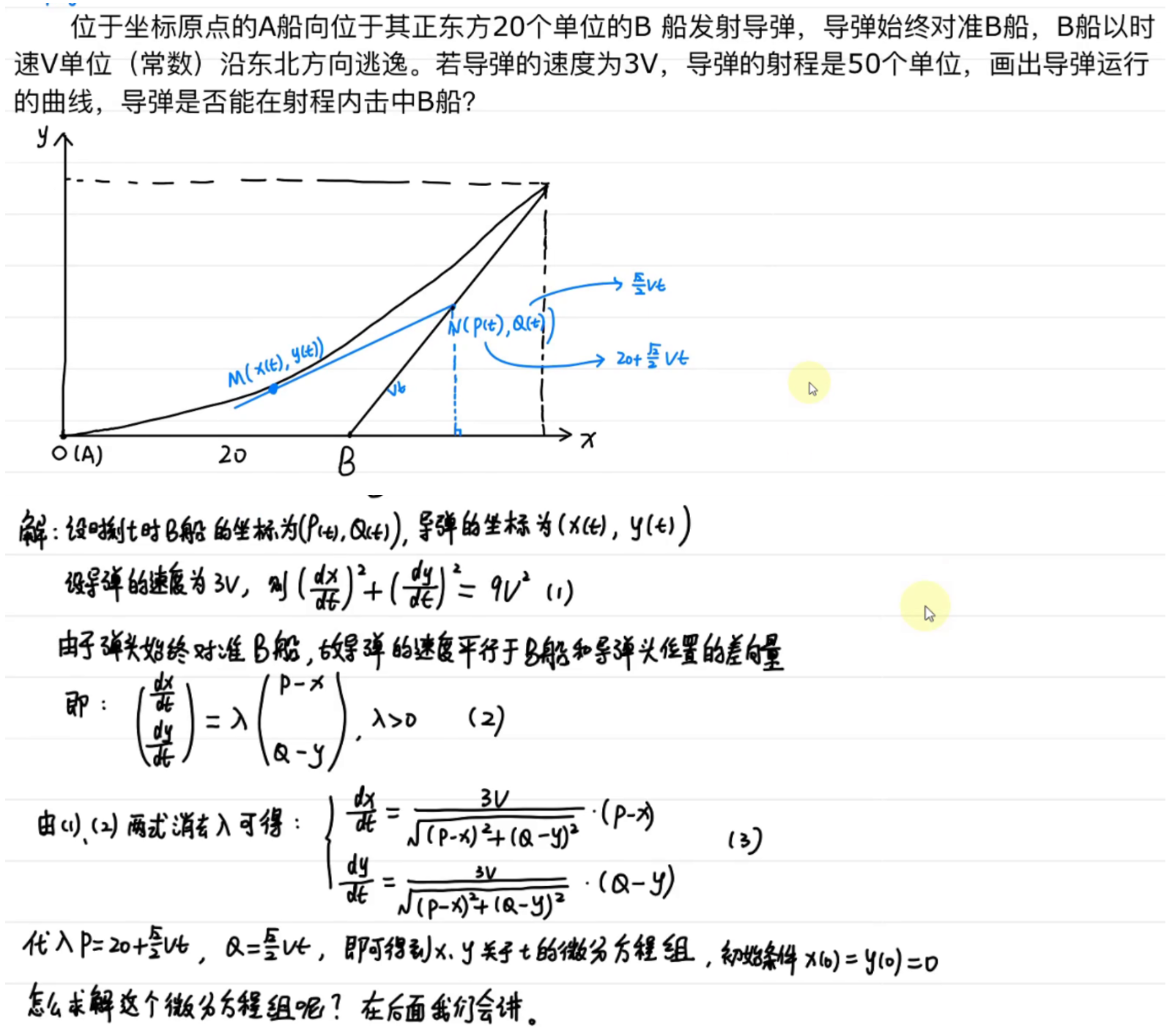
微分方程基本概念

1. 微分方程：含导数或微分的方程称为微分方程，其一般形式为
   $$f(x,y^1,y^2,...,y^n)=0$$

2. 微分方程的阶数：微分方程中所含导数或微分的最高阶数称为微分方程的阶数，例如下式是三阶微分方程。
   $$y^{\prime \prime \prime }+2y^{\prime \prime }-2x=0$$

3. 微分方程的解：使得微分方程成立的函数称为微分方程的解。

4. 微分方程的通解和特解：不含任意常数的解称为微分方程的特解；若解中所含的相互独立的任意常数的个数与微分方程的阶数相等，则称此解为微分方程的通解。例如：
   $$y^{\prime }-e^x=0$$
   特解为
   $$e^x$$
   通解为
   $$e^x+C$$

5. 初值条件：能够确定通解中任意常数的条件称为微分方程的初值条件。

6. 如何建立微分方程？

   • 按照专业知识、规律直接列方程。
   • 套用现有的微分方程模型。（根据具体问题改进）

Matlab求微分方程的解析解

解析解：即给出解的具体表达式，若给定初始条件，则能求出含具体常数的解。

以下给出几个例子。

例1：
$$y-\frac{dy}{dx}=2x$$

clear;clc
dsolve('y-Dy=2*x','x')  
%此处要指定自变量为x
% 输出 2*x + C1*exp(x) + 2  (这里的C1表示任意常数，有时候也会出现C2 C3等)
% 如果不指定自变量的话，会默认自变量为t，x会看成一个常数

% 下面这种写法是新版的matlab推荐的方式,注意：最新版本的matlab会逐渐淘汰上面那种写法
syms y(x)
eqn = (y - diff(y,x) == 2*x);    % 注意原来方程中的“=”一定要改成“==”
dsolve(eqn)

当微分方程中还有其他的未知参数时
$$y-\frac{dy}{dx}=ax$$

% 方法1
dsolve('y-Dy=a*x','x')  % a是一个未知的参数
% 方法2
syms y(x) a
eqn = (y - diff(y,x) == a*x);  
dsolve(eqn)

例2：
$$y-y^{\prime }=2x且y(0)=3$$

% 方法1
dsolve('y-Dy=2*x','y(0)=3','x')
% 输出：2*x + exp(x) + 2
% 方法2
syms y(x)
eqn = (y - diff(y,x) == 2*x);  
%初值条件
cond = (y(0) == 3);
dsolve(eqn,cond)
% 2*x + exp(x) + 2

例3：
$$y^{\prime \prime }+4y^{\prime }+29y=0且y(0)=0,y^{\prime }(0)=15$$

% 方法1
dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x') 
% 3*sin(5*x)*exp(-2*x)
% 方法2
syms y(x)
eqn = (diff(y,x,2) + 4 *diff(y,x) + 29*y  == 0);  
Dy = diff(y,x); % 定义变量Dy为y的一阶导数
cond = [(y(0) == 0) ,(Dy(0) ==15)] ; 
% 有两个条件，可以写到一个向量中保存
dsolve(eqn,cond)
% 3*sin(5*x)*exp(-2*x)

例4：

微分方程组求解，具体见以下代码。

% 方法1
[x,y,z] = dsolve('Dx=2*x-3*y+3*z+t','Dy=4*x-5*y+3*z+t','Dz=4*x-4*y+2*z+t','t') 

% 方法2
syms x(t) y(t) z(t)
eqn1 = (diff(x,t)  == 2*x-3*y+3*z+t); 
eqn2 = (diff(y,t)  == 4*x-5*y+3*z+t); 
eqn3 = (diff(z,t)  == 4*x-4*y+2*z+t); 
eqns = [eqn1 eqn2 eqn3];
[x,y,z] = dsolve(eqns)
% x = exp(2*t)*(C2- (exp(-2*t)*(2*t + 1))/4) + C3*exp(-t)
% y = exp(2*t)*(C2 - (exp(-2*t)*(2*t + 1))/4) + C3*exp(-t) + C4*exp(-2*t)
% z = exp(2*t)*(C2 - (exp(-2*t)*(2*t + 1))/4) + C4*exp(-2*t)

关于mupad工具包以及不手打公式的工具等

mupad  % 最新版本matlab可能会报错，将计算结果复制到里面，使结果可读。
% 如果新版matlab用不了mupad的话，可以使用实时脚本（【新建】-【实时脚本】）
simplify(y)  % simplify函数可以简化表达式
latex(y) 
% 转换成latex代码，复制到Axmath或者word自带的公式编辑器
% 如果太过于复杂的话可能会报错，可以自己测试

关于导弹射击问题的matlab求解

% 假设 v=100
[x,y] = dsolve('Dx = 3*100*(20+sqrt(2)/2*100*t-x)/sqrt((20+sqrt(2)/2*100*t-x)^2+(sqrt(2)/2*100*t-y)^2)','Dy = 3*100*(sqrt(2)/2*100*t-y)/sqrt((20+sqrt(2)/2*100*t-x)^2+(sqrt(2)/2*100*t-y)^2)','x(0)=0,y(0)=0','t')  
% 警告: Explicit solution could not be found. 不能找到显示解

此题无法使用求解析解的方法求解。

关于Matlab求解析解的几点注意

1. 自变量需要指定，当不指定时默认为t
2. 初始条件不给时，算出来的是通解
3. 可以用向量的方式保存微分方程组并求解
4. 如果微分方程形式较为复杂，那么很大可能是得不到解析解的，则需要求数值解

最后

以上就是孤独冰棍为你收集整理的微分方程概述及matlab代码（求解析解）微分方程概述及matlab代码（求解析解）的全部内容，希望文章能够帮你解决微分方程概述及matlab代码（求解析解）微分方程概述及matlab代码（求解析解）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。