最近使用RNN网络解决优化问题时需要解常微分方程,最开始使用matlab包ode45解,发现在某个数据集中出现ode45跑不出结果的情况(不报错)经过搜索发现,ode45只能用来解决非刚性的常微分方程,于是换用ode15s解。problem solved!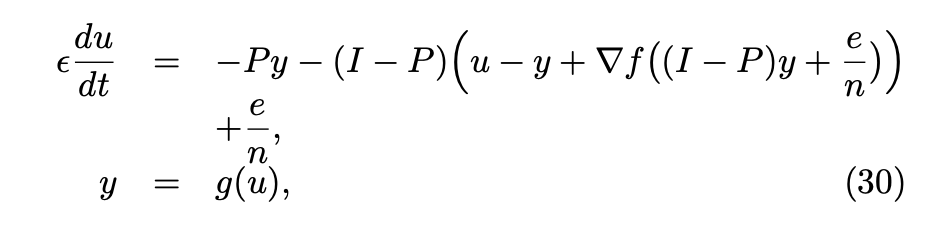
程序:(常微分方程定义)
%定义常微分方程
function dudt = odepseudoGSM(t, u, f, P, q, I, miu, gaa, rf, wk_return_d1_train, weeks, ep)%ep是epsilon
%syms x;
[M, N] = size(wk_return_d1_train);
x=max(0,u);%relu(u)
g = (I - P) * x + q;%
%fprintf('good g %fn',g);%465个,48个的和为1,全为正数
%dfx=(2*V*g*(g'*miu)-g'*V*g*miu)'/(g'*miu).^2; %df(x) change ~~~
rb = rf(weeks);
dDSR1 = zeros(M, N);
for dd=1:N %days即论文中的m天, dd是第j天
rj = wk_return_d1_train(:,dd);%rj是1列
if rj'*g >= rb
dDSR1(:,dd) = zeros(M,1);
%dDSR1(dd)=dDSR_dd;%第j天的DSR分量的导数
elseif rj'*g < rb
dDSR1_dd = 2 * rj * (rj' * g - rb);%% 是个向量不是数字 无法直接求和 %第j天的DSR分量的导数%把1改成了rb
dDSR1(:,dd) = dDSR1_dd;
%dDSR1(dd)
end
end
%对dDSR的所有行求和,dDSR是个列向量
dDSR = sum(dDSR1, 2) / N;%DSR(x)的导数
dfx = 0.5 * gaa^2 * dDSR - gaa * miu;
dudt = 1 / ep * [-P * x - (I - P) * (u - x + dfx) + q]; %equation (16)
end解常微分方程:
function xk = NNN_IG_536(weeks, wk_return_d1, rf, miu) %weeks是周数,wk_return_d1是全部数据,rb是全部数据,miu是training的均值
wk_return_train = wk_return_d1(:, 1:weeks); %online
[M, ~] = size(wk_return_train);
P = 1 / M * ones(M, M);
I = eye(M);
q = 1 / M * ones(M, 1);
%初始化迭代
x0 = 1 / M * ones(M, 1); %用equally weighted初始化
iter = 17;
ga = zeros(iter, 1); %列向量记录gamma迭代结果
DSR0 = DSR_a(weeks, wk_return_d1, x0, rf); %初始化DSR0
ga(1) = (miu' * x0 - rf(weeks)) / DSR0; %初始化的gamma值
gaa = ga(1);
dsr_p = zeros(iter, 1);
iteration = 1;
while iteration < iter
if (gaa < 0.000001) %检查满不满足条件gamma>0
n1 = length(miu(miu > rf(weeks)));
for s = 1:M %更新x0
if (miu(s) > rf(weeks))
x0(s) = 1 / n1;
end
end
%更新一个确保能继续迭代的x0(因为else中解出来是行向量)
DSR0 = DSR_a(weeks, wk_return_train, x0, rf);%更新dsr0
gaa = (miu' * x0 - rf(weeks)) / DSR0;
ga(iteration) = gaa; %更新gamma
else %正常情况
%ode hyperparameter
step = 0.0002;
t_end = 0.01;
tspan = 0:step:t_end; %求解区间
%解优化问题的常微分方程
[t,u] = ode15s(@(t,u) odepseudoNN(t, u, x0, P, q, I, miu, gaa, rf ,wk_return_train, weeks, 0.0001), tspan, x0);
u0 = u(end, :);
x0 = max(0, u0);%relu
x0 = x0';%换成列向量输出x0
DSR0 = DSR_a(weeks, wk_return_train, x0, rf);%更新dsr0
gaa = (miu' * x0 - rf(weeks)) / DSR0;%更新gamma
ga(iteration) = gaa;
end
%dsr_p(iteration) = DSR_p(weeks, wk_return_d1, x0, rf);
iteration = iteration + 1;
end %结束迭代
k = [1:15];
figure(1);%k次迭代中gamma的收敛情况
set(gcf, 'unit', 'centimeters', 'position', [10, 10, 16, 10])
linewidth_line = 1.8;
marksize = 5;
linewidth_gca = 0.8;
fontsize_gca = 20;
fontsize_label = 22;
fontsize_legend = 10;
plot(k , ga(1:15));
xlim([1 10])
xticks(0:1:10);
%h = legend('1', '2');
%set(h,'fontsize',fontsize_legend);
set(gca, 'linewidth', linewidth_gca, 'fontsize', fontsize_gca);
%set(gca, 'GridLineStyle', '--');
xlabel('${k}$', 'interpreter', 'latex', 'fontsize',fontsize_label);
ylabel('${gamma}$','interpreter', 'latex', 'fontsize',fontsize_label);
hold on
%figure(2);
%plot()
xk = x0;%整个函数的output
end
其他人总结的ode工具包: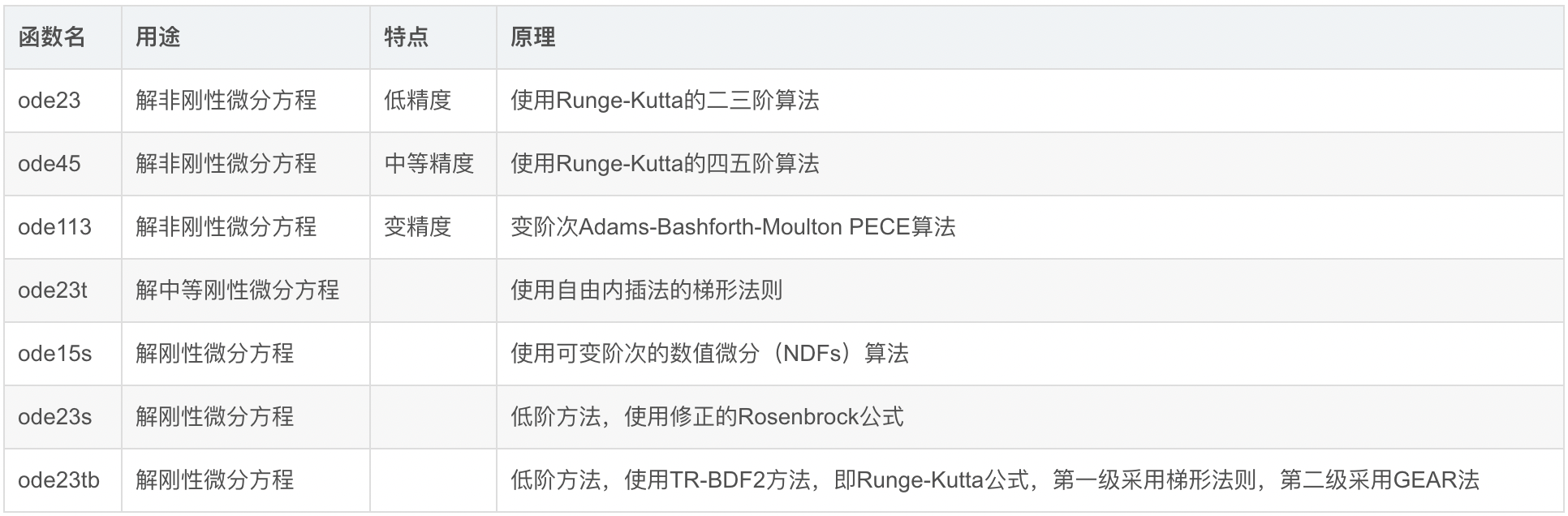
总结下来:先用ode45尝试,若长时间解不出来,换用ode15s
最后
以上就是安静西牛最近收集整理的关于Matlab 解常微分方程常用工具包的全部内容,更多相关Matlab内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复