曲率系列1：曲率、法曲率、平均曲率、主曲率和高斯曲率（概念推导解读）

93 阅读 0 评论 62 点赞

我是靠谱客的博主繁荣枕头，最近开发中收集的这篇文章主要介绍曲率系列1：曲率、法曲率、平均曲率、主曲率和高斯曲率（概念推导解读），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

高中数学解释的曲率：

曲率, 也即弯曲程度。
直观来想, 以一条连续光滑曲线上无限接近的两个点为端点的一段弧总应该可以看作是某圆上的一段弧，而这个圆的半径就被定义为曲线在这一点的曲率半径，而曲率则被定义为曲率半径的倒数。

也就是无穷小的一段弧长与其相对应弧度（也就是角度）的比值。（弧度的计算方法，就是用弧长除以半径r。以l表示弧长，r表示半径，α表示弧度，则α=l/r. 得到的是该弧所对圆心角的弧度值。）

则半径r计算公式是：

$r=frac{dl}{dalpha }$

曲率就是：

$k=frac{1}{r}$

因此：定义球体或者圆的“圆”的程度，术语叫做曲率，为：

$k=frac{1}{r}$

其中r为球体或者圆的半径，这样半径越小的圆曲率越大，直线可以看作半径为无穷大的圆，其曲率为：

$k=lim_{r->infty }frac{1}{r}$

（其实按照数学上导数的概念，曲率也很好解释啊，导数就是把曲线的一小段当成直线，所得直线的斜率。曲率半径就是把曲线的一小段当成圆，所得圆的半径。曲率就是曲率半径的倒数。因为半径越大的圆，弯曲程度越小嘛。）

其实可以想象比如地球，我们站在自己家无法感知他是圆的一样，因为半径太大啦。。。。。。

（一个圆半径越小，看起来就越弯曲；半径越大，看起来就越平，半径趋于无穷大，圆看起来就像一条直线，就几乎不弯曲了。所以我们把圆的半径的倒数，定义为曲率，因为我们希望曲率是一个衡量几何体弯曲程度的量。

对于一般的曲线，每点局部可以近似看成一小段圆弧（可以看其他答主提到的密切圆）。固定一点后，该点处密切圆弧的半径的倒数，就定义成曲线在该点处的曲率。注意，对于一般的曲线而言，不同点处的曲率数值并不一样，是个变数而不是常数。用数学术语来说，曲率是定义在曲线上的一个函数。——严格来说还可以讨论曲线曲率的正负号，但涉及曲线的定向问题，我不想画图所以不讨论了。）

--------------------------------------密切圆------------------------

将圆的曲率扩展到曲线的曲率上，就需要引入密切圆的概念：（一下内容参考：https://www.matongxue.com/madocs/2106/）

可以将圆的曲率扩展到曲线上。我们知道两点决定一条直线，比如下面就是曲线的割线：

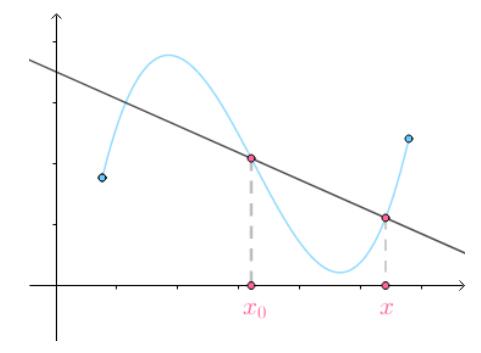当x趋于x0（ $xto x_{0}$ ）得到的是切线（也就是曲线上一点在该点处的切线）

同样的道理，三个点可以确定一个圆：

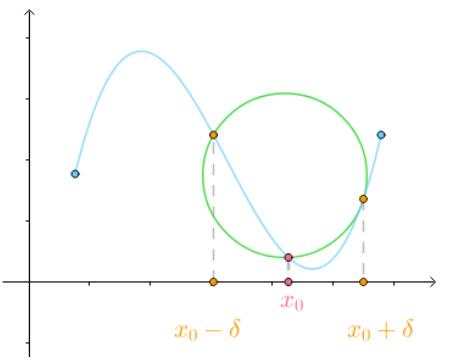当 $delta to 0$ 时（也就是三个点都近似于 $x_{0}$ 点），得到的圆称为密切圆（Osculating circle），是对 $x_{0}$ 附近的曲线的最佳圆近似。

有了密切圆就要知道密切圆的半径和曲率：

由上述圆的曲率与半径我们知道，在曲线较为平坦的地方，密切圆半径很大，较为弯曲的地方，密切圆半径就较小。因此，这个事实告诉我们，可以用密切圆的曲率来定义曲线的曲率。

首先引入正弦定理，一个三角形的外接圆：

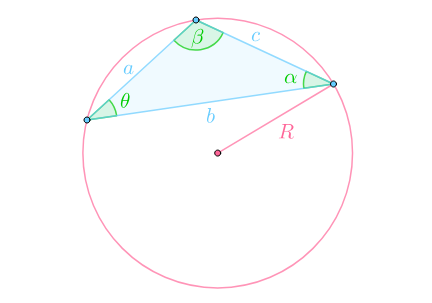
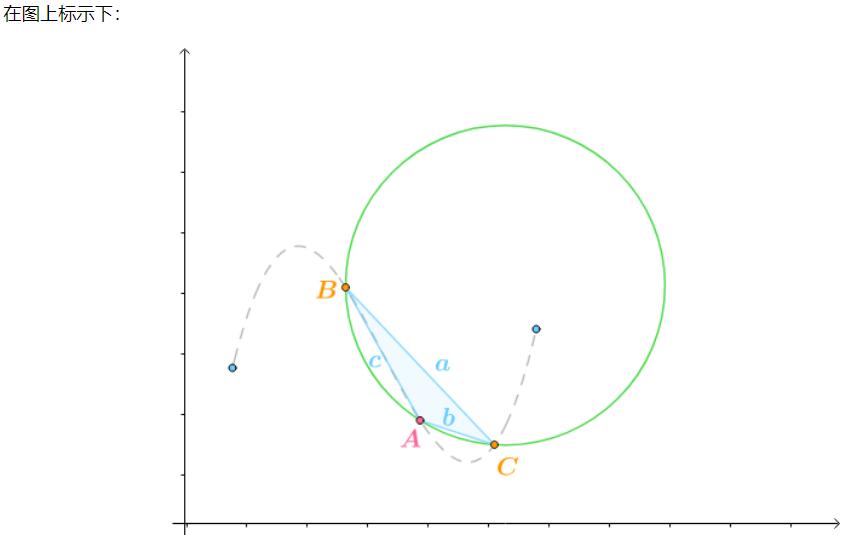
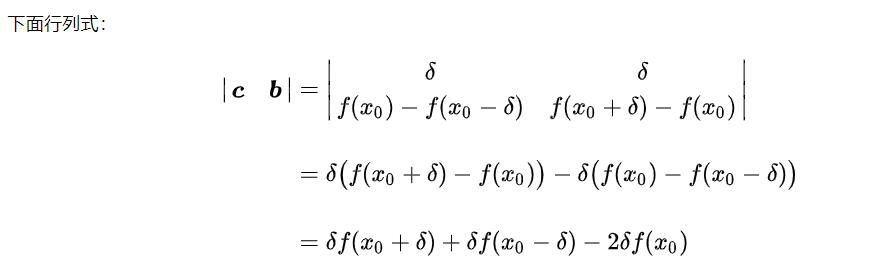
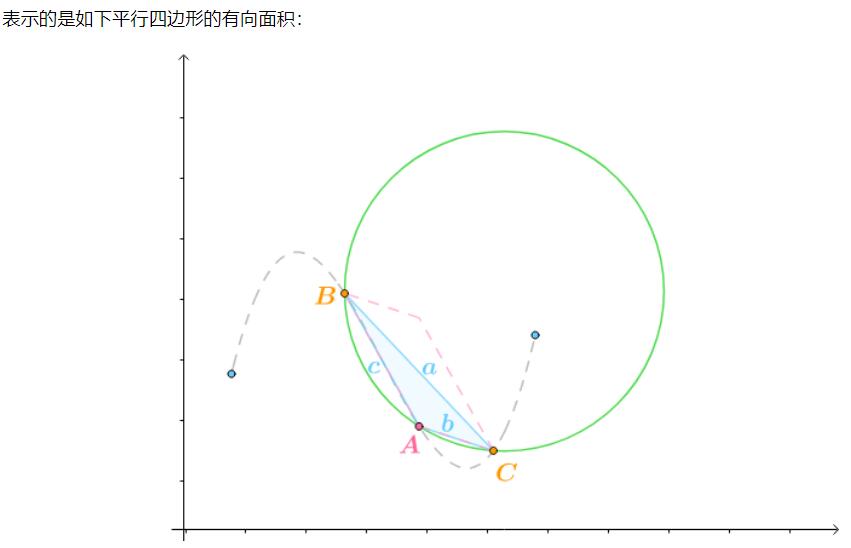
至此可以得到：

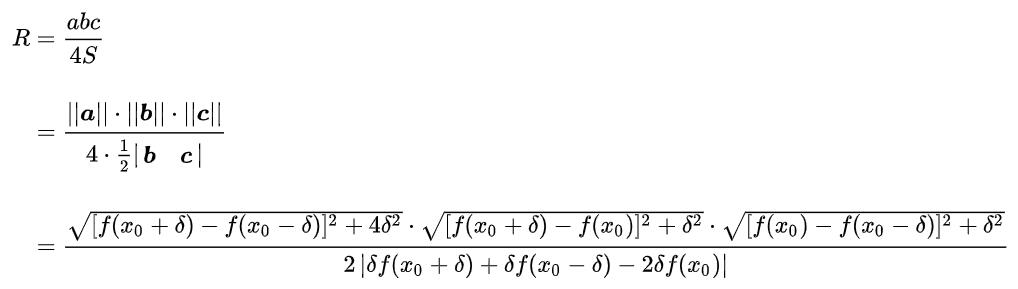
我们要求的密切圆的半径r，根据定义为：

$r=lim_{delta to 0}r$

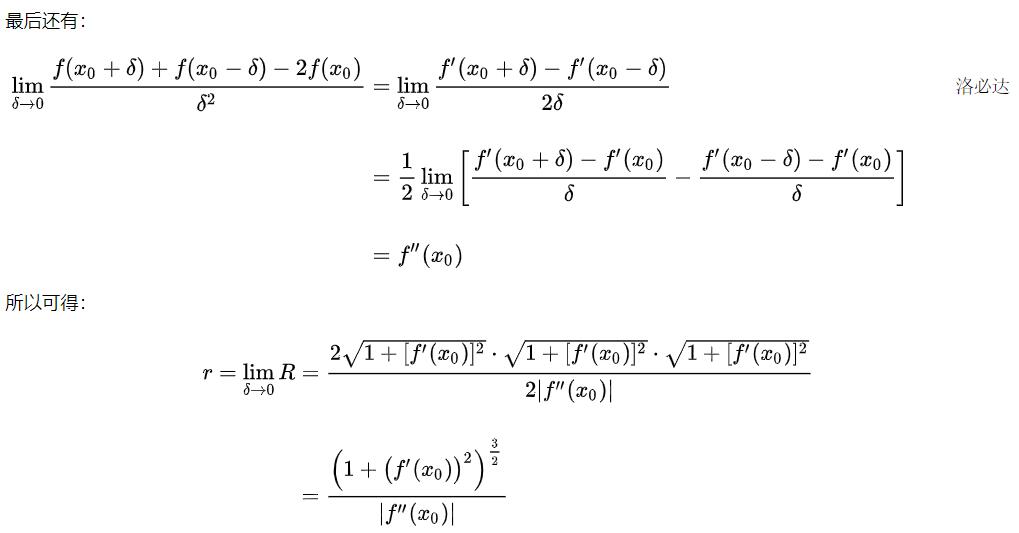
4 曲率圆的圆心

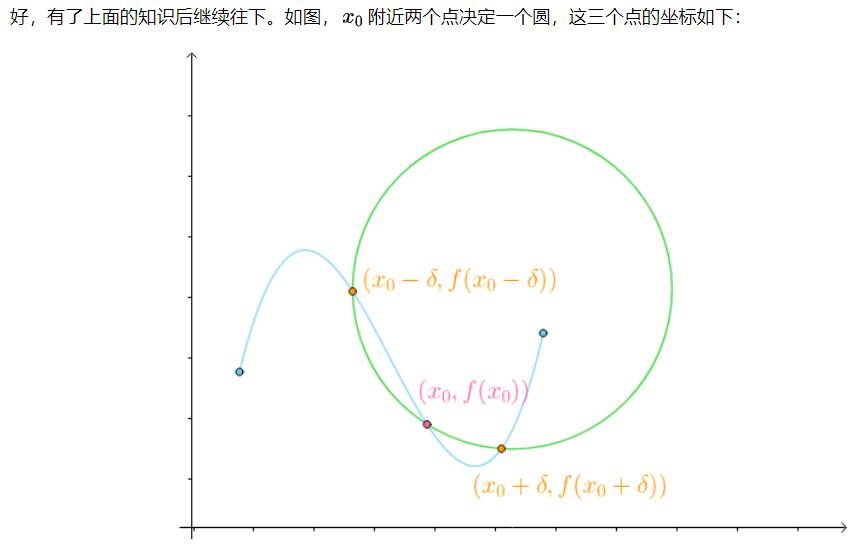
光知道半径是没有办法画出密切圆（曲率圆）的，还必须知道它的圆心在哪里：

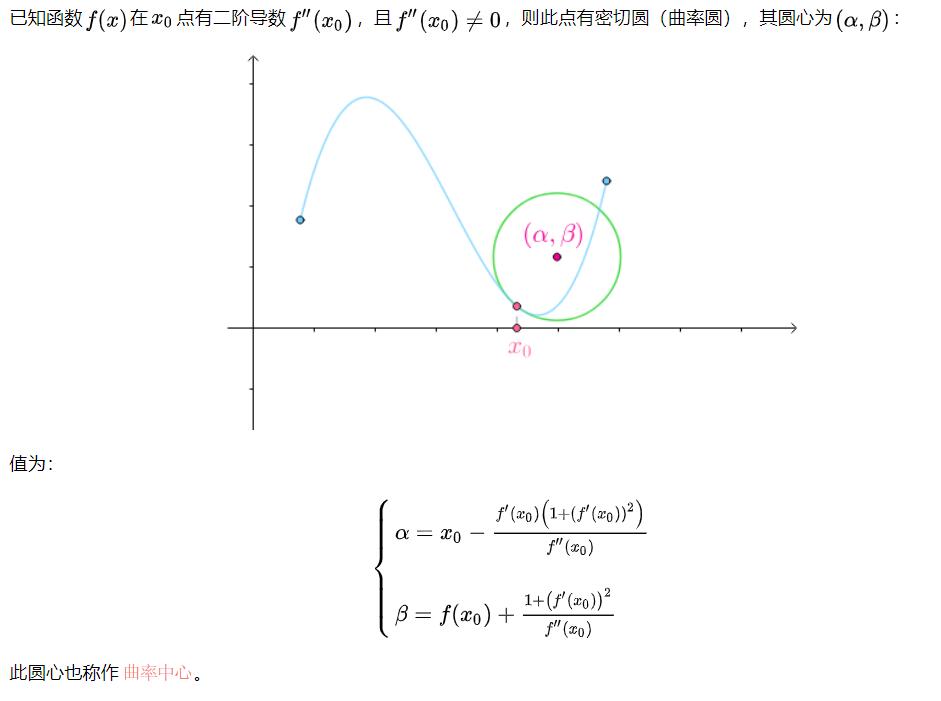
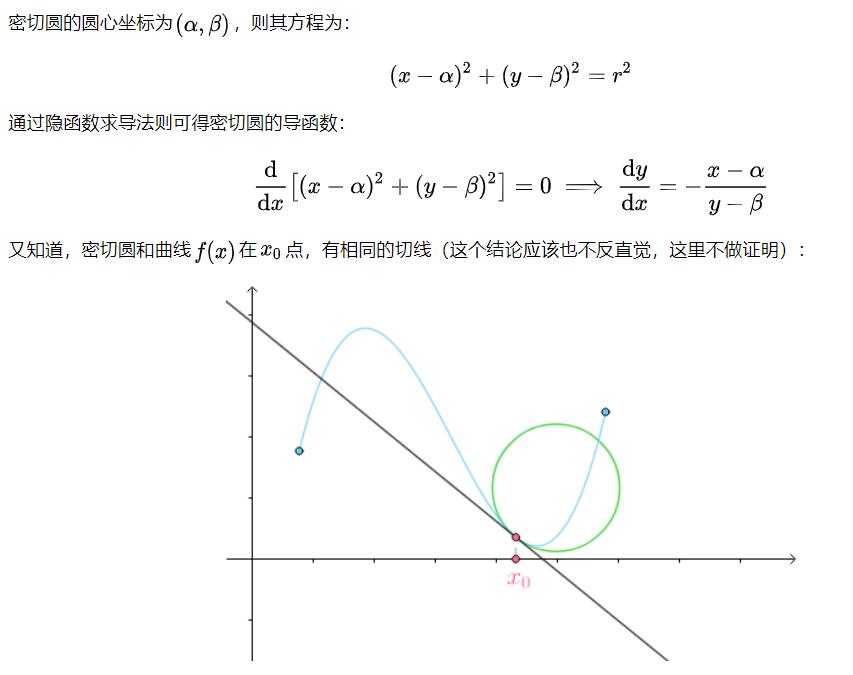
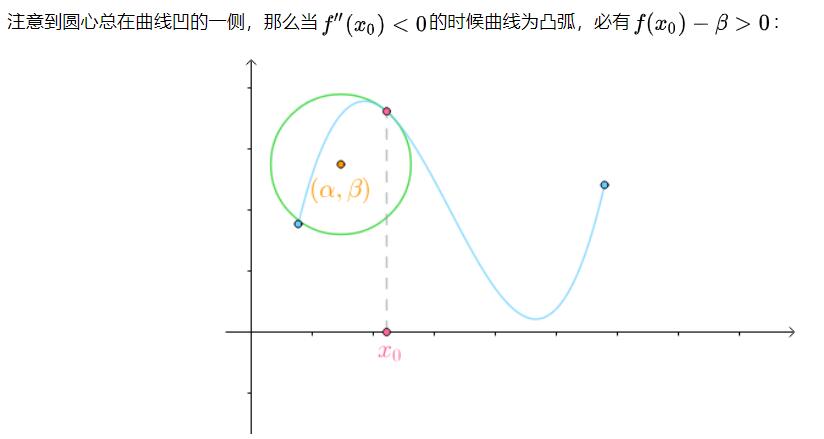
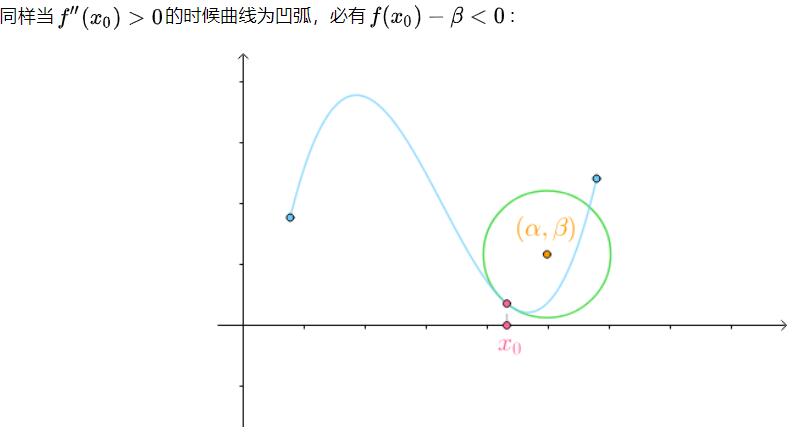
如果 $x_{0}$ 移动，会得到一系列曲线f(x)密切圆的圆心：

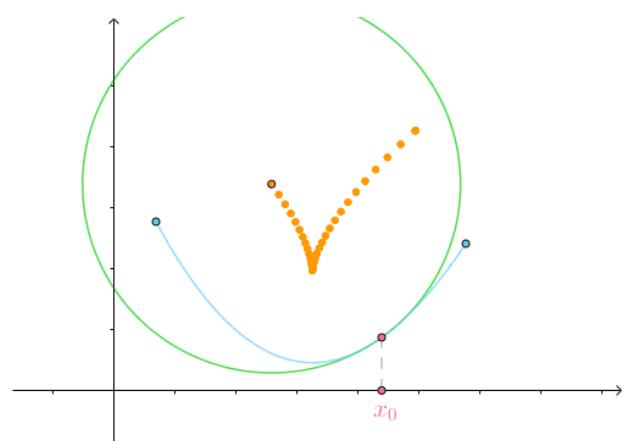绿色的为蓝色线上的点形成的圆，黄色的一系列点为各个圆的圆心。

1、法曲率：曲面在一点沿着不同方向的弯曲程度不同。或者说曲面离开切平面的速度不同。这个弯曲属性可以用这一点的沿着这个方法的法曲率刻画。

什么是法曲率？答：对曲面而言，固定一个点，沿着该点不同切方向截出的曲线的曲率，就是曲面沿着这个方向的法曲率。

2、主曲率：过曲面上某个点上具有无穷个正交曲率，其中存在一条曲线使得该曲线的曲率为极大，这个曲率为极大值Kmax，垂直于极大曲率面的曲率为极小值Kmin。这两个曲率属性为主曲率。他们代表着法曲率的极值。

什么是主曲率？答：法曲率中最大的与最小的，称为两个主曲率，对应的方向称为主方向。

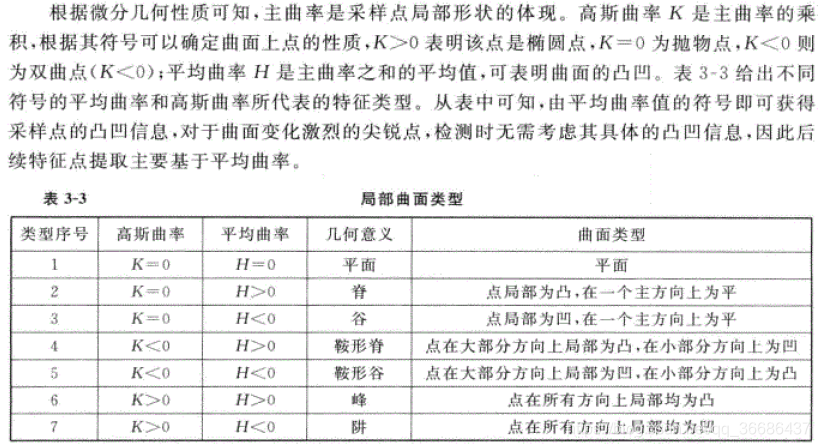
3、高斯曲率：两个主曲率的乘积即为高斯曲率，又称总曲率，反映某点上总的完全程度。

什么是高斯曲率？答：两个主曲率的乘积，称为曲面在该点处的高斯曲率——对的，就是那个德国数学大师高斯提出来的。高斯曲率不仅有数值的大小，也有自然而然的正负号，因为两个主方向对应的曲线可以弯向相同或者相反的方向。弯向相同的方向，比如球面，椭球面，就是正曲率，局部都位于切平面的同一侧；弯向相反的方向，比如马鞍面，或者薯片，就是负曲率，切平面的两侧都有曲面分布。当然，曲率本身是个函数（变数），他在同一张曲面上也是可以变号的。比如考虑环面（看成3维空间中的旋转曲面，而不是平坦环面），可以想想哪些点是正曲率，哪些点是负曲率。

4、平均曲率：是空间上曲面上某一点任意两个相互垂直的正交曲率的平均值。如果一组相互垂直的正交曲率可表示为K1,K2,那么平均曲率则为：K = (K1 +K2 ) / 2。

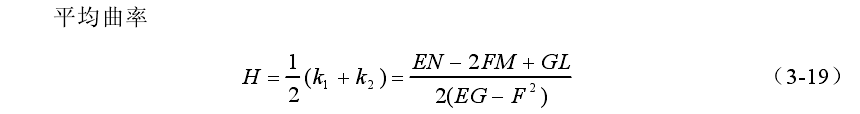
局部曲面类型：

参考书籍：海量点云数据处理理论与技术

详细解读参考链接：https://zhuanlan.zhihu.com/p/149584374

https://www.zhihu.com/question/303605875/answer/549326327

https://www.zhihu.com/question/30719930/answer/959904116

PS：

然后数学上还可以考虑更高维度的几何体，术语称为“流形”。3维以上流形，我们依然可以套用降维化归的想法，在流形上截出一个个子曲面，考虑这些子曲面的高斯曲率，术语称之为“截面曲率”，他们反映了流形沿着这些子曲面的弯曲信息。高维几何体的曲率的表达形式更加复杂，准确地说，流形上的曲率是个“张量”，而不仅仅是个数量——顺便提一句，流形上曲率张量这一整套理论，是另一个德国数学大师黎曼提出来的，所以同学们，不要小瞧德国的数学。不过讲到这里已经差不多到我通俗表达能力的极限了，要准确解释什么是“曲率张量”，然后通过曲率张量定义截面曲率，甚至准确定义什么是流形，我都得写数学定义、写公式了——而知乎上的文科生似乎不喜欢公式。。要准确理解最后一段提到的流形的曲率，您起码得学过数分、高代、微分流形理论、黎曼几何入门；不过理解曲线曲率，其实懂多元微分就行了，积分都不需要，文科生咬咬牙也是能做到的。

参考链接：https://www.zhihu.com/question/25952605/answer/713083818?