老卫带你学---模式分类中的特征融合方法以及各种方法的总结

概念、基本术语

信息融合：将来源不同的信息整合到一起，去冗余；得到的融合信息将利于我们之后的分析处理。
信息融合分为三个层次：数据融合，特征融合，决策融合。如下图所示：

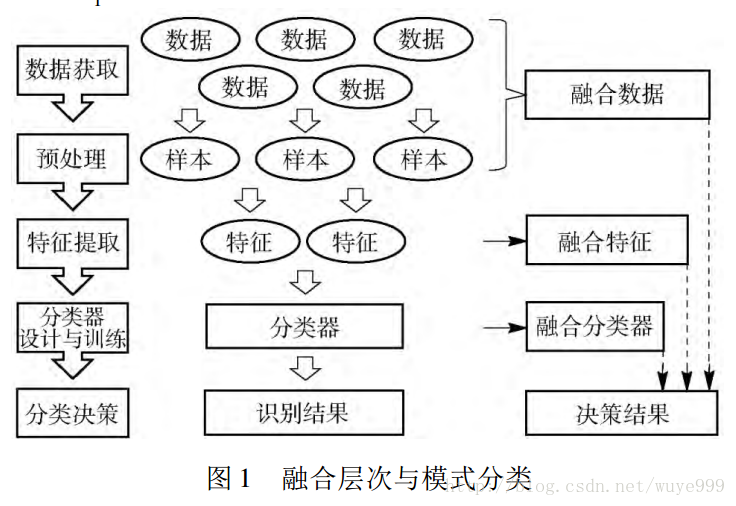
特征融合的分类

特征融合算法主要可以分为三类：
1.基于贝叶斯决策理论的算法
2.基于稀疏表示理论的算法
3.基于深度学习理论算法

基于贝叶斯理论的特征融合算法

已知模式空间包含种模式，记为:,未知样本由维实值特征组成，记为.根据最小错误率的贝叶斯决策理论，若将样本分为第类，则该类就是在已知样本条件下后验概率最大的模式类，这个决策过程可以表示为：

其中：表示第类的后验概率，

分类器的乘法规则和加法规则

假定将看做分类器的输出结果，就可以得到贝叶斯理论的的分类器融合算法。假定有个分类器，那么每个分类器都会输出一个结果,因此得到此时的特征为：.那么对于一个未知样本y，决策过程可以表示为：

其中：表示在已知个分类器输出结果的条件下第类的后验概率，.在此基础之上引入分类器独立性假设并结合下式：

就可以得到分类器融合的乘法规则：

上面这个会有一个问题，就是当为0时会出问题。再在乘法规则的基础上，再引入先验概率和后验概率近似相等：

其中：是一个很小的值。
最终可以推导出，分类器融合的加法规则：

基于线性特征依赖模型的特征融合算法

由于分类器独立性假设与先验概率和后验概率近似相等都有相应的成立条件，在一些场景中不一定通用。因此需要将其进行进一步泛化。这个公式有点多，就不贴上来的，主要的思路还是一样的。

基于稀疏表示理论的特征融合算法

稀疏表示的基本思想是使用数据稀疏这一先验知识，从一个超完备字典中找到尽可能少的原子对目标信号进行线性表示。稀疏表示问题可以表示为，对于向量和矩阵,我们希望找到一个向量,使得并且向量的的范数(0范数表示向量中非零元素的个数，1范数表示元素绝对值之和)要尽可能小。用公式表示为：

基于稀疏表示理论的特征融合算法是对样本提取多特征后建立特征联合稀疏矩阵，这个矩阵就是多特征融合的结果。就是将不同类型的特征的字典进行融合。

基于深度学习理论的特征融合算法

就是将多个神经网络得到的特征进行融合就得到了融合的特征。

总结方法：

对于经典的模式识别方法，我们都主要是按照预处理、特征提取、特征选择（降维）、训练分类器（或分类），后处理几部分构成。在实际操作中，我们会经常发现我们会将不同的特征结合起来共同使用。比如对于视频领域的Mo-SIFT特征其实就是将SIFT特征和光流特征结合而来。再比如对于人脸识别，我们很可能会将块纹理特征（和LBP、Haar）和梯度直方图特征结合。在这些结合中我们都产生了关于不同类型特征结合的朴素思想，最简单的就是将不同的特征连在一起编程一个特征向量。这些思想都是有效且合理的。在这篇博客中，我们仅仅将这些朴素的思想进行总结。

我们基于特征联合发生在模式识别的不同阶段，将其主要分为三个层次。第一个层次是特征层，第二个层次是特征分数层，第三个是分类结果层。对于每个不同层次又有数中简单可行的方法同大家分享。

1.第一层——特征层

特征层的思想就如上面我们举的例子一样，非常简单。把不同的特征联合在一起。但我们应该是什么是联合呢？假设我们有两类特征A和B，那我们是应该先将它们联合在一起形成一个统一的特征向量C，在对C进行特征选择（降维），还是先分别对A和B进行特征选择（降维）然后再将他们联合成为一个特征向量C呢？其实就是我们的特征联合应该是发生在降维前还是降维后的问题。在此，我们将发生在降维前的方法称为BFS（before feature selection），将先降维再联合的方法称为AFS（after feature selection）。我想这两种方法没有具体的优劣之分，具体问题具体分析。

2.第二层——特征分数层

其实我们在此是通过一系列的方法将两种特征归一化到相同指数。常用的有函数法，和概率密度法。

2.1 常用函数法。

我们常用的归一函数主要有一下几个：

（1）最大-最小函数。主要用于把原输入信号形状不变的拉伸或压缩到特定尺度。

（2）mean-std，即通过统计的只是将特征归一到统一均值和方差的一个范围中来。

（3）Med-MAD，他同mean-std比较类似。只不过这里采用中值Med和标准中值MAD代替了mean里面的均值和方差。标准中值即表示各个特征到中值的
距离所组成的距离集合的中值。

（4）双曲sigmoid函数。

（5）tanh函数

在此我们可以对tanh这种方法进行变型，让其具有统计的意义，如下所示

这里的Med和MAD也可以被均值和方差所替换

2.2 常用的概率密度估计方法。

其实这种方法总的来说就是用训练样本中的各个特征训练一组分类器，然后将分类器输出的概率值作为新的特征向量。举例如下：

我们有两种特征:A=[a1,a2,a3,a4…an]和B=[b1,b2,b3,b4…bm];

对于A特征，我们训练n个分类器记为f1,f2…fn，然后进行如下运算

xi = fi(ai) i=1.2.3…n

对于B特征，我们训练m个分类器记为g1.g2…gn,然后进行如下运算

yi = gi(bi) i = 1.2.3…n

在这里我们的两个分类器g和f选择为相同的模型，例如同为贝叶斯或者同为svm，并且不把分类器的输出设为类别，而为某一类别的概率。这样自然而然就可以得到概率密度作为联合的特征如下

C=[x1.x2.x3…xn.y1.y2.y3…ym]

3. 分类层

其实分类层的特征结合就是分别对不同类型的特征进行分类，然后结合分类的结果。这种结合方法里最朴素的应该就是投票或者二分类中的与（或）判别。投票呢就是分别对不同类别的特征进行分类，最终类别由各个分类器的分类结果进行投票决定。而与判别就是必须所有分类器都认为真，才最终判决为真。而或判决则是只要有任意一个分类器判决为真就为真。

更为复杂的我们可以将其与决策树或者boosting这样的分类器进行类比。

最后

以上就是感性小甜瓜为你收集整理的老卫带你学---模式分类中的特征融合方法以及各种方法的总结的全部内容，希望文章能够帮你解决老卫带你学---模式分类中的特征融合方法以及各种方法的总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。