姿态篇：四.非线性最小二乘与飞控传感器校准前言一.传感器校准简述二.传感器误差类型三.传感器校准的简单方式四.建立传感器误差模型五.求解误差方程六.高斯牛顿法七.Levenberg-Marquardt法八.传感器数据采集九.总结

[深入浅出多旋翼飞控开发][姿态篇][四][非线性最小二乘与飞控传感器校准]

Github
作者：Sky

前言

搞好了传感器，那意味着飞控已经完成了一半。

不用猜了，这句话正是鄙人说的:)。飞控的软硬件相关工作，绝大部分是围绕传感器展开的，它们的重要性，可能比你想象中的更大。

硬件上，为了寻找性能优秀又符合产品实际需求的传感器如陀螺仪、加速度计、磁力计等，我们经常需要对来自不同厂商的样品进行实际性能测试与评估，即使实际上常用的型号就那么几个。为了提升飞控的性能，许多传感器问题我们还需要从硬件上进行解决，如降低电源噪声、隔离机身震动甚至还要为传感器提供恒定温度的工作环境。

软件上，传感器校准、滤波与融合更是飞控程序中的重点，作为一名渣渣飞控工程师，浑浑噩噩工作数年，发现到头来大部分时间都是花在了传感器数据的处理上面，而且未来需要解决的问题，依然和传感器有关。

本篇文章将结合实际飞控代码，以循序渐进的方式向读者讲述，如何使用最优化算法，解决飞控中最基本的传感器校准问题。

飞控技术交流 562983648

一.传感器校准简述

飞控上会使用各种各样的传感器，但对于多旋翼而言，最核心的是陀螺仪无疑。离开了陀螺仪，你甚至无法让一架多旋翼飞行器正常离地。其次则是加速度计，提供姿态观测，让飞行器可以得到一个较为客观的自身姿态观测信息，使得自稳飞行成为可能（能够自动保持自身姿态水平或一定角度）。除此之外，还有许许多多的的其它传感器，共同为飞控提供稳定飞行所需要的数据。

其中，陀螺仪、加速度计和磁力计在飞行前（出厂前），均需要进行校准，才能达到正常工作所需要的性能。这便引出了一个问题：什么是传感器校准（标定）。

答案很简单，所有事物都不是非黑即白，而是时刻处于一个不可预知的混沌状态。工厂按照特定的技术及工艺标准制造生产出一批传感器，这些传感器中所有个体的实际状态处于一个随机分布且均值为期望误差的序列上。简单来说，我们买来10个传感器，这些传感器均存在着特定误差且这10个传感器的误差各不一致。这就要求我们在实际使用这些传感器时，需要对每一个进行单独的校准，得到特定的校准参数，从而正常发挥传感器的性能。

二.传感器误差类型

接下来我们会面临下面两个问题：

• 传感器有哪些误差
• 如何测量传感器的误差

如果从我们目前所使用的MEMS传感器的自身原理及制造工艺出发，分析传感器的误差来源，那可能需要长篇大论一番了，但那是超出作者能力的事情，也不是本篇文章所讨论的重点。

根据实际经验，我们可以把传感器误差分为两大类：

• 零偏误差（offset）
• 刻度误差（scale）

这两个是我们最容易理解，也是飞控中三大传感器均需要解决的误差类型，其中

零偏误差： 指传感器在零激励下的输出误差。如陀螺仪在静止状态下，其角速度测量值理论为0，而实际上我们将飞控静止放置，陀螺仪依然会输出诸如1°/s之类的数据，这便是该陀螺仪传感器的零偏误差。

刻度误差： 指传感器在一定激励输入下，其输出值与输入值的比值。比如我们将飞控放在一个以500°/s恒定角速度运动的转台上，而陀螺仪实际测量得到的角速度输出为495°/s，500 / 495 ≈ 1.01 便是该陀螺仪的刻度误差。

从上述说明中我们可以看出，要正确测量传感器的误差，必须向传感器施加特定的激励信号，通过比较传感器的实际输出与激励输入量，计算得到传感器的误差。

不同类型的传感器，所需要的激励信号源也不一样。如陀螺仪，要提供精确的激励信号，必须依靠专业的转台设备，这是个人及小公司均不具备的条件。好在对于大多数应用而言，陀螺仪的刻度误差在一个可以忍受的范围内，因此可被我们忽略。但对于精益求精的产品而言，要提升飞控性能到极致，刻度误差校准还是必须的，如某行业龙头，其飞控产品及整机产品，出厂前均需使用转台进行校准。缺少这些条件的个人爱好者，就只能暂时忽略这一项，只校准陀螺仪的零偏误差了，而大多数情况下，陀螺仪的零偏校准方式很简单，使用均值校准即可。因此，陀螺仪的校准不在本篇文章的讨论范围内。

而本文中讨论的重点：加速度计与磁力计，其信号激励源均来自于自然界，前者为地球的重力场，后者为地球的地磁场。

三.传感器校准的简单方式

1.加速度计

假设有下面的情形，我们将飞控水平放置于水平面，测得加速度计z轴输出值$g_1=0.97g$，然后将飞控翻转并同样水平置于水平面，再测得加速度计z轴输出值$g_2=-0.99g$。

设z轴零偏误差为$scal{e}_z$，刻度误差为$offse{t}_z$，已知实际重力加速度为g，可以得到下列两条等式：

• $(g_1-offse{t}_z)\ast scal{e}_z=g$
• $(g_2-offse{t}_z)\ast scal{e}_z=-g$

从而可以计算得到：

• $scal{e}_z\approx 1.02$
• $offse{t}_z=-0.01g$

将这个方法推广到其余两轴，便能得到其校准参数$scal{e}_x,scal{e}_y,offse{t}_x,offse{t}_y$。

缺陷：

这个校准方法较为简单，但是其可靠性建立于一个理想条件下：加速度计在采集每一个方向的数据时，必须严格贴合水平面。否则只能得到一个不太准确的校准数值。实际应用中，我们很难保证校准时让飞控的每一个面保持水平，因为飞行器本身就是一个不规则物体，更多时候我们采集到的加速度数据为$[0.05g,0.08g,0,95g]$，而非$[0,0,0.98g]$。或者说，这种方式的实现成本过高，难以实际应用。

2.磁力计

磁力计的简单校准方法原理等同于加速度计，即采集得到磁力计的三个轴的测量极值（最大与最小值），然后单独计算出每个轴的零偏误差与刻度误差。实现区别在于由于传感器激励信号源不一样，我们需要将磁力计在三维空间中进行各个方向的360°旋转，才能尽可能准确采集到极值。

缺陷：

实际应用中，磁力计校准对于飞行器使用者来说可能颇为频繁，而飞行器大小又各不一致，在很多情况下，我们是很难将飞行器翻来覆去地在各个方向上进行旋转，其可操作性非常低，且不方便普通用户的使用。如果旋转不全面，便无法采集到磁力计的真实极值，校准效果会大打折扣，甚至校准值严重偏离真实值。

四.建立传感器误差模型

对于程序员而言，解决实际问题的标准姿势如下：

提出实际问题—>建立数学模型—>转换为程序—>求解

而上一节中，我们描述了一个较为简单的用于加速度计与磁力计的校准方法，但是其前提条件较为苛刻，且校准效果不佳。于是，在这里我们提出了一个待解决的问题：找到一种使用便捷并且效果更好的校准算法。使用便捷，意味着约束条件越少越好，即在校准算法对传感器的采样点的数量和位置要求不能过于严格的情况下依然可以取得良好的校准效果。

为了解决这个问题，得到传感器的误差参数，首先我们需要建立传感器的误差模型，并将其转换为数学方程，从而进行求解。

以加速度计为例建立传感器误差模型

设三轴加速度计的零偏误差与刻度误差分别为
$$o_x,o_y,o_z,s_x,s_y,s_z$$
某一时刻该三轴加速度计的测量值分别为
$$x,y,z$$
设当前时刻真实加速度向量为
$$a=(a_x,a_y,a_z)$$
有以下关系：
$$\{\begin{array}{l}{a}_x=(x-o_x)s_x\\ a_y=(y-o_y)s_y\\ a_z=(z-o_z)s_z\end{array}$$

静止状态下，不管加速度计方向如何，其测量得到的加速度为重力加速度在各轴上的投影。而在地球上，重力加速度向量模值总是等于$1g$。假设$a_x,a_y,a_z$单位为$g$，便有以下等式成立：
$$a_x^2+a_y^2+a_z^2=1$$
即
$$(x-o_x{)}^2{s}_x^2+(y-o_y{)}^2{s}_y^2+(z-o_z{)}^2{s}_z^2=1$$

至此，我们将加速度计的误差求解转化成为了一个数学问题： 已知 $x,y,z$ ，由上一条等式，求解出 $o_x,o_y,o_z,s_x,s_y,s_z$

五.求解误差方程

上一节中，我们得到了传感器的误差方程：$(x-o_x{)}^2{s}_x^2+(y-o_y{)}^2{s}_y^2+(z-o_z{)}^2{s}_z^2=1$
求解方程，对于经历过九年义务教育的我们来说是一件非常熟悉的事情，但这里存在着几个棘手的问题：

• 该方程为六元二次方程，存在着6个未知数，如果只存在$x,y,z$一组观测值，那将会有无穷多解。因此我们需要获得多组观测值$x_i,y_i,z_i$，以构建方程组，从而求出唯一解，满足方程组里的每一个方程

• 对于六元二次方程而言，使用六组独立的观测值，构建出包含6个方程的方程组，理论上可以求出方程组的唯一解。可是事实上，我们从传感器上获取到的观测值，都是带有一定随机噪声的，即观测值并非完全准确，从而导致求得的方程解未必精确

• 使用计算机，我们可以轻松求出线性方程组的唯一精确解（如高斯消元法），而非线性方程问题，无论是从理论上还是计算方法上，都要复杂得多，大部分时候，对于无特定形式的非线性方程$f(x)=0$，是没有办法直接求得精确解的。

为了解决上述问题，这里引进了一种数学方法：最小二乘法

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

对于现实中的绝大部分问题，我们都是无法求得精确解的，于是退而求其次，使用最小二乘法，我们可以得到其近似解。

以传感器误差方程为例，设$r$为某特定解下方程的误差，有
$$r=1-(x-o_x{)}^2{s}_x^2+(y-o_y{)}^2{s}_y^2+(z-o_z{)}^2{s}_z^2$$
对于方程组而言，其误差的平方和函数为
$$S=\sum _{i=0}^n{r}_i^2$$
所谓最小二乘法，便是求得一组特定解，使得$S$最小(求函数极值)，该条件下的解，便是方程组的最优近似解。

对于线性方程组，可将误差函数$S=0$转换为矩阵方程并进行求解即可，可惜现实问题大部分均为非线性问题，如本文中的传感器误差方程便是一个非线性方程，是无法变换为矩阵方程形式的，因此我们必须换一个思路来解决问题。

假定该函数存在着局部最小值，那给定一个初始解，通过不断地迭代计算，从而找到误差平方和函数$S$的局部最优解，这便是非线性最小二乘的基本思想。

接下来，我们将讨论求解非线性最小二乘的具体算法。

六.高斯牛顿法

非线性最小二乘的求解算法有许多种，比较常见的有高斯牛顿法，Levenberg-Marquardt法（LM），DogLeg法等。其中高斯牛顿法是最为经典的一种算法，APM飞控中便是使用了该算法，而LM法可以看成是高斯牛顿法的改良版，鲁棒性更好，在实际工程中应用更广泛，天穹飞控中则使用了LM法。而LM法的基础部分和高斯牛顿法完全一致，因此我们从高斯牛顿法开始讲起。

由于算法原理细节部分较为复杂，需要用到大量公式，为了方便理解，将结合天穹飞控的实际代码进行讲解，高斯牛顿法和LM法的具体实现大部分是一样的，所以可以结合着来看。对于初学者来说彻底弄懂这一部分的原理对自己能力的提升帮助较大，因为此类最优化算法在飞控之外的非常多工程领域都是有着大量应用的，如计算机视觉和机器学习等。

天穹飞控中的LM法完整代码

要搞明白高斯牛顿法，我们要先来了解一下牛顿法

1.牛顿法

为求得函数最优解（极值点），牛顿法将问题转换为了求解$f^{{}^{\prime }}(x)=0$

首先给定一个初始解$x_0$，然后在$x_0$处进行一阶泰勒展开，得到
$$f^{{}^{\prime }}(x)\approx f^{{}^{\prime }}(x_0)+(x-x_0)f^{{}^{\prime \prime }}(x_0)$$
令
$$f^{{}^{\prime }}(x_0)+(x-x_0)f^{{}^{\prime \prime }}(x_0)=0$$
求解得到$x$，相比于$x_0$，有$f^{{}^{\prime }}(x)<f^{{}^{\prime }}(x_0)$，即新解$x$比初始解更接近最优解。当然该解和最优解之间还有一定未知的距离，于是我们将新解作为初始解，重复这一步骤，经过不断地迭代计算，最终会收敛于$f^{{}^{\prime }}(x)=0$。

牛顿法寻找极值点的动画示意图：

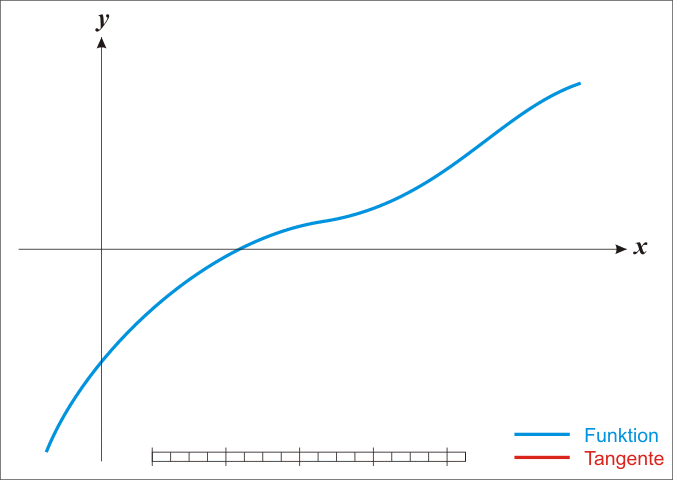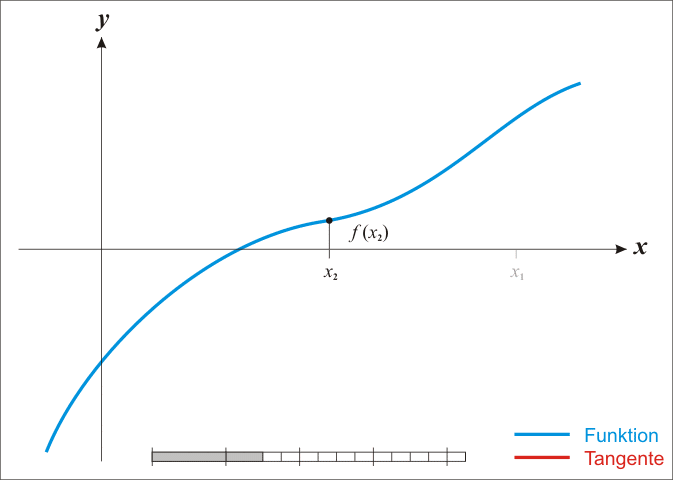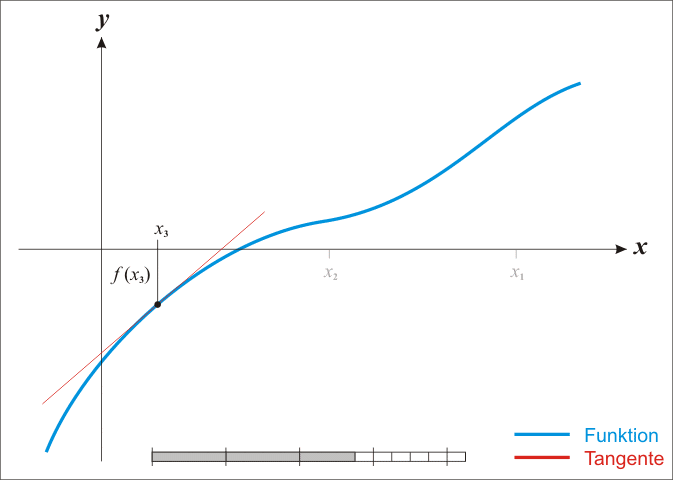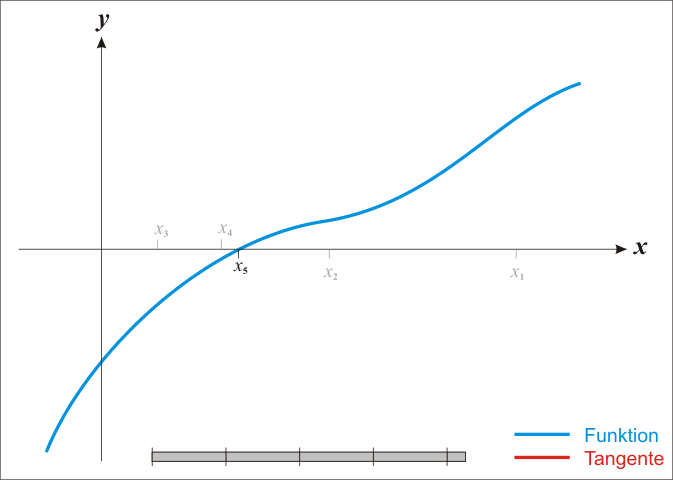
牛顿法的优点：

• 收敛速度快，且可用于求解任意连续函数的最优化问题

牛顿法的缺点：

• 可以看出，牛顿法实际上等同于寻找函数的局部极值点，因此必须选取一个相对接近的初始点，否则会导致无法正确收敛

• 需要求解目标函数的Hessian矩阵（二阶导）的逆矩阵，计算比较复杂

2.高斯牛顿法

高斯牛顿法是一种非线性最小二乘最优化方法。 其利用了目标函数的泰勒展开式把非线性函数的最小二乘化问题化为每次迭代的线性函数的最小二乘化问题

高斯牛顿法实际上是牛顿法的简化形式，或者说改进版。多维情况下，当维数较大时，牛顿法中的Hessian矩阵求逆是往往行不通的，而高斯牛顿法对牛顿法中的Hessian矩阵进行了化简，使得问题可解。

下面讲解高斯牛顿法的具体实现

首先定义目标函数
$$S(\beta )=\sum _{i=0}^5{r}_i^2(\beta )$$
其中
$$\beta =[{\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4,{\beta }_5]$$
对应了加速度计误差方程中的六个变量，即
$$[o_x,o_y,o_z,s_x,s_y,s_z]$$
而$r_i^2(\beta )$为传感器误差方程的误差平方和函数，即
$$r_i^2(\beta )=(1-(x_i-o_x{)}^2{s}_x^2+(y_i-o_y{)}^2{s}_y^2+(z_i-o_z{)}^2{s}_z^2{)}^2$$

设定一个初解${\beta }_{\alpha }$，将目标函数$S(\beta )$在${\beta }_{\alpha }$附近泰勒展开，并舍弃高阶无穷项，近似有：
$$S(\beta )=S({\beta }_{\alpha })+[▽S({\beta }_{\alpha }){]}^T(\beta -{\beta }_{\alpha })+\frac{1}{2}(\beta -{\beta }_{\alpha }{)}^T{H}_S({\beta }_{\alpha })(\beta -{\beta }_{\alpha })$$
我们的目标是求出特定解，使$S(\beta )$有最小值。当函数有最小值（属于极小值）时，其一阶导为0，即
$$▽S(\beta )=▽S({\beta }_{\alpha })+H_S({\beta }_{\alpha })(\beta -{\beta }_{\alpha })=0$$
从而得到了高斯牛顿法的迭代公式：
$$\beta ={\beta }_{\alpha }-[H_S({\beta }_{\alpha }){]}^{-1}▽S({\beta }_{\alpha })$$
设
$$△=[H_S({\beta }_{\alpha }){]}^{-1}▽S({\beta }_{\alpha })$$
则有
$$\beta ={\beta }_{\alpha }-△$$
这里便是迭代的关键了，给定初解后，每一次计算出$△$，便得到了一个新解，然后使用新解不断进行迭代计算，使其逐渐逼近最优解。

可能看到这里，你依然是一脸懵逼，但没有关系，你只需要知道，为了求解出函数的最优解，也就是传感器的最优校准参数，我们只需要不断去计算$△$就行了。

接下来便讲解如何计算$△$ (这里是整个算法实现的重点）

$△$中的$H_S$为$S$函数的Hessian矩阵（实际上是S函数的二阶导）
$$H_S=\left[\begin{array}{cccc}\frac{{\partial }^{2}S}{\partial {\beta }_0^2}& \cdots & \frac{{\partial }^{2}S}{\partial {\beta }_0{\beta }_5}& \\ ⋮& \ddots & ⋮& \\ \frac{{\partial }^{2}S}{\partial {\beta }_5{\beta }_0}& \cdots & \frac{{\partial }^{2}S}{\partial {\beta }_5^2}& \end{array}\right]$$
前文提到，高斯牛顿法对牛顿法所做的改进，便是对Hessian矩阵进行了简化，其中有
$$\frac{{\partial }^{2}S}{\partial {\beta }_i{\beta }_j}=2\sum _k(\frac{\partial r_k}{\partial {\beta }_i}\frac{\partial r_k}{\partial {\beta }_j}+r_k\frac{{\partial }^2{r}_k}{\partial {\beta }_i{\beta }_j})$$
忽略二阶微分项，近似有
$$\frac{{\partial }^{2}S}{\partial {\beta }_i{\beta }_j}=2\sum _k\frac{\partial r_k}{\partial {\beta }_i}\frac{\partial r_k}{\partial {\beta }_j}$$
于是有
$$H_S=2{\left[\begin{array}{cccc}\frac{\partial r_0}{\partial {\beta }_0}& \cdots & \frac{\partial r_0}{\partial {\beta }_5}& \\ ⋮& \ddots & ⋮& \\ \frac{\partial r_5}{\partial {\beta }_0}& \cdots & \frac{\partial r_5}{\partial {\beta }_5}& \end{array}\right]}^T\left[\begin{array}{cccc}\frac{\partial r_0}{\partial {\beta }_0}& \cdots & \frac{\partial r_0}{\partial {\beta }_5}& \\ ⋮& \ddots & ⋮& \\ \frac{\partial r_5}{\partial {\beta }_0}& \cdots & \frac{\partial r_5}{\partial {\beta }_5}& \end{array}\right]=2J_r^T{J}_r$$
这里的$J_r$实际上就是函数$r$（传感器误差方程的误差函数）的雅可比矩阵

$△$中的另外一个成员$▽S$为$S$函数的一阶导的列向量，即
$$▽S=\left[\begin{array}{c}\frac{\partial S}{\partial {\beta }_0}\\ ⋮\\ \frac{\partial S}{\partial {\beta }_5}\end{array}\right]$$
又有
$$\frac{\partial S}{\partial {\beta }_i}=\sum _k\frac{\partial (r_k^2)}{\partial {\beta }_i}=2\sum _k\frac{\partial r_k}{\partial {\beta }_i}{r}_k$$
故$bigtriangledown S $可改写为
$$▽S=\left[\begin{array}{c}\frac{\partial S}{\partial {\beta }_0}\\ ⋮\\ \frac{\partial S}{\partial {\beta }_5}\end{array}\right]=2{\left[\begin{array}{cccc}\frac{\partial r_0}{\partial {\beta }_0}& \cdots & \frac{\partial r_0}{\partial {\beta }_5}& \\ ⋮& \ddots & ⋮& \\ \frac{\partial r_5}{\partial {\beta }_0}& \cdots & \frac{\partial r_5}{\partial {\beta }_5}& \end{array}\right]}^T\left[\begin{array}{c}{r}_0\\ ⋮\\ r_5\end{array}\right]=2J_r^{T}r$$

于是我们终于得到了$△$的最终形式
$$△=[J_r({\beta }_{\alpha }{)}^T{J}_r({\beta }_{\alpha }){]}^{-1}{J}_r({\beta }_{\alpha }{)}^{T}r({\beta }_{\alpha })$$
或者换一个形式
$$J_r({\beta }_{\alpha }{)}^T{J}_r({\beta }_{\alpha })△=J_r({\beta }_{\alpha }{)}^{T}r({\beta }_{\alpha })$$
这就成了一个线性方程组，未知量是$△$，使用高斯消元法，便能求解出$△$的唯一解。

至此，高斯牛顿法的所有计算步骤均结束，我们只需要不断进行迭代计算：求解出$△$，从而得到新解$\beta$，然后进行下一次迭代，不断逼近函数最优解。

随着迭代次数的增加，最终会得到一个无限接近最优的解，但是考虑到时间成本和实际使用需求，在校准程序中我们设置一个阈值$eps$，当方程解达到一定精度时（定义为迭代步长的平方${△}^2<eps$），停止迭代，结束此次校准。

看完了，还是有点懵，怎么办？

下面贴上高斯牛顿法的完整实现代码，结合代码进行理解和分析，事半功倍，如果还没看懂，那就多看几遍。

主程序

/**********************************************************************************************************
*函 数 名: GaussNewton
*功能说明: 高斯牛顿法求解传感器误差方程，得到校准参数
*形    参: 传感器采样数据（6组） 零偏误差指针 比例误差指针 数据向量长度
*返 回 值: 无
**********************************************************************************************************/
void GaussNewton(Vector3f_t inputData[6], Vector3f_t* offset, Vector3f_t* scale, float length)
{
    uint32_t cnt    = 0;
    double   eps    = 0.000000001;
    double   change = 100.0;
    float    data[3];  
    float    beta[6];      //方程解
    float    delta[6];     //迭代步长
    float    JtR[6];       //梯度矩阵
    float    JtJ[6][6];    //Hessian矩阵
   
    //设定方程解初值
    beta[0] = beta[1] = beta[2] = 0;
    beta[3] = beta[4] = beta[5] = 1 / length;

    //开始迭代，当迭代步长小于eps时结束计算，得到方程近似最优解
    while(change > eps) 
    {
        //矩阵初始化
        ResetMatrices(JtR, JtJ);

        //计算误差方程函数的梯度JtR和Hessian矩阵JtJ
        for(uint8_t i=0; i<6; i++) 
        {
            data[0] = inputData[i].x;
            data[1] = inputData[i].y;
            data[2] = inputData[i].z;
            UpdateMatrices(JtR, JtJ, beta, data);
        }

        //高斯消元法求解方程：JtJ * delta = JtR，得到delta
        GaussEliminateSolveDelta(JtR, JtJ, delta);

        //计算迭代步长
        change = delta[0]*delta[0] +
                 delta[0]*delta[0] +
                 delta[1]*delta[1] +
                 delta[2]*delta[2] +
                 delta[3]*delta[3] / (beta[3]*beta[3]) +
                 delta[4]*delta[4] / (beta[4]*beta[4]) +
                 delta[5]*delta[5] / (beta[5]*beta[5]);

        //更新方程解
        for(uint8_t i=0; i<6; i++) 
        {
            beta[i] -= delta[i];
        }
            
        //限制迭代次数
        if(cnt++ > 100)
            break;
    }

    //更新校准参数
    scale->x  = beta[3] * length;
    scale->y  = beta[4] * length;
    scale->z  = beta[5] * length;
    offset->x = beta[0];
    offset->y = beta[1];
    offset->z = beta[2];
}

主程序中调用了三个子函数，其中：

• ResetMatrices，用于初始化矩阵变量

static void ResetMatrices(float JtR[6], float JtJ[6][6])
{
    int16_t j,k;
    for(j=0; j<6; j++) 
    {
        JtR[j] = 0.0f;
        for(k=0; k<6; k++) 
        {
            JtJ[j][k] = 0.0f;
        }
    }
}

• UpdateMatrices，用于计算求解$△$所用到的$J_r({\beta }_{\alpha }{)}^T{J}_r({\beta }_{\alpha })$(Hessian矩阵）和$J_r({\beta }_{\alpha }{)}^{T}r({\beta }_{\alpha })$这两个矩阵

static void UpdateMatrices(float JtR[6], float JtJ[6][6], float beta[6], float data[3])
{
    int16_t j, k;
    float dx, b;
    float residual = 1.0;
    float jacobian[6];
    
    for(j=0; j<3; j++) 
    { 
        b = beta[3+j];
        dx = (float)data[j] - beta[j];
        //计算残差 (传感器误差方程的误差)
        residual -= b*b*dx*dx;
        
        //计算雅可比矩阵
        jacobian[j] = 2.0f*b*b*dx;
        jacobian[3+j] = -2.0f*b*dx*dx;
    }
    
    for(j=0; j<6; j++) 
    {
        //计算函数梯度
        JtR[j] += jacobian[j]*residual;
        
        for(k=0; k<6; k++) 
        {
            //计算Hessian矩阵（简化形式，省略二阶偏导），即雅可比矩阵与其转置的乘积
            JtJ[j][k] += jacobian[j]*jacobian[k];
        }
    }
}

• GaussEliminateSolveDelta，使用高斯消元法求解$△$

static void GaussEliminateSolveDelta(float JtR[6], float JtJ[6][6], float delta[6])
{
    int16_t i,j,k;
    float mu;
   
    //逐次消元，将线性方程组转换为上三角方程组
    for(i=0; i<6; i++)
    {
        //若JtJ[i][i]不为0，将该列在JtJ[i][i]以下的元素消为0
        for(j=i+1; j<6; j++)
        {
            mu = JtJ[i][j] / JtJ[i][i];
            if(mu != 0.0f) 
            {
                JtR[j] -= mu * JtR[i];
                for(k=j; k<6; k++)
                {
                    JtJ[k][j] -= mu * JtJ[k][i];
                }
            }
        }
    }

    //回代得到方程组的解
    for(i=5; i>=0; i--)
    {
        JtR[i] /= JtJ[i][i];
        JtJ[i][i] = 1.0f;
        
        for(j=0; j<i; j++)
        {
            mu = JtJ[i][j];
            JtR[j] -= mu * JtR[i];
            JtJ[i][j] = 0.0f;
        }
    }

    for(i=0; i<6; i++)
    {
        delta[i] = JtR[i];
    }
}

事实上，在实际应用中使用高斯牛顿法，会出现许许多多的问题，因此下面介绍一种基于高斯牛顿改良优化而来的算法。

七.Levenberg-Marquardt法

实际应用中，高斯牛顿法有着如下缺点：

• 初始点选取较为严苛，若初始点距离极小值点过远，迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值
• 高斯牛顿法中的Hessian矩阵在某些情况下可能是非正定的（不可逆）
• 残差$r$过大时可能导致高斯牛顿法无法收敛

而Levenberg-Marquardt法（LM法，又称阻尼最小二乘法）改善了高斯牛顿法的不足之处，并结合了高斯牛顿法和梯度下降法的优点，而实际上所做的改动非常小。

在高斯牛顿法中，迭代步长$△$被定义为
$$△=[H_S({\beta }_{\alpha }){]}^{-1}▽S({\beta }_{\alpha })$$
而在LM法中，加入了阻尼因子$\mu$，有
$$△=[H_S({\beta }_{\alpha })+\mu I{]}^{-1}▽S({\beta }_{\alpha })$$
从而消除了Hessian矩阵非正定的情况，更重要的是迭代过程中阻尼因子$\mu$是可变的，用于调整下降方向，当：

• $\mu$趋近于0时，算法退化为高斯牛顿法
• $\mu$很大时，效果相当于梯度下降法

使用LM法时， 需要加入一些$\mu$的调整策略，使得距离解较远的时候，使用梯度下降法，距离极小值较近的时候，使$\mu$减小，这样就近似高斯牛顿法，能得到比梯度下降法更快的收敛速度。

算法的具体实现这里就不贴出来了，可以到这里查看：天穹飞控中的LM法

八.传感器数据采集

前几节介绍了如何使用非线性最小二乘法校准传感器，下面简单说明校准时采集所需传感器数据的具体步骤。

1.加速度计

在天穹飞控中，加速度校准使用标准的六面采集法，需要将飞控按照上、下、前、后、左、右六个方向静止放置一段时间（2s左右），顺序随意且飞控方向大致准确即可，飞控自动检测当前加速度计方向，并采集多组数据取平均值，最后得到6组方向各异的数据，导入LM校准函数，便能求出加速度计的6个校准参数。

加速度校准采集代码

天穹飞控兼容mavlink，可以使用QGroundControl地面站完成加速度计的校准步骤，如下图：

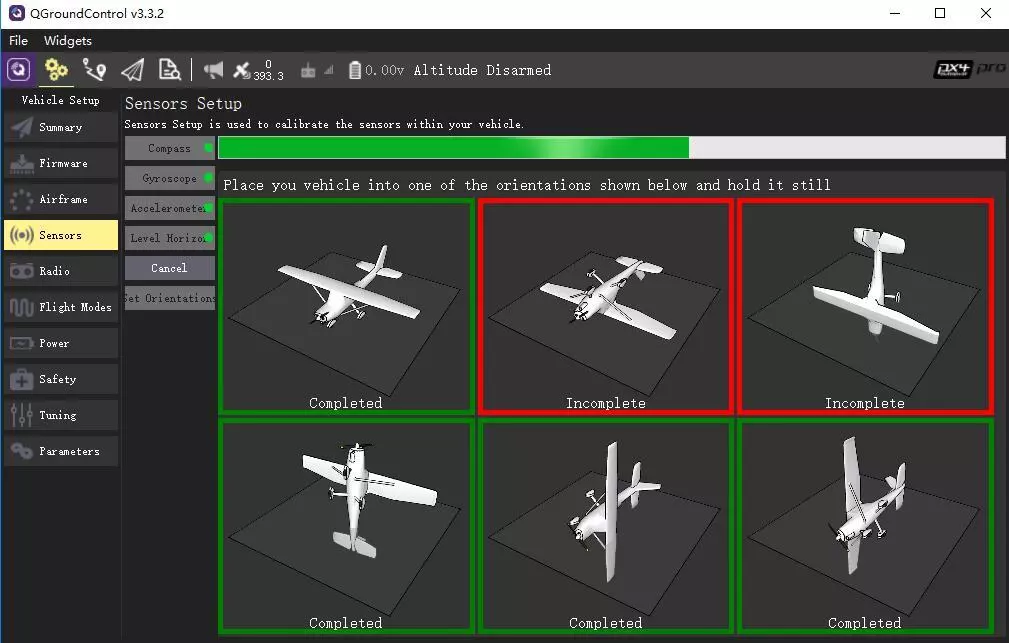
点击左侧的Accelerometer按钮，确认OK，飞控便会进入加速度校准流程，同时QGC会显示出当前校准进度以及图片提示，当对应方向采集数据完毕时，对应图片外框会变绿，红色的则是还没有采集数据的方向。

2.磁力计

磁力计的数据采集方式采用比较通用的两圈旋转方式，即：将飞控水平旋转一圈，然后再竖直旋转一圈。在这个过程中，记录下各轴的最大和最小值数据。

磁力计校准采集代码

同样可以使用QGC进行磁力计校准，点击Compass并确认OK。开始按照上述步骤旋转飞控，完成校准。

然而相对加速度计校准而言，磁力计校准对算法的要求更高。由于加速度计校准环境通常比较单一，且静止状态下加速度计数据基本不受外界干扰，所以采集到的数据都是比较准确的，使得算法很容易收敛，实测大概只需4-5次的迭代运算，就可以达到所需精度。

而磁力计数据采集在实际应用过程中，可能存在以下问题：

• 校准环境比较复杂，而且校准频率非常频繁。用户可能是在室内校准，也可能是在城市的建筑间校准，或者是在充满了未知磁场干扰的环境下校准。这便导致了在校准期间，可能由于各种未知的外部干扰，使得磁力计数据采集出现“野值”

• 为了简化校准步骤，我们采用了较为简单的两圈旋转方式，但由于地磁场的分布方向原因，实际上这样我们采集到的磁力计数据并不是在整个球面上分布均匀的，如下图所示（图片来自正在开发中的天穹地面站）：
  
  为了解决问题1，我们对采集到的数据做了一定的滤波平滑处理，同时实时计算数据的一个平均模值，当新值的大小超过平均模值一定比例时，抛弃这个值，避免在构建误差方程组时，引入包含较大干扰量的观测值，导致算法无法收敛或最终计算出来的传感器校准参数存在误差。

问题2考验了算法的性能，即在样本分布不均匀的情况下是否依然可以收敛，经过测试和验证，天穹飞控中使用的LM法是能够经受得住这个考验的。

九.总结

本篇文章介绍了飞控中最基本的传感器误差问题，并提出了有效的解决方法。其中所使用到的非线性最小二乘算法，在现代计算机工程领域有着非常广泛的应用，所以即使对飞控技术兴趣不大的童鞋，本文也是值得一看的。

而对于我们的飞控而言，完成了传感器基本误差的校准，只是相当于迈出了第一步，后面还有无数难题待解决，再接下来的教程中，会陆续针对不同的问题寻求最优的解决方案，当然由于本人水平有限，只能起到抛砖引玉的作用，希望有更多的有识之士，加入这个开源飞控项目，一起完善，共同进步。

最后

以上就是虚心纸鹤为你收集整理的姿态篇：四.非线性最小二乘与飞控传感器校准前言一.传感器校准简述二.传感器误差类型三.传感器校准的简单方式四.建立传感器误差模型五.求解误差方程六.高斯牛顿法七.Levenberg-Marquardt法八.传感器数据采集九.总结的全部内容，希望文章能够帮你解决姿态篇：四.非线性最小二乘与飞控传感器校准前言一.传感器校准简述二.传感器误差类型三.传感器校准的简单方式四.建立传感器误差模型五.求解误差方程六.高斯牛顿法七.Levenberg-Marquardt法八.传感器数据采集九.总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。