经典论文回顾: Colorization using Optimization

经典论文Colorization using Optimization来自于siggraph2004，论文旨在通过简单的交互实现灰度图的全局彩色化，论文短小精悍、思路新颖、实现简单、效果优良。短短6页纸的论文，引用1300+。

论文链接：https://webee.technion.ac.il/people/anat.levin/papers/colorization-siggraph04.pdf
代码链接：https://github.com/lightalchemist/colorize-image

输入：原始灰度图 （下图第一张图） + 局部着色（下图第二张图）
输出：全局着色效果（下图第三张图）

算法工作在YUV空间，简单来讲，YUV适用于电视信号传输，Y表示亮度，UV表示色度。YUV与RGB颜色空间的相互转化参见：https://www.jianshu.com/p/cf583040c930。论文核心思想：亮度近似的像素应当具有相近的颜色。

两个核心能量公式如下所示：

$$J(U)=\sum _r(U(r)-\sum _{s\in N(r)}{w}_{rs}U(s){)}^2\text{\hspace{1em}(1)}$$

$$J(V)=\sum _r(V(r)-\sum _{s\in N(r)}{w}_{rs}V(s){)}^2\text{\hspace{1em}(2)}$$

这里， $s$是$r$的邻居，一般限定在一个3*3的邻域内， $w_{rs}$是像素 $r$ 和 $s$ 根据 Y通道计算的相似度， 并且有 ${\sum }_{s\in N(r)}{w}_{rs}=1.0$， $w_{rs}$计算公式如下：

$$w_{rs}=exp(-(Y(r)-Y(s){)}^2/2{\sigma }_r^2)\text{\hspace{1em}(3)}$$

以上述公式(1)为例，其实等效于求解一个大型线性方程数组 $Ax=b$，(2)的解法是一样的，下面对这个过程进行推导。

公式(1)其实是一些平方项的和，我们令:
$$\{\begin{array}{r}K(1)=U(1)-\sum _{s\in N(1)}{w}_{rs}U(s)\\ K(2)=U(2)-\sum _{s\in N(2)}{w}_{rs}U(s)\\ ...\\ K(n)=U(n)-\sum _{s\in N(n)}{w}_{rs}U(s)\end{array}\text{\hspace{1em}(4)}$$
那么，$K=[K(1),k(2),...,K(n){]}^T$ 可以写成如下的线性方程组的形式 (如果 $j\notin N(i),w_{ij}=0$)：
$$K=\left[\begin{array}{cccc}1& -w_{12}& ...& -w_{1n}\\ -w_{21}& 1& ...& -w_{2n}\\ .& .& .& .\\ .& .& .& .\\ -w_{n1}& -w_{n2}& ...& 1\end{array}\right]\left[\begin{array}{c}U(1)\\ U(2)\\ ..\\ ..\\ U(n)\end{array}\right]\text{\hspace{1em}(5)}$$
公式(1)实际对应$K$中每一项的平方和，也就是：
$$J(U)=\sum _{i=1}^{n}K(i{)}^2=K^{T}K\text{\hspace{1em}(6)}$$

令(5)中包含权重的稀疏矩阵为$L$, 那么上式(6)可以进一步改写为：
$$J(U)=K^{T}K=(LU{)}^T(LU)=U^T{L}^{T}LU\text{\hspace{1em}(7)}$$
其中，$U=[U(1),U(2),...U(n){]}^T$是待求的未知量, 接下来对上式求导：
$$\frac{\partial J(U)}{\partial U}=2L^{T}LU\text{\hspace{1em}(8)}$$
令导数等于0，得到关于$U$的齐次线性方程组：
$$L^{T}LU=0\text{\hspace{1em}(9)}$$

可以直接计算上述方程组, 但需要计算大型矩阵的乘积$L^{T}L$较为不便，因此一般不这样求，而是改为计算：
$$LU=0\text{\hspace{1em}(10)}$$

那么，一个问题是(9)跟(10)是否等价呢？也就是两个方程是否同解呢？看上去等式(10)成立，等式(9)必然成立，那么(9)能否推出(10)呢？ 答案是肯定的。

我们对一般的情况进行推导，即证明 (i) $A^{T}AX=0$ 与 (ii) $AX=0$ 同解。因为(ii) $\to$ (i)是显然的，所以只推 (i) $\to$ (ii).
$$A^{T}AX=0\to X^T{A}^{T}AX=0\to (AX{)}^T(AX)=0$$

令 $Y=AX=[y_1,y_2,...,y_n{]}^T$, 那么 $(AX{)}^T(AX)=y_1^2+y_2^2+...+y_n^2=0\to y_i=0\to AX=0$, 所以(i)(ii)同解。

所以最终只需要计算（10）所示的线性方程组即可。

需要说明的是，线性方程组 $LU=0$ 中的 $L$ 是Laplacian矩阵，不满秩，有无穷解。 需要用户涂鸦给定一些颜色才能求解，实际上该欠约束的线性方程组 (10) 添加约束。

构建线性系统的核心代码为：

//Y:Y通道（灰度图本身的灰度值）, scribbles: 用户着色的图，mask：着色区域的mask
//A：系数矩阵，bu，bv关于U/V方程组的右侧列矩阵
void setupProblem(const cv::Mat& Y, const cv::Mat& scribbles, const cv::Mat& mask, 
                  Eigen::SparseMatrix<double, Eigen::RowMajor>& A, Eigen::VectorXd& bu,
                  Eigen::VectorXd& bv, double gamma)
{
    typedef Eigen::Triplet<double> TD;

    auto nrows = Y.rows;
    auto ncols = Y.cols;
    auto nPixels = nrows * ncols;
    A.resize(nPixels, nPixels);

    std::vector<TD> coefficients;
    coefficients.reserve(nPixels * 3);
    bu.resize(nPixels);
    bv.resize(nPixels);
    bu.setZero();
    bv.setZero();

    cv::Mat yuvScribbles;
    cv::cvtColor(scribbles, yuvScribbles, cv::COLOR_BGR2YUV);
    yuvScribbles.convertTo(yuvScribbles, CV_64FC3);
    std::vector<cv::Mat> channels;
    cv::split(yuvScribbles, channels);
    cv::Mat& U = channels[1];
    cv::Mat& V = channels[2];

    // TODO: See if we can do this more efficiently using matrix reshape
    std::vector<double> y, u, v;
    std::vector<bool> hasColor;
    to1D(Y, y);
    to1D(U, u);
    to1D(V, v);
    to1D(mask, hasColor);

    const int numNeighbors = 8;
    std::vector<double> weights;
    weights.reserve(numNeighbors);
    std::vector<unsigned long> neighbors;
    neighbors.reserve(numNeighbors);
    for (auto i = 0; i < nrows; ++i) {
        for (auto j = 0; j < ncols; ++j) {
            unsigned long r = i * ncols + j;
            getNeighbours(i, j, nrows, ncols, neighbors);
            getWeights(y, r, neighbors, weights, gamma);
            coefficients.push_back(TD(r, r, 1));
            for (auto k = 0u; k < neighbors.size(); ++k) {
                auto s = neighbors[k];
                auto w = weights[k];
                if (hasColor[s]) {
                    // Move value to RHS of Ax = b
                    bu(r) += w * u[s];
                    bv(r) += w * v[s];
                } else {
                    coefficients.push_back(TD(r, s, -w));
                }
            }
        }
    }

    A.setFromTriplets(coefficients.begin(), coefficients.end());
}

下面给一个直观的例子：我们给出一个2行3列的图像, 现在灰度图上进行了局部着色，如(2)所示，可以抽出着色部分的U通道，接下来我们的任务是求解其他部分的U值，如(3)所示，剩余的$x_2,x_3,,x_4,x_6$ 是待求解的未知数。V值求解方法一样，灰度图的灰度值本身就是Y，最后我们把YUV合起来就得到了最终的彩色图。

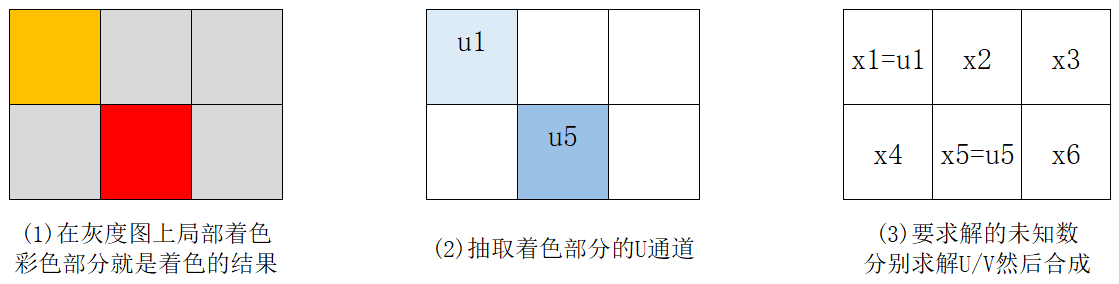
对于$x_1$：因为这里已经被着色，那么必然有： $x_1=u_1$
对于$x_2$：有5个邻居，邻域U的加权平均等于$x_2$本身的U值， 因此 $x_2-w_{21}{u}_1-w_{23}{x}_3-w_{24}{x}_4-w_{25}{u}_5-w_{26}{x}_6=0$
对于$x_3$：有3个邻居， $x_3-w_{32}{x}_2-w_{35}{u}_5-w_{36}{x}_6=0$
对于$x_4$：有3个邻居， 因此有： $x_4-w_{41}{u}_1-w_{42}{x}_2-w_{45}{u}_5=0$
对于$x_5$：因为这里已经被着色，那么必然有： $x_5=u_5$
对于$x_6$：有3个邻居， 因此有： $x_6-w_{62}{x}_2-w_{63}{x}_3-w_{65}{u}_5=0$

那么，上式可以写成如下的线性系统：(核心就是将上面各式的已知量全部移到右侧，未知量全在左侧)

$\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& -w_{23}& -w_{24}& 0& -w_{26}\\ 0& -w_{32}& 1& 0& 0& -w_{36}\\ 0& -w_{42}& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& -w_{62}& -w_{63}& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\end{array}\right)=\left(\begin{array}{c}{u}_1\\ w_{21}{u}_1+w_{25}{u}_5\\ w_{35}{u}_5\\ w_{41}{u}_1+w_{45}{u}_5\\ u_5\\ w_{65}{u}_5\end{array}\right)$

最后

以上就是无聊百褶裙最近收集整理的关于经典论文回顾: Colorization using Optimization的全部内容，更多相关经典论文回顾:内容请搜索靠谱客的其他文章。