GAMES101笔记（二）一、 纹理映射二、几何三、曲线

目录

一、 纹理映射

Mipmap

环境光照

 凹凸贴图

Bump Maps

Displacement Maps

阴影贴图Shadow Maps

软硬阴影

二、几何

三、曲线

贝塞尔曲线

样条曲线

 曲面

Catmull-Clark Subdivision (General Mesh)

一、 纹理映射

将三维物体上的任意一个点都映射到一个2维平面之上

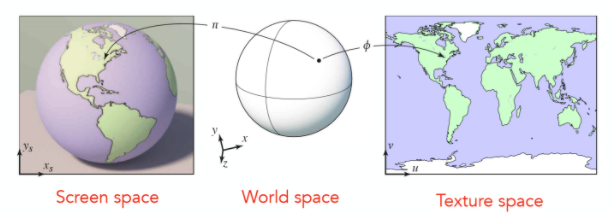
 在纹理空间之内任意一个二维坐标都在[0,1]之内。横轴和纵轴的最大值都为1，一幅Texture上的任意一点都可以用一个(u,v)坐标来表示(0<=u<=1,0<=v<=1),因此只需要在三维world space中每个顶点的信息之中存储下该顶点在texture space的(u,v)坐标信息，自然而然的就直接的得到了这种映射关系。

纹理过小引发的问题：导致走样失真

解决：双线性插值

纹理过大引发的问题：导致近处锯齿！远处摩尔纹！

 解决：超采样

Mipmap

范围查询

Mipmap就是从一张图生成一系列图，例如有一张纹理为128*128，称之为第0层纹理，我们可以生成更多更高层的纹理，每一层都是上一层缩小到一半的结果。例如第0层为 ，第一层为 ，第二层为32*32，直到最后变成一个像素，这样一共就有log层。

环境光照

环境光照，也有叫环境光映射或者环境贴图。

 正常来讲，我们记录环境光信息不能只记录方向，物体在空间内的不同位置会有不同的环境光效果，但是这里在环境光贴图中只记录环境光的方向。

环境光是怎么得到的呢？我们可以在空间中放一个镜面球，它所反射出来的就是环境光。因此我们可以把环境光存储在一个球上，然后把它展开得到环境光贴图。这就是Spherical Environment Map。

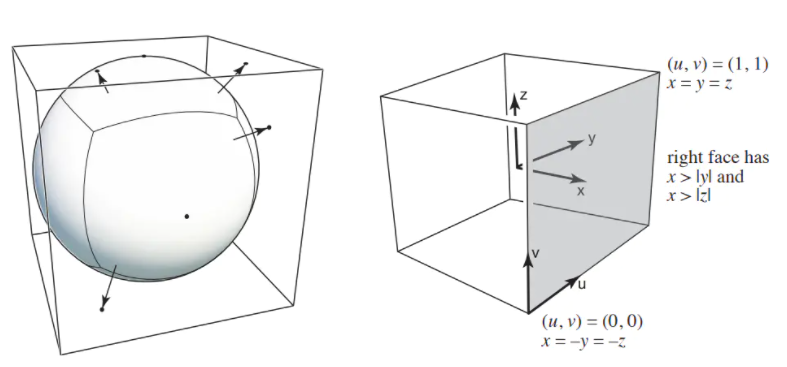
 凹凸贴图

之前我们用纹理是为了替换Blinn-Phong模型里的参数kd，除此之外，纹理还可以定义任何属性。比如它可以定义在一个模型上的点的相对高度。一个球假设它原本有一个基础的表面，然后纹理可以定义这个表面上的点沿着法线方向的相对高度。

Bump Maps

Bump Maps存储的是该点逻辑上的相对高度(可为负值)，该高度的变化实际上表现了物体表面凹凸不平的特质，利用该高度信息，再计算出该点法线向量，最后再利用该法线计算光照.

Displacement Maps

Bump Maps是逻辑上的高度改变，而Displacement Maps则是物理上的高度改变，二者的区别就在此处，可以通过物体阴影的边缘发现这点：

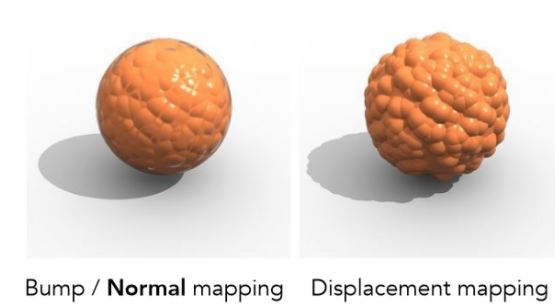
阴影贴图Shadow Maps

1.把光源当做一个摄像机让它去看，去渲染整个场景一遍从而得到从光源视角的深度Buffer，记为d

2.从设定好的摄像机位置去真正的渲染场景得到摄像机视角的深度Buffer，记为d1

3.将所有摄像机视角可见点，利用光源视角下的那一套投影矩阵，重新投影回光源，找到与之对应的深度d,如果该点在d上的深度值与d dd上的深度值相等，则说明此点可被光源与摄像机共同看见，因此不在阴影中。

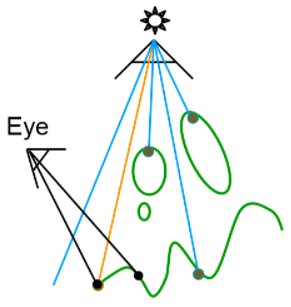
如果该点在d上的深度值小于d1上的深度值，则说明此点不可被光源看见，但摄像机看得见，即该点前方有物体遮挡，因此在阴影中，如下图这种情况

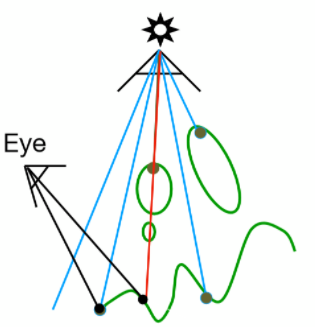
 如此便能确定每个可见像素点是否在阴影之中了，如果在阴影之中就不去计算Blinn-Phong中的镜面反射项与漫反射项

软硬阴影

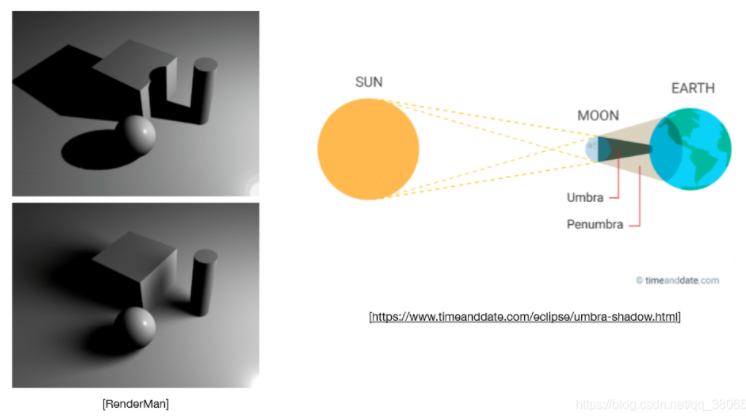
 产生这种问题的原因是因为光源具有体积，导致，有的地方完全看不到光源(本影, Umbra), 有的地方能看到一部分光源(半影，Penumbra)。所以阴影的边缘会有过渡的情况，从而产生软阴影现象，就像上图中太阳与地球的示意一样(全日食与半日食)

二、几何

几何分为隐式几何（Implicit geometry）和显式几何（Explicit geometry）。

隐式几何表示方法不会表达明确的点的位置，而是去表达这些点满足的关系，判断一个点与表面的关系非常容易，只需要将点代入到函数中，根据结果的正负值即可判断该点在表面内、在表面上还是在表面外。

用数学公式去表示表面,

另外一种表示方法是CSG (Constructive Solid Geometry, Implicit) 表示方法，它是通过基本几何的基本运算来定义新的几何，例如一个圆柱和球，做布尔运算，通过几何之间的求交集、叉积和并集就能得到新的较复杂的几何

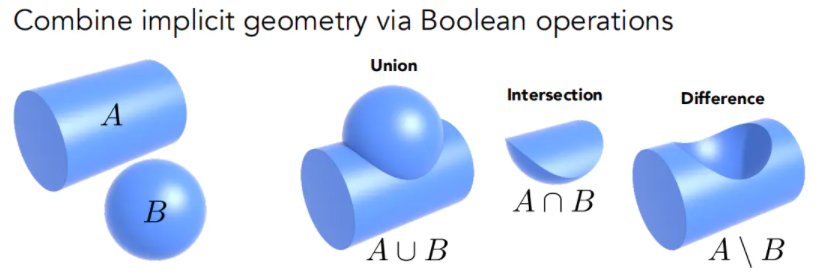
 还有一种表示方法叫距离函数 (Distance Functions, Implicit) 表示方法。对于任何一个几何，我们不去描述它的表面，而是去描述空间中的点到这个表面的最近距离。

水平集方法(Level Set Methods, Implicit)，即等高线。它就是为了描述一个函数在不同的位置有相同的值。

分形（Fractals）分形就是自相似的意思，即自己的一个部分和整体非常相似，在计算中和递归一个道理。例如雪花如果放大看会发现每一个六边形边都会有更小的六边形，即不断地自我重复所形成的形状。

接着总结一下隐式表达的优劣。好处有：描述容易（比如用一个函数），有利存储；有利查询（判断位置关系）；利于做光线求交（当然对显式来说也并不难）；对于简单的物体可以严格地描述出来，没有采样误差；容易控制拓扑变化等。坏处就是难以描述复杂形状的几何。这也是为什么我们还需要显式的表达。

显式表达也有很多种方法，例如三角形表达、贝塞尔曲面、细分曲面、NURBS、点云等。

一种特定的文件格式，这一种文件可以存储一个物体或一个场景，这种文件称为The Wavefront Object File (.obj)，注意这里的文件虽然后缀是.obj但是和编译时生成的.obj文件不是一回事。它其实是一个文本文件，这个文本文件里，只是把空间中的顶点坐标、法线、纹理坐标分开表示，然后再把它们组织起来。

三、曲线

贝塞尔曲线

贝塞尔曲线的目的是用一系列控制点去定义某一条曲线，

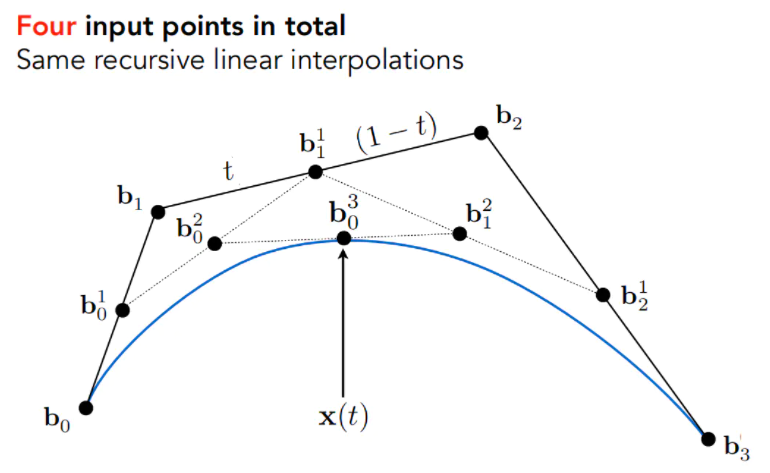
 总结归纳，给定n+1个控制点，我们可以得到一个 阶的贝塞尔曲线，它在任意时间t都是给定控制点的线性组合，它组合的系数是一个跟时间有关的多项式，这个多项式叫做Bernstein多项式

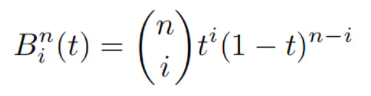
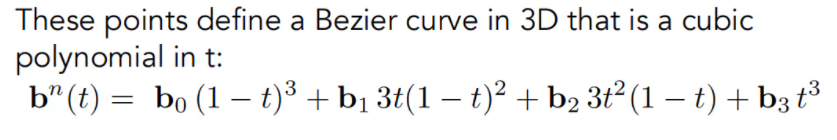
贝塞尔曲线有很多不错的性质：

1. 规定了起点和终点
2. 对于三次贝塞尔曲线（Cubic Bezier），它的起始位置的切线一定是3(b1-b0)，终点位置的切线为 ，如果控制点数不是4，那么系数就不是3了。
3. 仿射变换下有一个好性质，如果要对一条贝塞尔曲线做仿射变换，只需要对它的控制点做仿射变换，再重新绘制出来即可。因此不需要把曲线上每个点的位置都记录下来。但是对于投影变换就不行了。
4. 凸包性质，凸包是计算几何的中的概念，该性质是说，贝塞尔曲线上的任何一个点一定在几个控制点形成的凸包内，例如四个点形成了一个四边形，那么画出来的曲线一定在这个四边形内。

逐段的贝塞尔曲线（Piecewise Bezier Curves）

当控制点多的时候，这个曲线不容易控制，就得不到想要的形状。我们可以不用这么多控制点来定义一条贝塞尔曲线，可以使用多段贝塞尔曲线来定义，这样每次只用很少的控制点，最后再连起来

样条曲线

 曲面

曲面会比曲线稍微复杂一些，但是相对更好理解。首先，我们把曲线的概念延伸到一个平面上

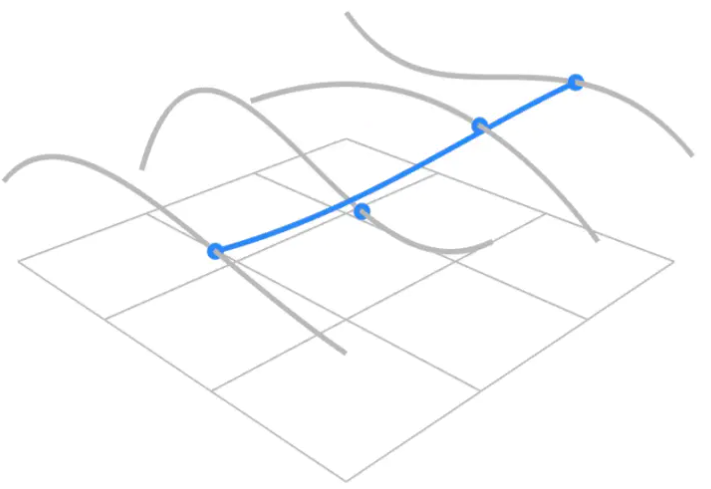
对于下图所示的曲面，可以理解成由一个平面，施加一个向上的力，拖拽上去得到的结果，它是由个控制点得到的，图中的黑点可以理解为拖拽时施加力的作用点。

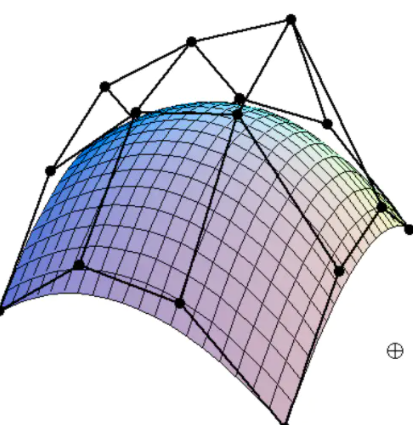
 首先在平面上定义个控制点，它有行列，先从行来看，这四根曲线上的点在不同的时间有不同的位置如果我们把这四个曲线上的控制点，认为是另外一个方向的贝塞尔曲线的控制点，我们就可以画出这条贝塞尔曲线，在这根线不断地扫掠地过程中就可以得到一个曲面。通过这种方式我们可以定义非常复杂的曲面。

用三角形来描述模型，那我们就需要了解一些关于网格的操作，例如 Subdivision （用更多的三角形来得到更光滑的模型），Simplification（减少网格面，以节省存储量），Regularization（使三角形都接近于正三角形）。

Catmull-Clark Subdivision (General Mesh)

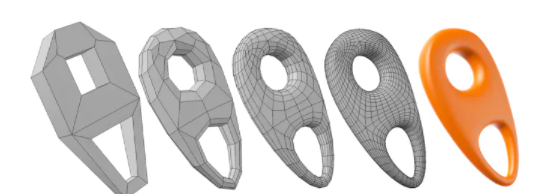
因为Loop细分只能对三角形网格进行操作，下图网格中既有三角形又有四边形的一般网格情况，就需要使用Catmull-Clark细分。

我们称Quad face为四边形面，而非四边形面当然就是Non-quad face，例如图中的两个三角形面。接着我们定义，顶点的度不为4的为奇异点

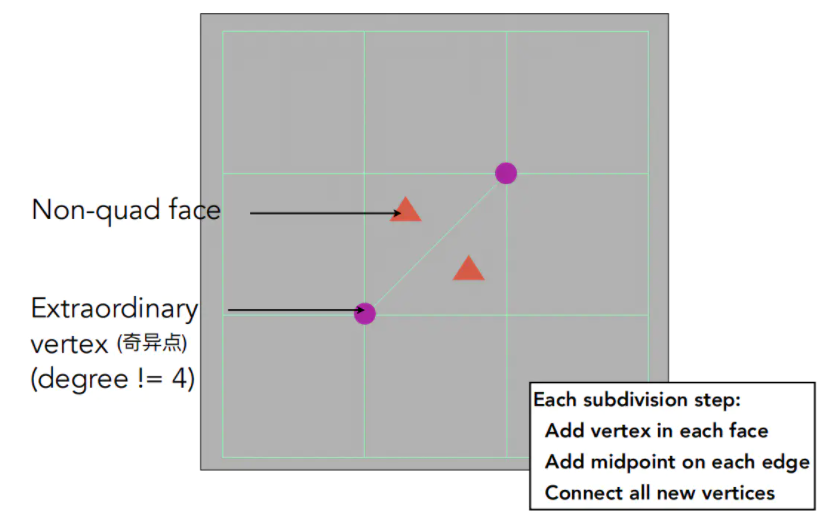
 在每一条边取中点，也在每一张面上取中点，并且把边上的中点和面上的中点连起来，这样左上角的一个四变形变成了四个四边形，三角形就细分成了三个四边形。

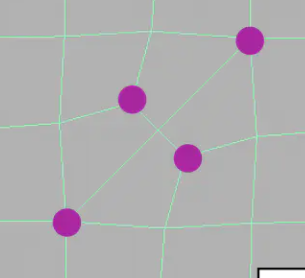
 这样的细分会在每一个非四边形面上引入一个奇异点，并且会将这些非四边形面转换为四边形面。Catmull-Clark Subdivision会在第一次细分后，增加了非四边形面的数量个奇异点，之后不再增加。

Loop细分只能用于三角形面，Catmull-Clark可以用于各种不同的面。

最后

以上就是昏睡老鼠为你收集整理的GAMES101笔记（二）一、 纹理映射二、几何三、曲线的全部内容，希望文章能够帮你解决GAMES101笔记（二）一、 纹理映射二、几何三、曲线所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。