差分的专题

69 阅读 0 评论 46 点赞

我是靠谱客的博主真实冷风，最近开发中收集的这篇文章主要介绍差分的专题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

差分性质：

例题1：

AcWing100. 增减序列

思路：

例题2：HDU-1556---Color the ball

思路：

AC代码：

差分性质：

1、差分序列求前缀和可得原序列

2、将原序列区间[L,R]中的元素全部+1，可以转化操作为差分序列L处+1，R+1处-1

3、按照性质2得到，每次修改原序列一个区间+1，那么每次差分序列修改处增加的和减少的相同

例题1：

AcWing100. 增减序列

链接：https://www.acwing.com/problem/content/102/

题目：

给定一个长度为 nn 的数列 a1,a2,…,ana1,a2,…,an，每次可以选择一个区间 [l,r]，使下标在这个区间内的数都加一或者都减一。

求至少需要多少次操作才能使数列中的所有数都一样，并求出在保证最少次数的前提下，最终得到的数列可能有多少种。

输入格式：

第一行输入正整数 n。

接下来 n 行，每行输入一个整数，第 i+1行的整数代表 ai。

输出格式：

第一行输出最少操作次数。

第二行输出最终能得到多少种结果。

数据范围：

0<n≤1e5,
0≤ai<2147483648

输入样例：

输出样例：

1
2

思路：（可以去看Y总的视频讲解）

结论：某个数组是它的差分数组的前缀和数组。所以求出已给数组a的差分数组，再让差分数组中的所有数尽可能为0，pos为差分数组所有正数的和，neg为差分数组所有负数的绝对值的和，将该数组变为全部相同的数的最小操作数为min(pos,neg)+abs(pos-neg);可以配对的正负数的值，加上差值。

AC代码：（y总的源代码）

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
const int N=100010;
int a[N];
int main(){
	int n;
	cin>>n;	
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=n;i>1;i--) a[i]-=a[i-1];//差分数组
	
	ll pos=0,neg=0;
	for(int i=2;i<=n;i++)
	   if(a[i]>0) pos+=	a[i];
	   else neg-=a[i];
	   
    cout<<min(pos,neg)+abs(pos-neg)<<endl;
    cout<<abs(pos-neg)+1<<endl;
    return 0;
}

例题2：差分入门级简单题（HDU-1556---Color the ball）

链接：https://acm.hdu.edu.cn/showproblem.php?pid=1556

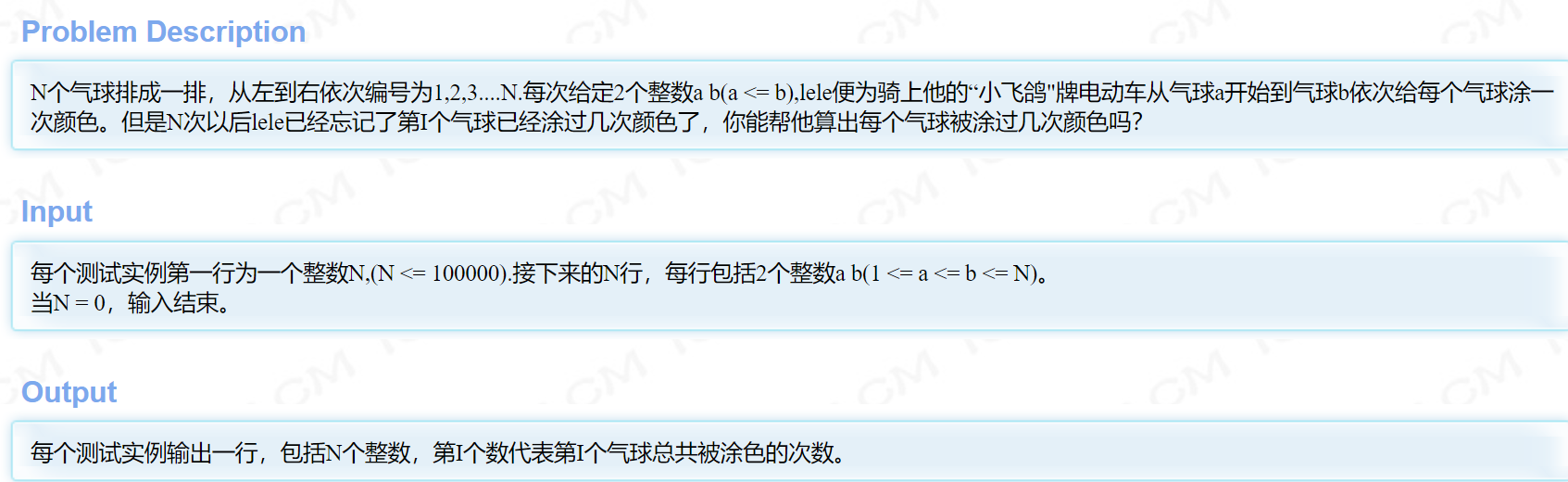
Problem Description：

N个气球排成一排，从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了，你能帮他算出每个气球被涂过几次颜色吗？

Input：

每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行，每行包括2个整数a b(1 <= a <= b <= N)。
当N = 0，输入结束。

Output：

每个测试实例输出一行，包括N个整数，第I个数代表第I个气球总共被涂色的次数。

思路：

差分入门题，直接用差分数组写就可以过。

AC代码：

#include <iostream>
#include <cstring>
using namespace std;

typedef long long ll;
const int N=100010;
int arr[N];
int main(){
    int t,left,right;
    while(cin>>t){
        int n=t;
        if(t==0) break;
        memset(arr,0,sizeof(arr));
        while(t--){
            cin>>left>>right;
            arr[left-1]++;
            arr[right]--;
        }
        cout<<arr[0];//cout<<arr[0]<<endl<<arr[1]<<endl<<arr[2]<<endl;
        for(int i=1;i<n;i++){
            arr[i]=arr[i]+arr[i-1];
            cout<<" "<<arr[i];
        } 
        cout<<endl;
    }
    return 0;
}