【问题思考总结】一个大于0的数乘以无穷大一定是无穷大吗？【关于定点和动点，数和函数，定区间和变区间的辨析】问题函数和数延伸思考：拉格朗日中值定理在定区间和变区间和无穷区间上的辨析

问题

在看一道题的解析的时候，发现了这个问题，就是$f^{\prime }(c)(n-2)$当n趋于无穷且$f^{\prime }(c)>0$的时候，为什么取值是无穷？我的想法是：这个一阶导数虽然大于0，但是他的极限等于0呢？0乘以无穷不是不一定是无穷吗？还可能是0呢！
基于这个问题，我们开始讨论。

函数和数

首先看刚才的论断，里面有一句说，极限等于0乘以无穷不一定是无穷。
这句话显然是没有问题的，不过，极限等于0的数，还有一个说法，叫做无穷小。

无穷小实际上是一个变量，指的是极限等于0的函数或者数列，指的是，你任意取一个多么小的数，我总可以通过逼近$x_0(li{m}_{x->x_0}=0)$的方法，来比你更小。

回到刚才的论断里，题目里的$f(c)$这个$c$实际上是一个有限区间上的一个中值，因此是一个确定的值。这个我的理解是，定区间上，函数性态是确定的（埋下一个伏笔），因此能够确定一个定点。

那么因为这是一个定点，那么由函数的映射关系可知，唯一对应一个函数值。因此，函数值是常数。仿照无穷小的定义，无穷大的定义则是总有一个数比你更大。那么一个有限的，且不为0的数，不管你是多少，你都是一个数，我是函数，无穷，我的力量你不会了解。因此，这个常数乘以无穷大还是无穷大。

至此，我们知道了之前的问题在于混淆了函数和数的概念。

总结一下：

1. 无穷小是个函数
2. 正（负）数乘以无穷，结果是正（负）无穷，0乘以无穷是0。

也就是答案的方法是正确的。然而，随着问题的深入，我又想到了一个问题：这个是用中值定理证明的，中值是$\xi$，他会不会是一个变量呢？

延伸思考：拉格朗日中值定理在定区间和变区间和无穷区间上的辨析

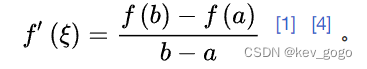
就像之前提到的一样，这个在定区间上，实际上就是这个函数性态是确定的，因此这个导数值等于公式右边的函数值之差除以自变量之差的点$\xi$也是确定的。

因此，这个定区间上的中值点是个定点（可能是很多个点，但是每个点都是定点）

在变区间上，想象这样一个区间$[n-1,n]$实际上，公式的右侧，分子分母都是变量相加减，因此是个变区间，那么在变区间上，这个函数的性态其实是不一定的，因为你不知道他究竟在哪一段加粗样式，因此在变区间上使用拉格朗日中值定理一定要小心（也有在变区间可以使用的情况，比如将区间取极限之类的操作变成定区间），这个中值是一个和区间的两侧的变量取值紧密相关的。

最后，在无穷区间上是不能使用拉格朗日中值定理的，这个证明我看了一下，大概就是用反证法来证明的，有兴趣的朋友可以看一下：拉格朗日在无穷区间上不成立的证明。

最后

以上就是魁梧煎蛋为你收集整理的【问题思考总结】一个大于0的数乘以无穷大一定是无穷大吗？【关于定点和动点，数和函数，定区间和变区间的辨析】问题函数和数延伸思考：拉格朗日中值定理在定区间和变区间和无穷区间上的辨析的全部内容，希望文章能够帮你解决【问题思考总结】一个大于0的数乘以无穷大一定是无穷大吗？【关于定点和动点，数和函数，定区间和变区间的辨析】问题函数和数延伸思考：拉格朗日中值定理在定区间和变区间和无穷区间上的辨析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。