二叉搜索树之二叉搜索树的后序遍历序列

1.本题知识点

   二叉树，递归

2. 题目描述

   输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

3. 思路

   二叉搜索树BST感觉比二叉树要简单，因为它是有规律的，二叉搜索树的左子树都比根节点要小，右子树都比根节点要大。

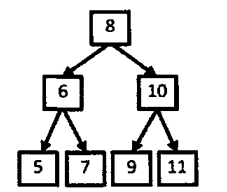
   上述二叉搜索树的后序遍历结果为：5 7 6 9 11 10 8

   Java版本：

public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
        return bst(sequence,0,sequence.length-1);
    }
    
    public boolean bst(int [] sequence,int begin,int end)
    {
        if(sequence == null || sequence.length == 0) return false;

        //1.确定根节点
        int root = sequence[end];
        int i = begin;//左子树起始索引
        //2.确定左右子树分解点，通过遍历左子树
        for(;i < end ; i++){
            //当找到第一个大于root的数值时，即找到了左右子树的分界点
            if(sequence[i] > root) break;
        }
        
        int j = i;//右子树起始索引
        //3.判断右子树符不符合二叉搜索树的特性
        for(; j < end; j++){
            //右子树中有小于root的数值，return fasle
            if(sequence[j] < root) return false;
        }
        
        //4.左右子树递归，判断左子树是不是二叉搜索树
        boolean left = true;
        if(i > begin){
            left = bst(sequence,begin, i-1);//i-1 为左子树的倒数第一个索引
        }
        //递归判断右子树是不是二叉搜索树
        boolean right = true;
        if(i < end -1 ){
            right = bst(sequence,i, end - 1);//end - 1为数组倒数第2个节点:右子树的倒数第一个索引
        }
        
        return left && right;
    }
}

最后

以上就是神勇胡萝卜为你收集整理的二叉搜索树之二叉搜索树的后序遍历序列的全部内容，希望文章能够帮你解决二叉搜索树之二叉搜索树的后序遍历序列所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。