1. 首页
  2. 文章中心
  3. 数据结构

[C语言]二叉搜索树

71 阅读 0 评论
我是靠谱客的博主 寒冷小丸子，最近开发中收集的这篇文章主要介绍[C语言]二叉搜索树，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

目录

    • 结构体
    • 二叉搜索树的插入(创建)
    • 查找值
    • 查找最小值和最大值
    • 删除单个节点
    • 遍历
    • 全部代码
    • 效果图

结构体

这个和普通的二叉树一样的

typedef struct BiTNode
{
	DataType data;    //数值 
	struct BiTNode* lchild;  //左孩子 
	struct BiTNode* rchild;  //右孩子 
	int flag;  //非递归遍历时可能会使用到
} BiTNode,*BiTree; //搜索树结构体

二叉搜索树的插入(创建)

这个相当于创建了一棵二叉搜索树
我使用了递归和迭代两种方法,迭代效率更高些,不过更臃肿些

//递归插入并返回头节点
BiTree Insert_D(BiTree root, DataType data)
{
	if(!root)//找到了对应位置 那就插入(就是让这个空节点变成插入的这个节点)! 
	{
		root = (BiTree)malloc(sizeof(BiTNode));
		root->data = data;
		root->flag = 0;
		root->lchild = root->rchild = NULL;
	}
	else//没找到就继续找 
	{
		if(data < root->data)
			root->lchild = Insert_D(root->lchild,data);//往后面找 
		else
			root->rchild = Insert_D(root->rchild,data);
	}
	return root;//返回这一层的头节点指针 
}

//迭代插入并返回头节点
BiTree Insert(BiTree root, DataType data)
{
	BiTree Faceroot,Preroot;  //保存头节点
	Faceroot = root; //指向前一个节点
	while(root)//找到对应位置
	{
		Preroot = root;
		if(data < root->data)
			root = root->lchild;
		else
			root = root->rchild;
	}
	
	root = (BiTree)malloc(sizeof(BiTNode));//给要插入的数值创建空间 
	root->data = data;
	root->flag = 0;
	root->lchild = root->rchild = NULL;
	
	if(!Faceroot)   //用于给空树插入时返回第一个插入的节点的指针 
		return root;
	if(data < Preroot->data)//给Preroot后面插入新创建节点 
		Preroot->lchild = root;
	else
		Preroot->rchild = root;
	return Faceroot; //返回树的头节点指针
}

查找值

这里也是使用了递归和迭代,个人感觉这个的迭代更好写一些

//尾递归查找
//从root节点开始往下查找 关键值key,如果找到就返回key节点的指针,否则返回NULL
BiTree Find_D(BiTree root,DataType key)
{
	if(!root)
		return NULL;
	if(key < root->data)
		return Find_D(root->lchild,key);
	else if(key > root->data)
		return Find_D(root->rchild,key);
	else
		return root;
}

//迭代查找
//从root节点开始往下查找 关键值key,如果找到就返回key节点的指针,否则返回NULL
BiTree Find(BiTree root,DataType key)
{
	while(root)
	{
		if(root->data == key)
			break;
		else if(key < root->data)
			root = root->lchild;
		else
			root = root->rchild;
	}
	return root;
}

查找最小值和最大值

这里也是两种方法,差别也不大

//从root节点开始迭代查找最小值,找到就返回其指向该节点指针,否则返回NULL
BiTree FindMin(BiTree root)//最左边
{
	if(root)
		while(root->lchild)
			root=root->lchild;
	return root;
}

//从root节点开始迭代查找最大值,找到就返回其指向该节点指针,否则返回NULL
BiTree FindMax(BiTree root)//最右边 
{
	if(root)
		while(root->rchild)
			root=root->rchild;
	return root;
}

//递归查找最大值
BiTree FindMax_D(BiTree root)
{
	if(!root)
		return NULL;
	if(!root->rchild)
		return root;
	return FindMax_D(root->rchild);
}

删除单个节点

这个就需要慢慢来理解一下了(手绘了一下,有亿点点丑…)

删除节点大概三种方案
第一种:
在这里插入图片描述
第二种:
在这里插入图片描述
第三种:
在这里插入图片描述

//删除节点
BiTree Del(BiTree root, DataType key)
{
	if(root)
	{
		if(key < root->data)
			root->lchild = Del(root->lchild,key);
		else if(key > root->data)
			root->rchild = Del(root->rchild,key);
		else  //找到要删除的点啦 
		{
			if(root->lchild&&root->rchild)//两个孩子都存在的情况
			{
				BiTree temp = FindMin(root->rchild);  //寻找右孩子里的最小值 (ps:也可以左孩子里最大值) 然后让需要被删除的点的值变成那个最小值(或者最大值),然后去删除那个最小值...递归 
				root->data = temp->data;
				root->rchild = Del(root->rchild,root->data);
			}
			else //叶子节点或者只有一个孩子的情况 
			{
				BiTree temp = root;
				if(root->lchild) 	//有左孩子就让它等于左孩子节点
					root = root->lchild;
				else if(root->rchild)	//有右孩子就让它等于右孩子节点
					root = root->rchild;
				else	//如果是叶子节点就让它为空
					root = NULL;
				free(temp);
			}
		}
	}
	else
		printf("没有该节点n");
	return root;//返回节点
}

遍历

//先序遍历 
void ProPrint(BiTree root)//这个的先序遍历和最开始输入的顺序是一样的,其他遍历方式可以参考之前写的文章
{
	if(!root)
		return;
	printf("%d ",root->data);
	ProPrint(root->lchild);
	ProPrint(root->rchild);
}

全部代码

注意:二叉搜索树的中序遍历是有序的

#include<stdio.h>
#include<stdlib.h>
typedef int DataType;  //自定义节点数值类型 

typedef struct BiTNode
{
	DataType data;    //数值 
	struct BiTNode* lchild;  //左孩子 
	struct BiTNode* rchild;  //右孩子 
	int flag;
} BiTNode,*BiTree;//搜索树结构体 

//尾递归查找
//从root节点开始往下查找 关键值key,如果找到就返回key节点的指针,否则返回NULL
BiTree Find_D(BiTree root,DataType key)
{
	if(!root)
		return NULL;
	if(key < root->data)
		return Find_D(root->lchild,key);
	else if(key > root->data)
		return Find_D(root->rchild,key);
	else
		return root;
}

//迭代查找
//从root节点开始往下查找 关键值key,如果找到就返回key节点的指针,否则返回NULL
BiTree Find(BiTree root,DataType key)
{
	while(root)
	{
		if(root->data == key)
			break;
		else if(key < root->data)
			root = root->lchild;
		else
			root = root->rchild;
	}
	return root;
}

//从root节点开始迭代查找最小值,找到就返回其指向该节点指针,否则返回NULL
BiTree FindMin(BiTree root)//最左边
{
	if(root)
		while(root->lchild)
			root=root->lchild;
	return root;
}

//从root节点开始迭代查找最大值,找到就返回其指向该节点指针,否则返回NULL
BiTree FindMax(BiTree root)//最右边 
{
	if(root)
		while(root->rchild)
			root=root->rchild;
	return root;
}

//递归查找最大值
BiTree FindMax_D(BiTree root)
{
	if(!root)
		return NULL;
	if(!root->rchild)
		return root;
	return FindMax_D(root->rchild);
}

//递归插入并返回头节点
BiTree Insert_D(BiTree root, DataType data)
{
	if(!root)//找到了对应位置 那就插入(就是让这个空节点变成插入的这个节点)! 
	{
		root = (BiTree)malloc(sizeof(BiTNode));
		root->data = data;
		root->flag = 0;
		root->lchild = root->rchild = NULL;
	}
	else//没找到就继续找 
	{
		if(data < root->data)
			root->lchild = Insert_D(root->lchild,data);//往后面找 
		else
			root->rchild = Insert_D(root->rchild,data);
	}
	return root;//返回这一层的头节点指针 
}

//迭代插入并返回头节点
BiTree Insert(BiTree root, DataType data)
{
	BiTree Faceroot,Preroot;  //保存头节点
	Faceroot = root; //指向前一个节点
	while(root)//找到对应位置
	{
		Preroot = root;
		if(data < root->data)
			root = root->lchild;
		else
			root = root->rchild;
	}
	
	root = (BiTree)malloc(sizeof(BiTNode));//给要插入的数值创建空间 
	root->data = data;
	root->flag = 0;
	root->lchild = root->rchild = NULL;
	
	if(!Faceroot)   //用于给空树插入时返回第一个插入的节点的指针 
		return root;
	if(data < Preroot->data)//给Preroot后面插入新创建节点 
		Preroot->lchild = root;
	else
		Preroot->rchild = root;
	return Faceroot; //返回树的头节点指针
}

//删除节点
BiTree Del(BiTree root, DataType key)
{
	if(root)
	{
		if(key < root->data)
			root->lchild = Del(root->lchild,key);
		else if(key > root->data)
			root->rchild = Del(root->rchild,key);
		else  //找到要删除的点啦 
		{
			if(root->lchild&&root->rchild)//两个孩子都存在的情况
			{
				BiTree temp = FindMin(root->rchild);  //寻找右孩子里的最小值 (ps:也可以左孩子里最大值) 然后让需要被删除的点的值变成那个最小值(或者最大值),然后去删除那个最小值...递归 
				root->data = temp->data;
				root->rchild = Del(root->rchild,root->data);
			}
			else //叶子节点或者只有一个孩子的情况 
			{
				BiTree temp = root;
				if(root->lchild) 	//有左孩子就让它等于左孩子节点
					root = root->lchild;
				else if(root->rchild)	//有右孩子就让它等于右孩子节点
					root = root->rchild;
				else	//如果是叶子节点就让它为空
					root = NULL;
				free(temp);
			}
		}
	}
	else
		printf("没有该节点n");
	return root;//返回节点
}

//先序遍历 
void ProPrint(BiTree root)
{
	if(!root)
		return;
	printf("%d ",root->data);
	ProPrint(root->lchild);
	ProPrint(root->rchild);
}

int main()
{
	BiTree root = NULL;
	printf("请输入数值来建立二叉搜索树,q停止输入:");
	DataType data;
	while(scanf("%d",&data)==1)
		root = Insert(root,data);
	printf("二叉搜索树的先序遍历为:");
	ProPrint(root);
	putchar('n');
	BiTree p;
	p = FindMax(root);
	if(p)
		printf("最大值为:%dn",p->data);
	p = FindMin(root);
	if(p)
		printf("最小值为:%dn",p->data);
	fflush(stdin);
	printf("请输入需要删除的节点的值:");
	scanf("%d",&data);
	Del(root,data);
	printf("二叉搜索树的先序遍历为:");//这个和输入的顺序是一样的... 
	ProPrint(root);
	return 0;
}

效果图

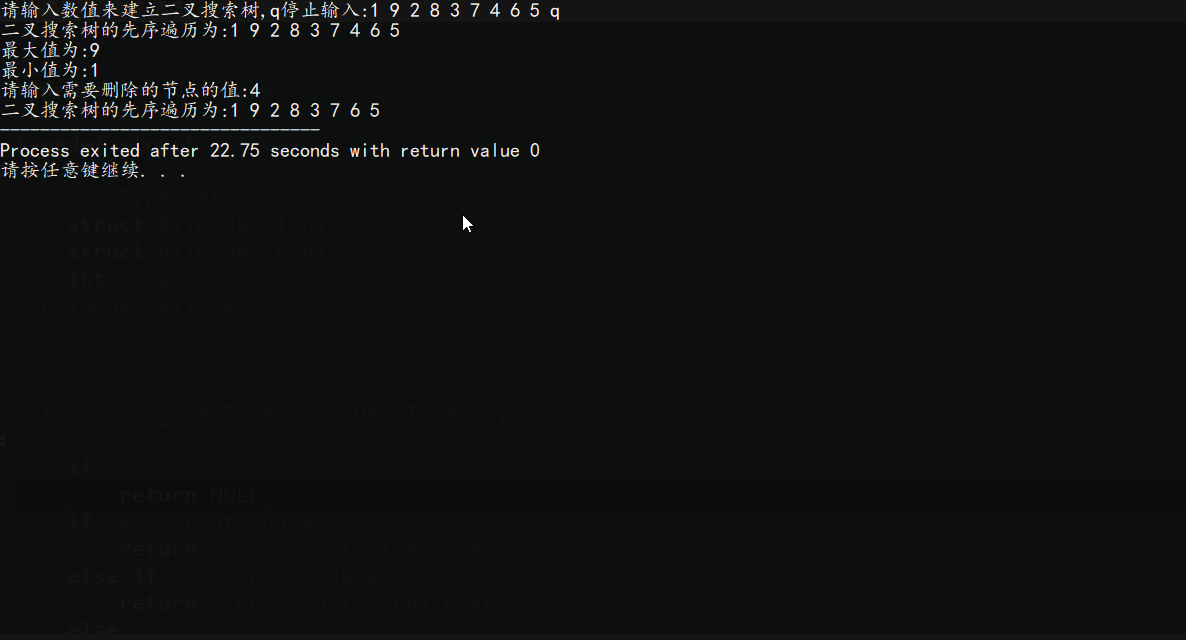
在这里插入图片描述
可能会有一些地方写的不好或者有错误,如果有建议请您指出,我一定洗耳恭听,谢谢

最后

以上就是寒冷小丸子为你收集整理的[C语言]二叉搜索树的全部内容，希望文章能够帮你解决[C语言]二叉搜索树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(47)

相关文章

python实现二叉查找数的查找最小值、最大值操作
python实现二叉查找数的查找最小值、最大值操作
JZ54 二叉搜索树的第k个节点
JZ54 二叉搜索树的第k个节点
530.二叉搜索树的最小绝对差递归
530.二叉搜索树的最小绝对差递归
15.5 最优二叉搜索树（笔记）背景定义相关公式相关算法
15.5 最优二叉搜索树（笔记）背景定义相关公式相关算法
[C语言]二叉搜索树
[C语言]二叉搜索树
最优二叉查找树
最优二叉查找树
二叉树的后序遍历相关题目
二叉树的后序遍历相关题目
二叉搜索树之二叉搜索树的后序遍历序列
二叉搜索树之二叉搜索树的后序遍历序列

评论列表共有 0 条评论

立即
投稿
返回
顶部