概述
X.遍历二叉树的方法合集
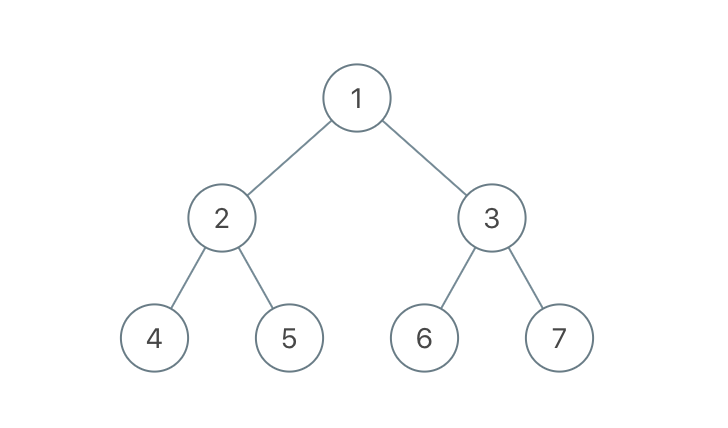
关于 LeetCode 上的3道题的解法
-
- 二叉树的中序遍历
-
- 二叉树的前序遍历
-
- 二叉树的后序遍历
只要参考任意一种解法的代码，将其中的输出代码替换成添加数组元素即可。
在文章的最后给出了 144. 二叉树的前序遍历 的答案。
我的本意是想让大家能深入的理解二叉树遍历的过程，之后完成这三道题和其它二叉树遍历的题目能够感觉轻松一点。
文章有一点长，代码居多。会给出比较详细的动画演示以及视频讲解请大家耐心阅读。
递归解法
这里直接给出递归遍历的3中常用解法。
前中后序的简单动画
前序遍历
代码片段
public static void preOrderRecur(TreeNode head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
中序遍历
代码片段
public static void preOrderRecur(TreeNode head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
后序遍历
代码片段
public static void postOrderRecur(TreeNode head) {
if (head == null) {
return;
}
postOrderRecur(head.left);
postOrderRecur(head.right);
System.out.print(head.value + " ");
}
代码解释
这里没有对递归遍历做过多的解释，仅仅给出了简单的动画演示。
要理解递归的思路并且熟练的使用它，就是要 想清楚你想做什么，什么时候停止。
如前序遍历：
我想先打印头节点对吧？那我打印完了头节点，我现在想打印左边节点了，我只是告诉计算机我想打印左边结点，之后打印右边结点。
那么后序遍历呢？
这个时候你应该知道了，我就是想操作左边然后右边，最后打印中间的元素。
我们并不需要太过于在意具体的递归过程，而是要想清楚让计算机干什么。
计算机都可能溢出，用人脑去遍历就不现实了吧，看开点。
迭代解法
本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用Stack来模拟系统栈。
前序遍历
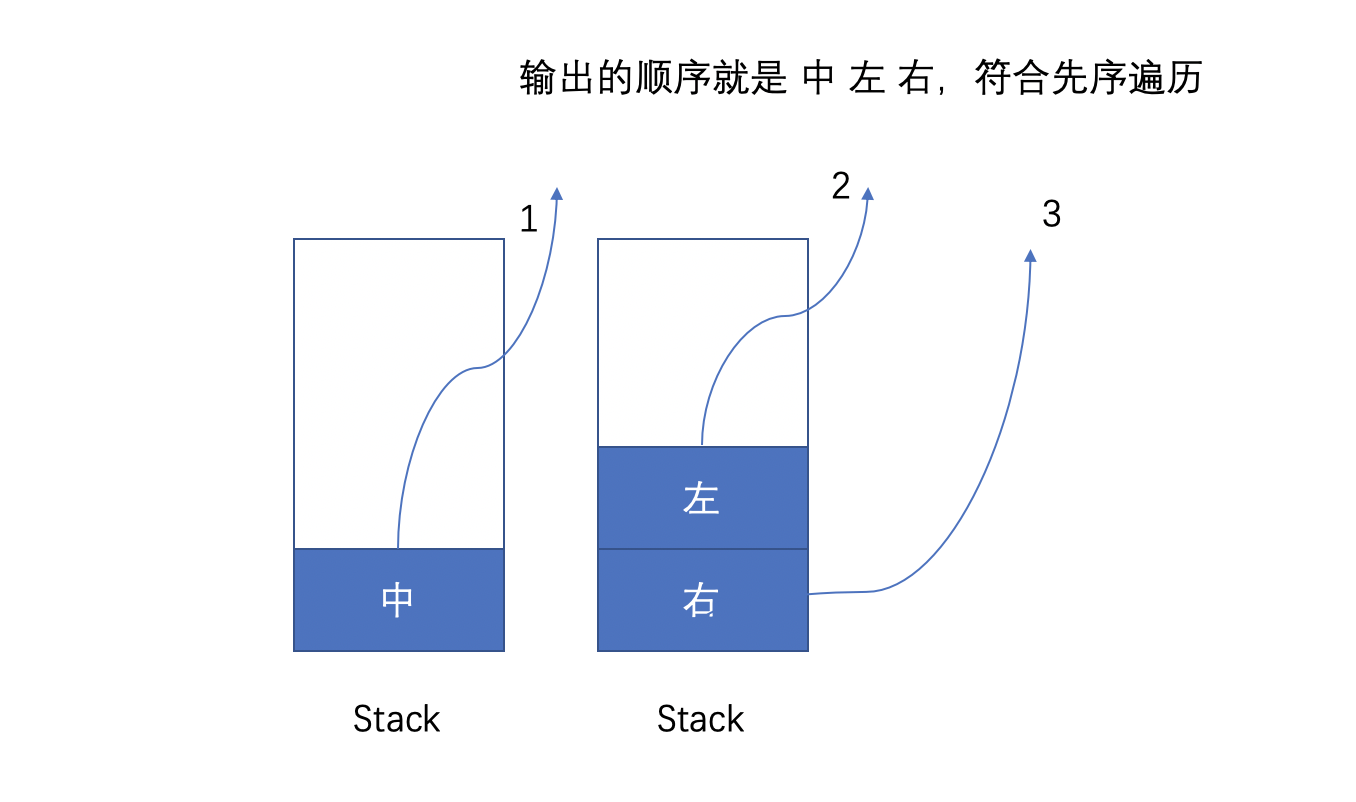
首先我们应该创建一个Stack用来存放节点，首先我们想要打印根节点的数据，此时Stack里面的内容为空，所以我们优先将头结点加入Stack，然后打印。
之后我们应该先打印左子树，然后右子树。所以先加入Stack的就是右子树，然后左子树。
此时你能得到的流程如下:
代码片段
public static void preOrderIteration(TreeNode head) {
if (head == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
System.out.print(node.value + " ");
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
中序遍历
- 同理创建一个
Stack，然后按 左 中 右的顺序输出节点。 - 尽可能的将这个节点的左子树压入
Stack，此时栈顶的元素是最左侧的元素，其目的是找到一个最小单位的子树(也就是最左侧的一个节点)，并且在寻找的过程中记录了来源，才能返回上层,同时在返回上层的时候已经处理完毕左子树了。。 - 当处理完最小单位的子树时，返回到上层处理了中间节点。（如果把整个左中右的遍历都理解成子树的话，就是处理完
左子树->中间(就是一个节点)->右子树） - 如果有右节点，其也要进行中序遍历。
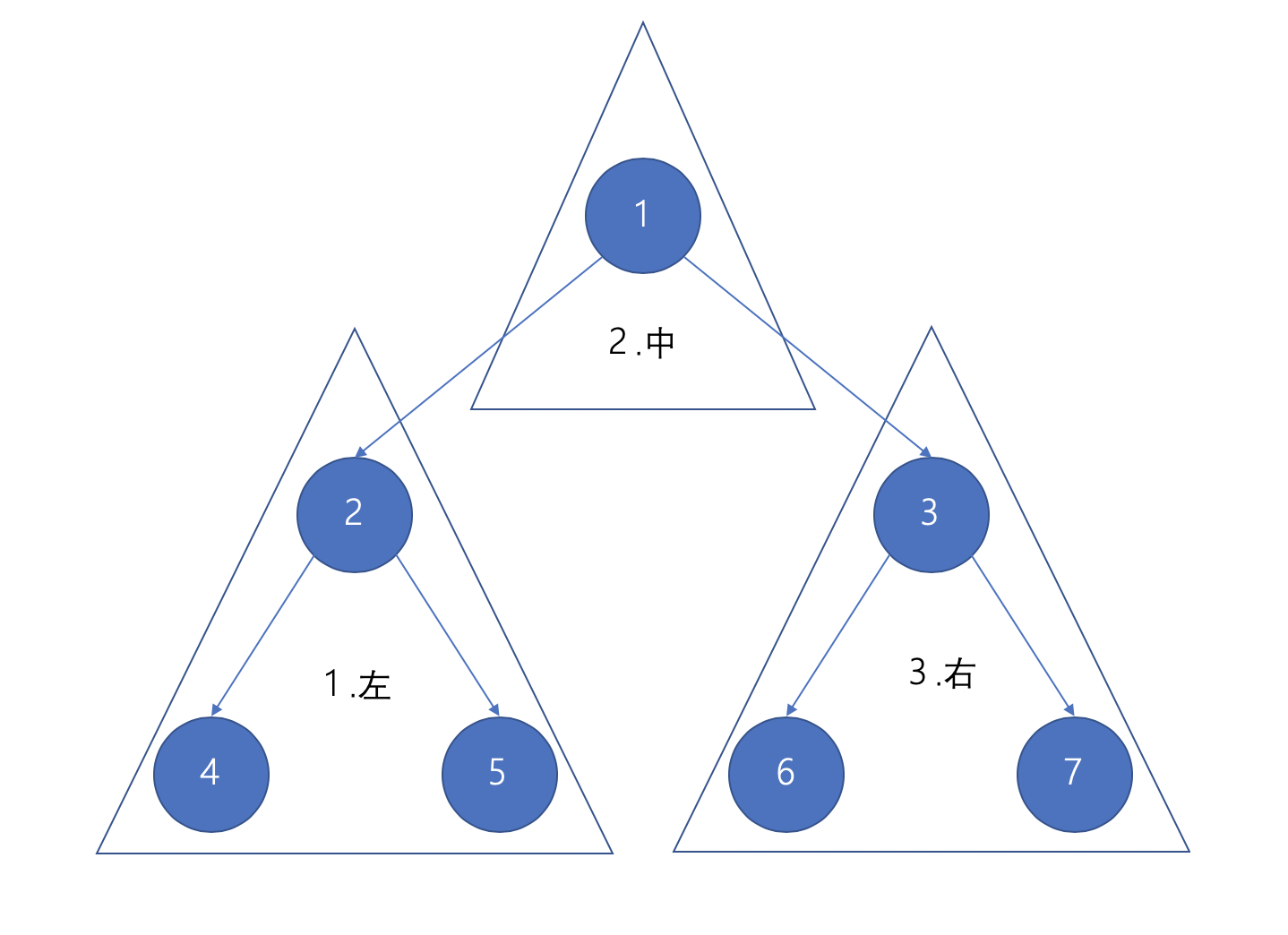
当整个左子树退栈的时候这个时候输出了该子树的根节点 2，之后输出中间节点 1。然后处理根节点为3右子树。
代码片段
public static void inOrderIteration(TreeNode head) {
if (head == null) {
return;
}
TreeNode cur = head;
Stack<TreeNode> stack = new Stack<>();
while (!stack.isEmpty() || cur != null) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode node = stack.pop();
System.out.print(node.value + " ");
if (node.right != null) {
cur = node.right;
}
}
}
后序遍历
代码片段1
- 前序遍历的过程 是 中左右。
- 将其转化成 中右左。也就是压栈的过程中优先压入左子树，在压入右子树。
- 然后将这个结果返回来，这里是利用栈的先进后出倒序打印。
public static void postOrderIteration(TreeNode head) {
if (head == null) {
return;
}
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.push(head);
while (!stack1.isEmpty()) {
TreeNode node = stack1.pop();
stack2.push(node);
if (node.left != null) {
stack1.push(node.left);
}
if (node.right != null) {
stack1.push(node.right);
}
}
while (!stack2.isEmpty()) {
System.out.print(stack2.pop().value + " ");
}
}
代码片段2
- 用一个指针
cur标记当前退出的节点是什么。 - 后序遍历的过程中在遍历完左子树跟右子树
cur都会回到根结点。所以当前不管是从左子树还是右子树回到根结点都不应该再操作了，应该退回上层。 - 如果是从右边再返回根结点，应该回到上层。
public static void postOrderIteration2(TreeNode head) {
if (head == null) {
return;
}
TreeNode cur = null;
Stack<TreeNode> stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()) {
TreeNode peek = stack.peek();
if (peek.left != null && peek.left != cur && peek.right != cur) {
stack.push(peek.left);
cur = peek.left;
} else if (peek.right != null && peek.right != cur) {
stack.push(peek.right);
cur = peek.right;
} else {
TreeNode pop = stack.pop();
System.out.print(pop.value + " ");
cur = pop;
}
}
}
Morris解法
Morris遍历使用二叉树节点中大量指向null的指针，由Joseph Morris 于1979年发明。
时间复杂度：
O
(
n
)
O(n)
O(n)
额外空间复杂度：
O
(
1
)
O(1)
O(1)
在你阅读以下代码之前，在这边先讲解一下Morris的通用解法过程。
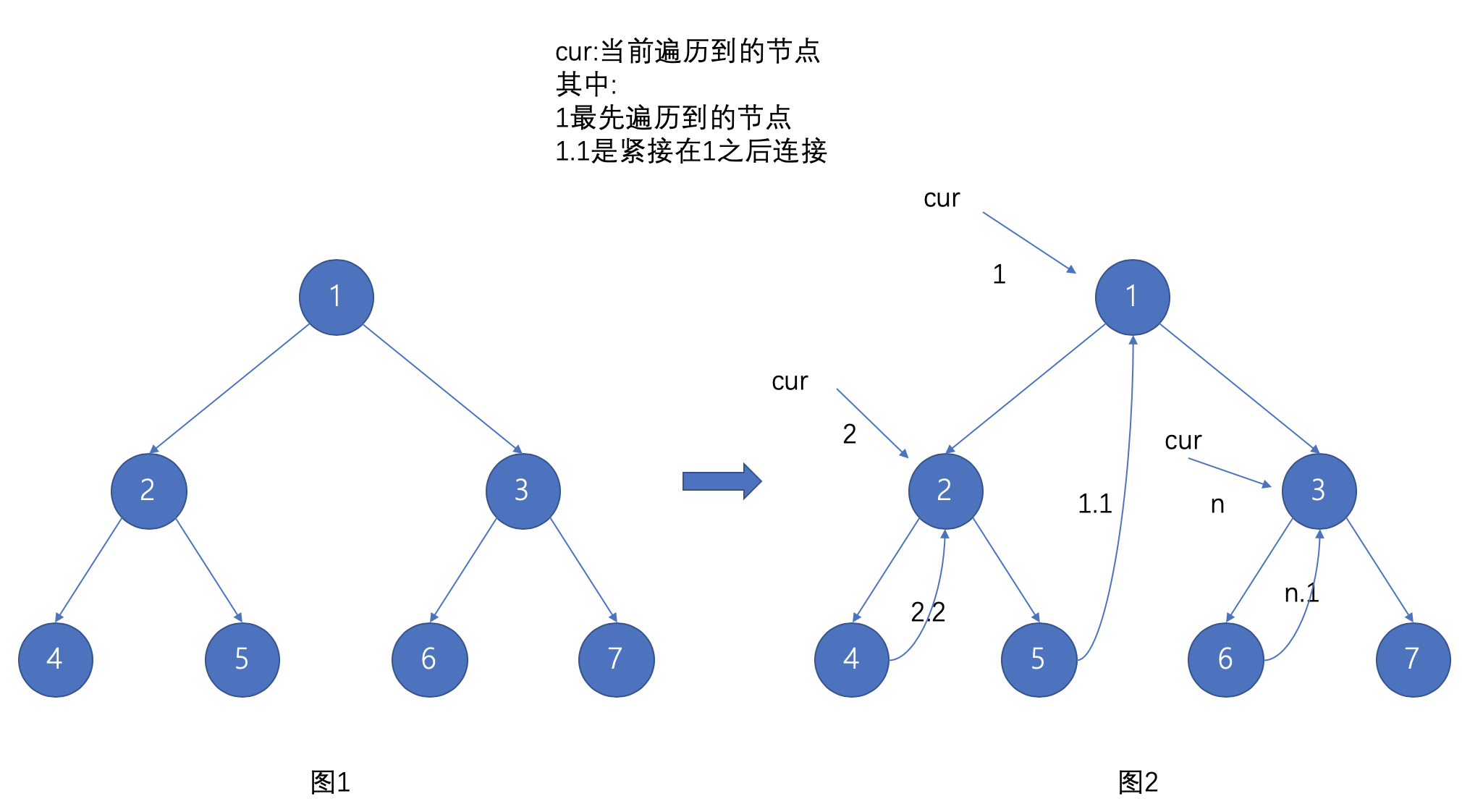
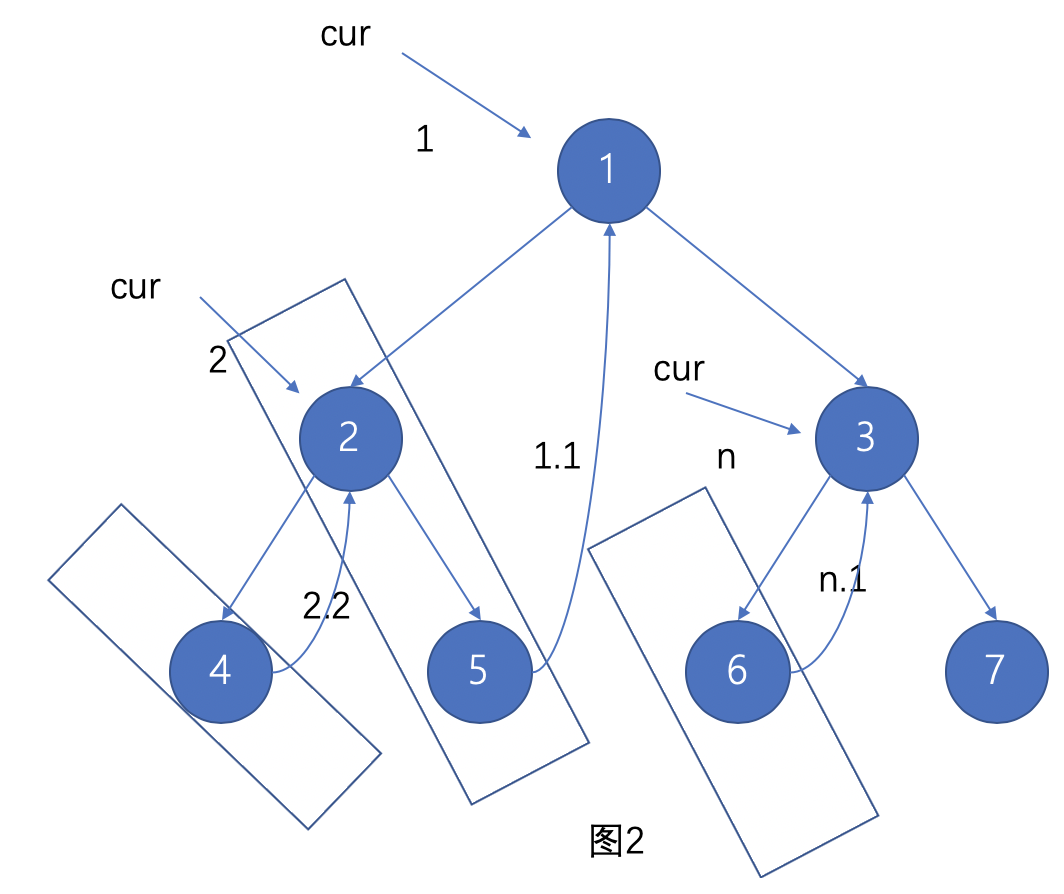
Morris的整体思路就是将 以某个根结点开始，找到它左子树的最右侧节点之后与这个根结点进行连接
我们可以从 图2 看到，如果这么连接之后，cur 这个指针是可以完整的从一个节点顺着下一个节点遍历，将整棵树遍历完毕，直到 7 这个节点右侧没有指向。
模板代码
public static void preOrderMorris(TreeNode head) {
if (head == null) {
return;
}
TreeNode cur1 = head;//当前开始遍历的节点
TreeNode cur2 = null;//记录当前结点的左子树
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {//找到当前左子树的最右侧节点，且这个节点应该在指向根结点之前，否则整个节点又回到了根结点。
cur2 = cur2.right;
}
if (cur2.right == null) {//这个时候如果最右侧这个节点的右指针没有指向根结点，创建连接然后往下一个左子树的根结点进行连接操作。
cur2.right = cur1;
cur1 = cur1.left;
continue;
} else {//当左子树的最右侧节点有指向根结点，此时说明我们已经回到了根结点并重复了之前的操作，同时在回到根结点的时候我们应该已经处理完 左子树的最右侧节点 了，把路断开。
cur2.right = null;
}
}
cur1 = cur1.right;//一直往右边走，参考图
}
}
前序遍历
- 在某个根结点创建连线的时候打印。因为我们是顺着左边的根节点来创建连线，且创建的过程只有一次。
- 打印某些自身无法创建连线的节点，也就是叶子节点。
代码片段
public static void preOrderMorris(TreeNode head) {
if (head == null) {
return;
}
TreeNode cur1 = head;
TreeNode cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
System.out.print(cur1.value + " ");
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
}
} else {
System.out.print(cur1.value + " ");
}
cur1 = cur1.right;
}
}
中序遍历
从最左侧开始顺着右节点打印。也就是在将cu1切换到上层节点的时候。
代码片段
public static void inOrderMorris(TreeNode head) {
if (head == null) {
return;
}
TreeNode cur1 = head;
TreeNode cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
//构建连接线
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
}
}
System.out.print(cur1.value + " ");
cur1 = cur1.right;
}
}
后序遍历
后序遍历就比较复杂了哈，先看一下图
当我们到达最左侧，也就是左边连线已经创建完毕了。
打印 4
打印 5 2
打印 6
打印 7 3 1
我们将一个节点的连续右节点当成一个单链表来看待。
当我们返回上层之后，也就是将连线断开的时候，打印下层的单链表。
比如返回到 ２，此时打印 ４
比如返回到 １，此时打印 ５ ２
比如返回到 ３，此时打印 ６
那么我们只需要将这个单链表逆序打印就行了，下文也给出了 单链表逆序代码
这里不应该打印当前层，而是下一层，否则根结点会先与右边打印。
代码片段
//后序Morris
public static void postOrderMorris(TreeNode head) {
if (head == null) {
return;
}
TreeNode cur1 = head;//遍历树的指针变量
TreeNode cur2 = null;//当前子树的最右节点
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
postMorrisPrint(cur1.left);
}
}
cur1 = cur1.right;
}
postMorrisPrint(head);
}
//打印函数
public static void postMorrisPrint(TreeNode head) {
TreeNode reverseList = postMorrisReverseList(head);
TreeNode cur = reverseList;
while (cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
postMorrisReverseList(reverseList);
}
//翻转单链表
public static TreeNode postMorrisReverseList(TreeNode head) {
TreeNode cur = head;
TreeNode pre = null;
while (cur != null) {
TreeNode next = cur.right;
cur.right = pre;
pre = cur;
cur = next;
}
return pre;
}
最后
以上就是完美红酒为你收集整理的【LeetCode算法修炼+动画演示】【二叉树的遍历】——X.遍历二叉树的方法合集、Morris遍历、94. 二叉树的中序遍历、144. 二叉树的前序遍历、145. 二叉树的后序遍历X.遍历二叉树的方法合集的全部内容，希望文章能够帮你解决【LeetCode算法修炼+动画演示】【二叉树的遍历】——X.遍历二叉树的方法合集、Morris遍历、94. 二叉树的中序遍历、144. 二叉树的前序遍历、145. 二叉树的后序遍历X.遍历二叉树的方法合集所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复