树——二叉树遍历

二叉树的概念：二叉树也是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：

(1)空二叉树——(a)；

(2)只有一个根结点的二叉树——(b)；

(3)右子树为空的二叉树——(c)；

(4)左子树为空的二叉树——(d)；

(5)完全二叉树——(e)   注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。

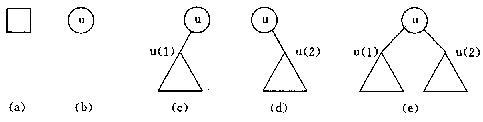
二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用作二叉查找树和二叉堆。二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2的（i-1）次方个结点；深度为k的二叉树至多有2^(k) -1个结点；对任何一棵二叉树T，如果其终端结点数(即叶子结点数)为n0，度为2的结点数为n2，则n0 = n2 + 1。

树和二叉树的2个主要差别：

　　1. 树中结点的最大度数没有限制，而二叉树结点的最大度数为2；

　　2. 树的结点无左、右之分，而二叉树的结点有左、右之分。……

　　树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。

遍历二叉树：

       所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

遍历方案

　　从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作：

　　（1）访问结点本身(N)，

　　（2）遍历该结点的左子树(L)，

　　（3）遍历该结点的右子树(R)。

　　以上三种操作有六种执行次序：

　　NLR、LNR、LRN、NRL、RNL、RLN。

　　注意：

　　前三种次序与后三种次序对称，故只讨论先左后右的前三种次序。

三种遍历的命名

　　根据访问结点操作发生位置命名：

　　① NLR：前序遍历(PreorderTraversal亦称(先序遍历))

　　——访问根结点的操作发生在遍历其左右子树之前。

　　② LNR：中序遍历(InorderTraversal)

　　——访问根结点的操作发生在遍历其左右子树之中(间)。

　　③ LRN：后序遍历(PostorderTraversal)

　　——访问根结点的操作发生在遍历其左右子树之后。

　　注意：

　　由于被访问的结点必是某子树的根，所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

遍历算法

　　1．中序遍历的递归算法定义：

　　若二叉树非空，则依次执行如下操作：

　　(1)遍历左子树；

　　(2)访问根结点；

　　(3)遍历右子树。

　　2．先序遍历的递归算法定义：

　　若二叉树非空，则依次执行如下操作：

　　(1) 访问根结点；

　　(2) 遍历左子树；

　　(3) 遍历右子树。

　　3．后序遍历得递归算法定义：

　　若二叉树非空，则依次执行如下操作：

　　(1)遍历左子树；

　　(2)遍历右子树；

　　(3)访问根结点。

　　4．层次遍历

中序遍历的算法实现

　　用二叉链表做为存储结构，中序遍历算法可描述为：

　　void InOrder(BinTree T)

　　{ //算法里①~⑥是为了说明执行过程加入的标号

　　① if(T) { // 如果二叉树非空

　　② InOrder(T->lchild)；

　　③ printf("％c"，T->data)； // 访问结点

　　④ InOrder(T->rchild);

　　⑤ }

　　⑥ } // InOrder

遍历序列

　　1．遍历二叉树的执行踪迹

　　三种递归遍历算法的搜索路线相同（如下图虚线所示）。

　　具体线路为：

　　从根结点出发，逆时针沿着二叉树外缘移动，对每个结点均途径三次，最后回到根结点。

　　2．遍历序列

　　A

　　/ /

　　B C

　　/ / /

　　D E F

　　图

　　（1） 中序序列（inorder traversal）

　　中序遍历二叉树时，对结点的访问次序为中序序列

　　【例】中序遍历上图所示的二叉树时，得到的中序序列为：

　　D B A E C F

　　（2） 先序序列（preorder traversal）

　　先序遍历二叉树时，对结点的访问次序为先序序列

　　【例】先序遍历上图所示的二叉树时，得到的先序序列为：

　　A B D C E F

　　（3） 后序序列（postorder traversal）

　　后序遍历二叉树时，对结点的访问次序为后序序列

　　【例】后序遍历上图所示的二叉树时，得到的后序序列为：

　　D B E F C A

　　（4）层序遍历（level traversal）二叉树的操作定义为：若二叉树为空，则退出，否则，按照树的结构，从根开始自上而下，自左而右访问每一个结点，从而实现对每一个结点的遍历

遍历序列

　　1．遍历二叉树的执行踪迹

　　三种递归遍历算法的搜索路线相同（如下图虚线所示）。

　　具体线路为：

　　从根结点出发，逆时针沿着二叉树外缘移动，对每个结点均途径三次，最后回到根结点。

　　2．遍历序列

　　A

　　/ /

　　B C

　　/ / /

　　D E F

　　图

　　（1） 中序序列（inorder traversal）

　　中序遍历二叉树时，对结点的访问次序为中序序列

　　【例】中序遍历上图所示的二叉树时，得到的中序序列为：

　　D B A E C F

　　（2） 先序序列（preorder traversal）

　　先序遍历二叉树时，对结点的访问次序为先序序列

　　【例】先序遍历上图所示的二叉树时，得到的先序序列为：

　　A B D C E F

　　（3） 后序序列（postorder traversal）

　　后序遍历二叉树时，对结点的访问次序为后序序列

　　【例】后序遍历上图所示的二叉树时，得到的后序序列为：

　　D B E F C A

　　（4）层序遍历（level traversal）二叉树的操作定义为：若二叉树为空，则退出，否则，按照树的结构，从根开始自上而下，自左而右访问每一个结点，从而实现对每一个结点的遍历

二叉树的存储结构

　(1）顺序存储方式

　　type node=record

　　data:datatype

　　l,r:integer;

　　end;

　　var tr:array[1..n] of node;

　　(2)链表存储方式，如：

　　type btree=^node；

　　node=record

　　data:datatye;

　　lchild,rchild:btree;

　　end;

普通树转换成二叉树

　　二叉树很象一株倒悬着的树，从树根到大分枝、小分枝、直到叶子把数据联系起来，这种数据结构就叫做树结构，简称树。树中每个分叉点称为结点，起始结点称为树根，任意两个结点间的连接关系称为树枝，结点下面不再有分枝称为树叶。结点的前趋结点称为该结点的"双亲"，结点的后趋结点称为该结点的"子女"或"孩子"，同一结点的"子女"之间互称"兄弟"。

　　普通树转二叉树，一般采用左“子女”右“兄弟”的方式来转化。

　　完全二叉树

　　对满二叉树，从第一层的结点(即根)开始，由下而上，由左及右，按顺序结点编号，便得到满二叉树的一个顺序表示。据此编号，完全二叉树定义如下：一棵具有ｎ个结点，深度为K的二叉树，当且仅当所有结点对应于深度为K的满二叉树中编号由１至ｎ的那些结点时，该二叉树便是完全二叉树。图4是一棵完全二叉树。

最后

以上就是如意丝袜为你收集整理的树——二叉树遍历的全部内容，希望文章能够帮你解决树——二叉树遍历所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。