二叉树算法题汇总前言一、适用DFS方法解题二、适用BFS（借助队列）

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

更新算法题的一些小思考

提示：以下是本篇文章正文内容，下面案例可供参考

一、适用DFS方法解题

1.判断是不是平衡二叉树

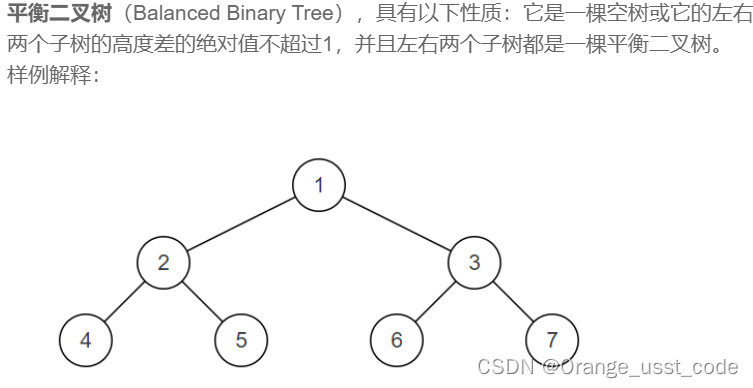
思路：自顶向下 判断根结点的左右子树是否平衡 再以左右子树为根结点判断其左右子树是否平衡

//求树的深度的函数
const dfs=(root)=>{
    if(!root)return 0
    return 1+Math.max(dfs(root.left),dfs(root.right))
}
//如果是空结点也是平衡的
if(!pRoot)return true
//求出左右子树的深度
let left=dfs(pRoot.left)
let right=dfs(pRoot.right)
//判断左右子树的深度是否满足条件
if (Math.abs(left-right)>1) return false
//要保证左右子树的子树也满足条件
return IsBalanced_Solution(pRoot.left)&&IsBalanced_Solution(pRoot.right)

2.输出二叉树中和为某一值的全部路径(1)

(只能从根结点到叶子节点)

思路：自顶向下 递归直到叶子结点 将路径保存至path[],判断是否满足目标值,有则加入res[],随着递归的回溯更新path[]

var res=[]
var path=[]
//从根节点递归到叶子结点
const dfs=(root,target)=>{
 if(!root)return
  path.push(root.val)
  //如果该结点是叶子结点 且等于目标值 加入结果集
 if(root.left===null&&root.right===null&&root.val===target){
//  深浅拷贝需注意
      res.push(path.slice())
	}
// 如果不是叶子结点 继续往下
 if(root.left||root.right){
     dfs(root.left,target-root.val)
     dfs(root.right,target-root.val)
  }
  //注意更新path数组
  path.pop()
}
	//调用函数
    dfs(root,expectNumber)
    return res

3.输出二叉树中和为某一值的全部路径(2)

（不限制从根结点到叶子 但一定是从上到小的）

function FindPath( root ,  sum ) {
    // write code here
    var res=0
    
    const dfs=(root,target)=>{
       if(!root)return
        if(root.val===target){
            res+=1
            
        }
        dfs(root.left,target-root.val)
        dfs(root.right,target-root.val) 
            

    }
    const fn=(root,target)=>{
        if(!root)return
       dfs(root,target)
        fn(root.left,target)
        fn(root.right,target)
      
    }
    fn(root,sum)
    return res
}

二、适用BFS（借助队列）

1. 从上往下打印二叉树（不分行）

思路：借助队列 当前结点的左右孩子依次加入队列 根据队列先进先出的特点 后续再弹出队头元素作为下一次循环的结点 直至队列为空

if(!root)return[]
let quene=[]
let res=[]
quene.push(root）
while(quene.length!==0){
//注意shift()是从队头删除
const node=quene.shift()
res.push(node.val)
if(node.left)quene.push(node.left)
if(node.right)quene.push(node.right)
}
return res

2. 从上往下打印二叉树（分行）

思路：基于1题的思想，每次循环向队列中添加的就是同一层的元素，因此只循环当前队列的长度即是打印一层的元素。

var res=[]
var quene=[]

if (!root)return []
quene.push(root)
while(quene.length!==0）{
	//得到当前队列的长度 既该层的元素有多少个
	const n=quene.length
	//声明一个临时数组存放当前层的元素
	var temp=[]
	for(let i=0;i<n;i++){
	const node=quene.shift()
	temp.push(node.val)
	if(node.left)quene.push(node.left)
	if(node.right)quene.push(node.right)
	}
	res.push(temp.slice())

最后

以上就是辛勤老师为你收集整理的二叉树算法题汇总前言一、适用DFS方法解题二、适用BFS（借助队列）的全部内容，希望文章能够帮你解决二叉树算法题汇总前言一、适用DFS方法解题二、适用BFS（借助队列）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。