 以下是阿鲤对二叉树的学习及理解,特此分享,希望能帮到部分同学;若有不多支出请慷慨指出。
以下是阿鲤对二叉树的学习及理解,特此分享,希望能帮到部分同学;若有不多支出请慷慨指出。
阿鲤将将以以下顺序讲解(c语言实现)
BTNode *_CreateBinTree(char *array, int size, int* index, BTDataType invalid);//二叉树的建立
BTNode *CreateBinTree(char *array, int size, BTDataType invaild);//二叉树的建立
void PreOrder(BTNode *pRoot);//前序遍历:根-》根的左子树-》根的右子树
void InOrder(BTNode *pRoot);//中序遍历:根的左子树-》根-》根的右子树
void PostOrder(BTNode *pRoot);//后序遍历:根的左子树-》根的右子树-》根
void LeveIOrder(BTNode *pRoot);//层序遍历
void DestroyBinTree(BTNode **pRoot);//二叉树的销毁
BTNode *CopyBinTree(BTNode *pRoot);//二叉树的拷贝
int GetBinTreeSize(BTNode *pRoot);//计算二叉树有多少个节点
int GetLeafCount(BTNode *pRoot);//计算二叉树中有多少个叶子节点
int GetBinTreeHeight(BTNode *pRoot);//计算树的深度
int GetKLeveNodeCount1(BTNode *pRoot,int k);//获取二叉树中第k层的节点数1
int GetKLeveNodeCount2(BTNode *pRoot, int k);//获取二叉树中第k层的节点数2
BTNode *BinaryTreeFind(BTNode *root, BTDataType x);//返回为x元素的位置
void Mirror(BTNode *pRoot);//二叉树镜像 层序
void MirrorNor(BTNode *pRoot);//检查镜像是否成功
void Swap(BTNode **left, BTNode **right);//二叉树镜像 首先附上结构定义文件(其中含有队列结构,队列结构创建是为层序遍历所准备的)
#ifndef _BINTREE_C_
#define _BINTREE_C_
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
typedef char BTDataType;
typedef struct BTNode//二叉树节点
{
struct BTNode *_pLeft;//孩子表示法
struct BTNode *_pRight;
BTDataType data;
}BTNode;
typedef BTNode* QDataType;
typedef struct QNode//队列节点
{
struct QNode* _pNext;
QDataType _data;
}QNode;
typedef struct Queue//定义两个指针,分别指向队头和队尾的节点
{
QNode * _front;//队头
QNode * _back;//队尾
}Queue;
void QueueInit(Queue *q);// 初始化
void QueuePush(Queue *q, QDataType x);//入队列
void QueuePop(Queue *q);//出队列
QDataType QueueFrount(Queue *q);//获取头
QDataType QueueBack(Queue *q);//获取尾
int QueueSize(Queue *q);//队列大小
int QueueEmpty(Queue *q);//判空
void QueueDestroy(Queue *q);//销毁
void QueueShow(Queue *q);//打印
BTNode *_CreateBinTree(char *array, int size, int* index, BTDataType invalid);//二叉树的建立
BTNode *CreateBinTree(char *array, int size, BTDataType invaild);//二叉树的建立
void PreOrder(BTNode *pRoot);//前序遍历:根-》根的左子树-》根的右子树
void InOrder(BTNode *pRoot);//中序遍历:根的左子树-》根-》根的右子树
void PostOrder(BTNode *pRoot);//后序遍历:根的左子树-》根的右子树-》根
void LeveIOrder(BTNode *pRoot);//层序遍历
void DestroyBinTree(BTNode **pRoot);//二叉树的销毁
BTNode *CopyBinTree(BTNode *pRoot);//二叉树的拷贝
int GetBinTreeSize(BTNode *pRoot);//计算二叉树有多少个节点
int GetLeafCount(BTNode *pRoot);//计算二叉树中有多少个叶子节点
int GetBinTreeHeight(BTNode *pRoot);//计算树的深度
int GetKLeveNodeCount1(BTNode *pRoot,int k);//获取二叉树中第k层的节点数1
int GetKLeveNodeCount2(BTNode *pRoot, int k);//获取二叉树中第k层的节点数2
BTNode *BinaryTreeFind(BTNode *root, BTDataType x);//返回为x元素的位置
void Mirror(BTNode *pRoot);//二叉树镜像 层序
void MirrorNor(BTNode *pRoot);//检查镜像是否成功
void Swap(BTNode **left, BTNode **right);//二叉树镜像
#endif // !_BINTREE_C_
测试函数文件
#include"BinTree.h"
void TestBinTree()
{
char *str = "ABD###CE##F##";
BTNode *pRoot = CreateBinTree(str, strlen(str),'#');
printf("前序遍历结果: ");
PreOrder(pRoot);
printf("n");
printf("中序遍历结果: ");
InOrder(pRoot);
printf("n");
printf("后序遍历结果: ");
PostOrder(pRoot);
printf("n");
LeveIOrder(pRoot);//层序遍历结果
printf("二叉树有%d个叶子节点n", GetLeafCount(pRoot));//获取叶子节点个数
printf("二叉树有%d个节点n", GetBinTreeSize(pRoot));//求二叉树中节点的个数
printf("二叉树的深度为%dn", GetBinTreeHeight(pRoot));//获取树的深度
printf("二叉树第3层的节点数为%dn", GetKLeveNodeCount1(pRoot, 3));
printf("二叉树第3层的节点数为%dn", GetKLeveNodeCount2(pRoot, 3));
BTNode * Find = BinaryTreeFind(pRoot,'B');//寻找为B的节点
printf("找到了值域为:%cn", Find->data);
Mirror(pRoot);//镜像1 层序遍历
LeveIOrder(pRoot);//层序遍历结果
MirrorNor(pRoot);//镜像2 前序遍历
LeveIOrder(pRoot);//层序遍历结果
BTNode*p = CopyBinTree(pRoot);//拷贝
LeveIOrder(p);//层序遍历结果
DestroyBinTree(pRoot);//销毁
}
int main()
{
TestBinTree();
system("pause");
return;
}
一:二叉树的创建(孩子表示法)
二叉树的创建需要使用下面两个函数
BTNode *_CreateBinTree(char *array, int size, int* index, BTDataType invalid);//二叉树的建立
BTNode *CreateBinTree(char *array, int size, BTDataType invaild);//二叉树的建立实现代码:
BTNode *BuyBinTeeNode(BTDataType data)//新建一个节点
{
BTNode *pNewNode = (BTNode*)malloc(sizeof(BTNode));
if (NULL == pNewNode)
{
assert(0);
return NULL;
}
pNewNode->data = data;
pNewNode->_pLeft = NULL;
pNewNode->_pRight = NULL;
return pNewNode;
}
BTNode *_CreateBinTree(char *array, int size, int* index, BTDataType invalid)//二叉树的创建
{
//根节点
BTNode *pRoot = NULL;
if (*index < size && array[*index] != invalid)
{
pRoot = BuyBinTeeNode(array[*index]);
++*index;
//根的左子树
pRoot->_pLeft = _CreateBinTree(array, size, index, invalid);
++*index;
//根的右子树
pRoot->_pRight = _CreateBinTree(array, size, index, invalid);
}
return pRoot;
}
BTNode *CreateBinTree(char *array, int size, BTDataType invaild)//二叉树的创建
{
//根节点
int index = 0;
return _CreateBinTree(array, size, &index, invaild);
}解析

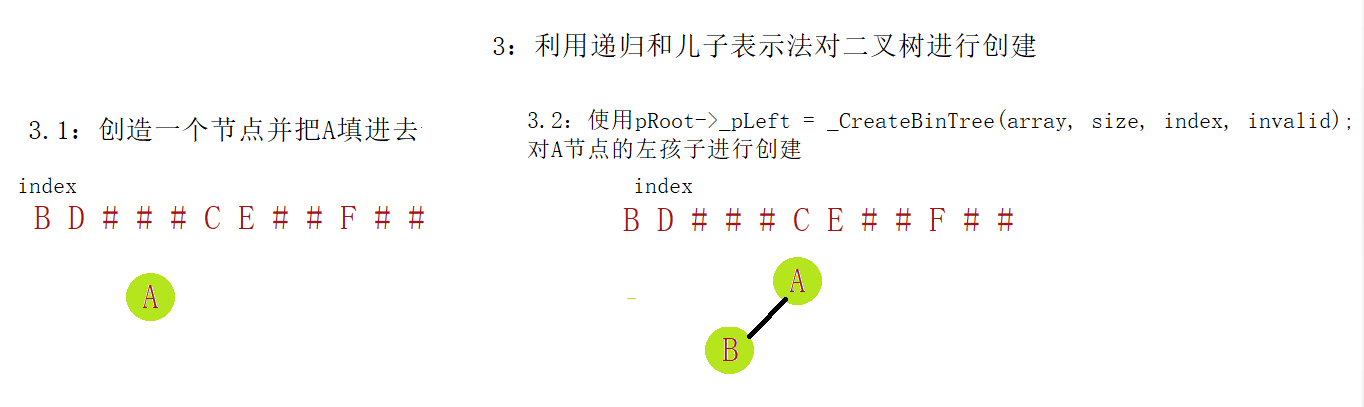

按照上面方法进行递归,便可创建好我们想要的二叉树了:
二:前序遍历,中序遍历,后序遍历
这三种遍历的方式非常类似,再此我们只介绍前序遍历
代码:
//前序遍历:根-》根的左子树-》根的右子树 递归
void PreOrder(BTNode *pRoot)
{
if (pRoot)
{
printf("%-2c", pRoot->data);
PreOrder(pRoot->_pLeft);
PreOrder(pRoot->_pRight);
}
}
//中序遍历:根的左子树-》根-》根的右子树 递归
void InOrder(BTNode *pRoot)
{
if (pRoot)
{
InOrder(pRoot->_pLeft);
printf("%-2c", pRoot->data);
InOrder(pRoot->_pRight);
}
}
//后序遍历:根的左子树-》根的右子树-》根 递归
void PostOrder(BTNode *pRoot)
{
if (pRoot)
{
PostOrder(pRoot->_pLeft);
PostOrder(pRoot->_pRight);
printf("%-2c", pRoot->data);;
}
}解析:前序遍历是按照根->根的左子树->根的右子树来进行便利的;我们的二叉树的创建就是以前序遍历的方法来实现的,所以步骤和上方是相同的:所以在此就不进行图解了。
三:层序遍历
代码:
void LeveIOrder(BTNode *pRoot)//层序遍历
{
if (NULL == pRoot)
{
return;
}
printf("层序遍历结果:");
Queue q;
QueueInit(&q);
QueuePush(&q,pRoot);
while (!QueueEmpty(&q))
{
BTNode *pCur = QueueFrount(&q);
printf("%-2c", pCur->data);
if (pCur->_pLeft)
{
QueuePush(&q, pCur->_pLeft);
}
if (pCur->_pRight)
{
QueuePush(&q, pCur->_pRight);
}
QueuePop(&q);
}
printf("n");
QueueDestroy(&q);//销毁
}
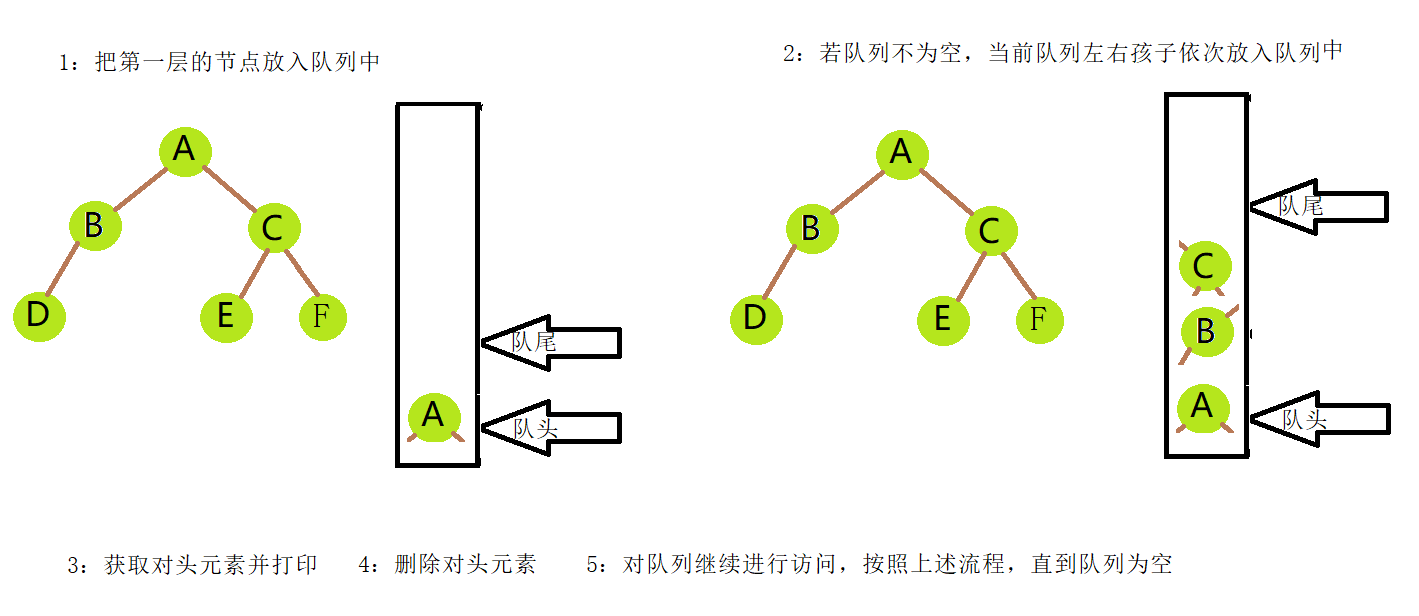
解析:层序遍历,顾名思义就是按照二叉树的层来进行遍历;对我们所创建的二叉树而言,层序遍历的结果就是
A BC DEF ;在层序遍历中我们使用了队列,对于队列的介绍请点击队列的介绍;具体分析请看下图。
四:获取叶子节点个数
代码:
int GetLeafCount(BTNode *pRoot)//计算二叉树中有多少个叶子节点
{
if (NULL == pRoot)
{
return 0;
}
if (NULL == pRoot->_pLeft)
{
return 1;
}
return GetLeafCount(pRoot->_pLeft) + GetLeafCount(pRoot->_pRight);
}
解析:计算叶子节点个数只需要对其进行递归遍历,并在其的左右节点均为NULL时候返回1,并相加
其他的都没有什么难度,阿鲤就不具体描述了,下面是全部的代码
BinTree.h
#ifndef _BINTREE_C_
#define _BINTREE_C_
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
typedef char BTDataType;
typedef struct BTNode//二叉树节点
{
struct BTNode *_pLeft;//孩子表示法
struct BTNode *_pRight;
BTDataType data;
}BTNode;
typedef BTNode* QDataType;
typedef struct QNode//队列节点
{
struct QNode* _pNext;
QDataType _data;
}QNode;
typedef struct Queue//定义两个指针,分别指向队头和队尾的节点
{
QNode * _front;//队头
QNode * _back;//队尾
}Queue;
void QueueInit(Queue *q);// 初始化
void QueuePush(Queue *q, QDataType x);//入队列
void QueuePop(Queue *q);//出队列
QDataType QueueFrount(Queue *q);//获取头
QDataType QueueBack(Queue *q);//获取尾
int QueueSize(Queue *q);//队列大小
int QueueEmpty(Queue *q);//判空
void QueueDestroy(Queue *q);//销毁
void QueueShow(Queue *q);//打印
BTNode *_CreateBinTree(char *array, int size, int* index, BTDataType invalid);//二叉树的建立
BTNode *CreateBinTree(char *array, int size, BTDataType invaild);//二叉树的建立
void PreOrder(BTNode *pRoot);//前序遍历:根-》根的左子树-》根的右子树
void InOrder(BTNode *pRoot);//中序遍历:根的左子树-》根-》根的右子树
void PostOrder(BTNode *pRoot);//后序遍历:根的左子树-》根的右子树-》根
void LeveIOrder(BTNode *pRoot);//层序遍历
void DestroyBinTree(BTNode **pRoot);//二叉树的销毁
BTNode *CopyBinTree(BTNode *pRoot);//二叉树的拷贝
int GetBinTreeSize(BTNode *pRoot);//计算二叉树有多少个节点
int GetLeafCount(BTNode *pRoot);//计算二叉树中有多少个叶子节点
int GetBinTreeHeight(BTNode *pRoot);//计算树的深度
int GetKLeveNodeCount1(BTNode *pRoot,int k);//获取二叉树中第k层的节点数1
int GetKLeveNodeCount2(BTNode *pRoot, int k);//获取二叉树中第k层的节点数2
BTNode *BinaryTreeFind(BTNode *root, BTDataType x);//返回为x元素的位置
void Mirror(BTNode *pRoot);//二叉树镜像 层序
void MirrorNor(BTNode *pRoot);//检查镜像是否成功
void Swap(BTNode **left, BTNode **right);//二叉树镜像
#endif // !_BINTREE_C_
BinTree.c
#include"BinTree.h"
BTNode *BuyBinTeeNode(BTDataType data)
{
BTNode *pNewNode = (BTNode*)malloc(sizeof(BTNode));
if (NULL == pNewNode)
{
assert(0);
return NULL;
}
pNewNode->data = data;
pNewNode->_pLeft = NULL;
pNewNode->_pRight = NULL;
return pNewNode;
}
BTNode *_CreateBinTree(char *array, int size, int* index, BTDataType invalid)//二叉树的创建
{
//根节点
BTNode *pRoot = NULL;
int count = 0;
if (*index < size && array[*index] != invalid)
{
count++;
pRoot = BuyBinTeeNode(array[*index]);
++*index;
//根的左子树
pRoot->_pLeft = _CreateBinTree(array, size, index, invalid);
++*index;
//根的右子树
pRoot->_pRight = _CreateBinTree(array, size, index, invalid);
}
return pRoot;
}
BTNode *CreateBinTree(char *array, int size, BTDataType invaild)//二叉树的创建
{
//根节点
int index = 0;
return _CreateBinTree(array, size, &index, invaild);
}
//前序遍历:根-》根的左子树-》根的右子树 递归
void PreOrder(BTNode *pRoot)
{
if (pRoot)
{
printf("%-2c", pRoot->data);
PreOrder(pRoot->_pLeft);
PreOrder(pRoot->_pRight);
}
}
//中序遍历:根的左子树-》根-》根的右子树 递归
void InOrder(BTNode *pRoot)
{
if (pRoot)
{
InOrder(pRoot->_pLeft);
printf("%-2c", pRoot->data);
InOrder(pRoot->_pRight);
}
}
//后序遍历:根的左子树-》根的右子树-》根 递归
void PostOrder(BTNode *pRoot)
{
if (pRoot)
{
PostOrder(pRoot->_pLeft);
PostOrder(pRoot->_pRight);
printf("%-2c", pRoot->data);;
}
}
void DestroyBinTree(BTNode **pRoot)//销毁使用后序
{
assert(pRoot);
if (*pRoot)
{
DestroyBinTree(&(*pRoot)->_pLeft);
DestroyBinTree(&(*pRoot)->_pRight);
free(*pRoot);
*pRoot = NULL;
}
}
int GetLeafCount(BTNode *pRoot)//计算二叉树中有多少个叶子节点
{
if (NULL == pRoot)
{
return 0;
}
if (NULL == pRoot->_pLeft)
{
return 1;
}
return GetLeafCount(pRoot->_pLeft) + GetLeafCount(pRoot->_pRight);
}
int _GetBinTreeSize(BTNode *pRoot, int *k)//计算二叉树有多少个节点
{
if (pRoot)
{
*k = *k+1;
_GetBinTreeSize(pRoot->_pLeft, k);
_GetBinTreeSize(pRoot->_pRight, k);
}
return *k;
}
int GetBinTreeSize(BTNode *pRoot )//计算二叉树有多少个节点
{
if (NULL == pRoot)
{
return 0;
}
int k = 0;
return _GetBinTreeSize(pRoot, &k);
}
int count = 0;
int _GetBinTreeHeight(BTNode *pRoot ,int *k)//计算树的深度
{
if (pRoot)
{
*k = *k + 1;
_GetBinTreeHeight(pRoot->_pLeft, k);
_GetBinTreeHeight(pRoot->_pRight, k);
}
if (*k > count)
{
count = *k;
}
*k = *k - 1;
return *k;
}
int GetBinTreeHeight(BTNode *pRoot)//计算树的深度
{
int k = 0;
_GetBinTreeHeight(pRoot, &k);
return count;
}
int _GetKLeveNodeCount(BTNode* pRoot, int k, int *m)//获取二叉树中第k层的节点数1
{
if (pRoot)
{
*m = *m + 1;
if (*m == k)
{
count++;
}
_GetKLeveNodeCount(pRoot->_pLeft,k, m);
_GetKLeveNodeCount(pRoot->_pRight,k, m);
}
if (pRoot)
{
*m = *m-1;
}
return *m;
}
int GetKLeveNodeCount1(BTNode *pRoot, int k)//获取二叉树中第k层的节点数1
{
if (NULL == pRoot || k < 0)
{
return 0;
}
count = 0;
int m = 0;
_GetKLeveNodeCount(pRoot, k, &m);
return count;
}
int GetKLeveNodeCount2(BTNode *pRoot, int k)//获取二叉树中第k层的节点数2
{
if (NULL == pRoot || k < 0)
{
return 0;
}
if (1 == k)
{
return 1;
}
return GetKLeveNodeCount2(pRoot->_pLeft, k - 1) + GetKLeveNodeCount2(pRoot->_pRight, k - 1);
}
BTNode *BinaryTreeFind(BTNode *pRoot, BTDataType x)//返回为x元素的位置
{
if (NULL == pRoot)
{
return NULL;
}
if (x == pRoot->data)
{
return pRoot;
}
BTNode *pNode = NULL;
if (pNode = BinaryTreeFind(pRoot->_pLeft, x))//左子树找
{
return pNode;
}
return BinaryTreeFind(pRoot->_pRight, x);//右子树找
}
void LeveIOrder(BTNode *pRoot)//层序遍历
{
if (NULL == pRoot)
{
return;
}
printf("层序遍历结果:");
Queue q;
QueueInit(&q);
QueuePush(&q,pRoot);
while (!QueueEmpty(&q))
{
BTNode *pCur = QueueFrount(&q);
printf("%-2c", pCur->data);
if (pCur->_pLeft)
{
QueuePush(&q, pCur->_pLeft);
}
if (pCur->_pRight)
{
QueuePush(&q, pCur->_pRight);
}
QueuePop(&q);
}
printf("n");
QueueDestroy(&q);//销毁
}
void Swap(BTNode **left, BTNode **right)//交换
{
BTNode *tmp = *left;
*left = *right;
*right = tmp;
}
void Mirror(BTNode *pRoot)//二叉树镜像1
{
if (NULL == pRoot)
{
return NULL;
}
Queue q;
QueueInit(&q);
QueuePush(&q, pRoot);
while(!QueueEmpty(&q))
{
BTNode *pCur = QueueFrount(&q);
Swap(&pCur->_pLeft, &pCur->_pRight);
if (pCur->_pLeft)
{
QueuePush(&q, pCur->_pLeft);
}
if (pCur->_pRight)
{
QueuePush(&q, pCur->_pRight);
}
QueuePop(&q);
}
}
void MirrorNor(BTNode *pRoot)//二叉树镜像2
{
if (pRoot)
{
Swap(&pRoot->_pLeft, &pRoot->_pRight);
MirrorNor(pRoot->_pLeft);
MirrorNor(pRoot->_pRight);
}
}
BTNode *CopyBinTree(BTNode *pRoot)//二叉树的拷贝
{
BTNode *pNewRoot = NULL;
if (pRoot)
{
pNewRoot = BuyBinTeeNode(pRoot->data);
pNewRoot->_pLeft = CopyBinTree(pRoot->_pLeft);
pNewRoot->_pRight = CopyBinTree(pRoot->_pRight);
}
return pNewRoot;
}
void QueueInit(Queue *q)// 初始化
{
assert(q);
q->_back = NULL;
q->_front = NULL;
}
QNode *BuyQueueNode(QDataType x)//创建一个新节点
{
QNode* pNewNode = (QNode*)malloc(sizeof(QNode));
if (NULL == pNewNode)
{
assert(0);
return;
}
pNewNode->_data = x;
pNewNode->_pNext = NULL;
return pNewNode;
}
void QueuePush(Queue *q, QDataType x)//入队列
{
assert(q);
QNode *pNewNode = BuyQueueNode(x);
if (QueueEmpty(q))
{
q->_back = pNewNode;
q->_front = pNewNode;
}
else
{
q->_back->_pNext = pNewNode;
q->_back = pNewNode;
}
}
void QueuePop(Queue *q)//出队列
{
assert(q);
if (q->_front == NULL)
{
return;
}
QNode *pDelete = q->_front;
if (NULL == q->_front)
{
q->_back = NULL;
q->_front = NULL;
}
else
{
q->_front = q->_front->_pNext;
}
free(pDelete);
}
QDataType QueueFrount(Queue *q)//获取头
{
assert(q);
return q->_front->_data;
}
QDataType QueueBack(Queue *q)//获取尾
{
assert(q);
return q->_back->_data;
}
int QueueSize(Queue *q)//队列大小
{
assert(q);
int count = 0;
QNode *pCur = q->_front;
while (pCur)
{
pCur = pCur->_pNext;
count++;
}
return count;
}
int QueueEmpty(Queue *q)//判空
{
assert(q);
return NULL == q->_front;
}
void QueueDestroy(Queue *q)//销毁
{
assert(q);
QNode *pCur = q->_front;
while (pCur)
{
q->_front = pCur->_pNext;
free(pCur);
pCur = q->_front;
}
q->_back = NULL;
q->_front = NULL;
}
void QueueShow(Queue *q)//打印
{
assert(q);
QNode *qCur = q->_front;
printf("元素是");
while (qCur)
{
printf("%-3d", qCur->_data);
qCur = qCur->_pNext;
}
printf("n");
}
test.c
#include"BinTree.h"
void TestBinTree()
{
char *str = "ABD###CE##F##";
BTNode *pRoot = CreateBinTree(str, strlen(str),'#');
printf("前序遍历结果: ");
PreOrder(pRoot);
printf("n");
printf("中序遍历结果: ");
InOrder(pRoot);
printf("n");
printf("后序遍历结果: ");
PostOrder(pRoot);
printf("n");
LeveIOrder(pRoot);//层序遍历结果
printf("二叉树有%d个叶子节点n", GetLeafCount(pRoot));//获取叶子节点个数
printf("二叉树有%d个节点n", GetBinTreeSize(pRoot));//求二叉树中节点的个数
printf("二叉树的深度为%dn", GetBinTreeHeight(pRoot));//获取树的深度
printf("二叉树第3层的节点数为%dn", GetKLeveNodeCount1(pRoot, 3));
printf("二叉树第3层的节点数为%dn", GetKLeveNodeCount2(pRoot, 3));
BTNode * Find = BinaryTreeFind(pRoot,'B');//寻找为B的节点
printf("找到了值域为:%cn", Find->data);
Mirror(pRoot);//镜像1 层序遍历
LeveIOrder(pRoot);//层序遍历结果
MirrorNor(pRoot);//镜像2 前序遍历
LeveIOrder(pRoot);//层序遍历结果
BTNode*p = CopyBinTree(pRoot);//拷贝
LeveIOrder(p);//层序遍历结果
DestroyBinTree(pRoot);//销毁
}
int main()
{
TestBinTree();
system("pause");
return;
}
输出结果:
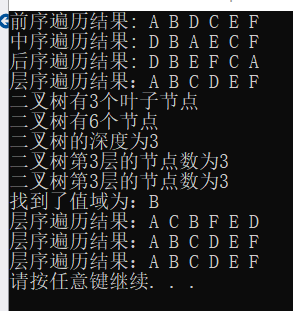
最后
以上就是标致老鼠最近收集整理的关于图解二叉树的创建及部分操作的全部内容,更多相关图解二叉树内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复