二叉树的建立以及相关操作 超详细注释の C++代码 + 代码逻辑 + 图解二叉树递归过程！

题目源自课后作业
感觉总结得还算不戳 分享出来
之前刚学二叉树的时候懵逼得一批
现在第二次接触顿时感到清晰很多
虽然只是些简单的操作 但是还是很让人有收获呐！
相信我 仔细看完 就懂啦~

1.题目要求

输入——
一个长度小于50个字符的字符串。
输出——
共有4行：

• 第1行输出中序遍历序列；
• 第2行输出后序遍历序列；
• 第3行输出叶子节点个数；
• 第4行输出二叉树深度。
  示例输入
  abc,,de,g,,f,,,
  示例输出
  cbegdfa cgefdba 3 5

2.解题思路

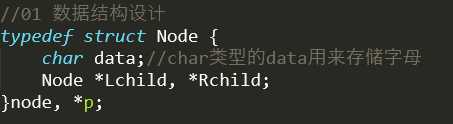
【1】定义二叉树节点数据的结构

建立一个Node结构体

{`char`一个`data`;——存数据  

 `Node`一个`*Lchild`指针 一个`*Rchild`指针;——分别指向左右子树

}最后建立一个指向Node这种结构的 `*p`指针

【2】先序建立二叉树

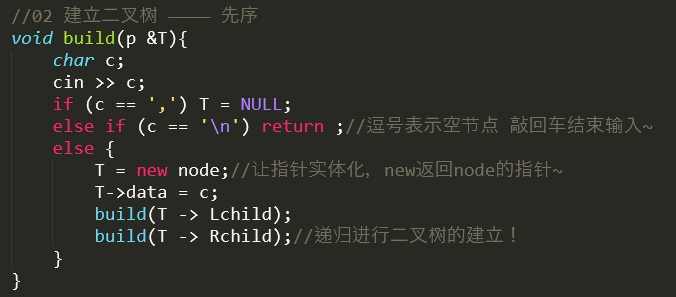
建立一个build(p & T)函数用于先序建立二叉树~

使用递归创建节点的左子树和右子树

【3】按中序、后序遍历二叉树 然后 输出序列

中序遍历——访问左子树-访问根节点-访问右子树

后序遍历——访问左子树-访问右子树-访问根节点

访问根节点时 打印该节点的data就可以完成“输出中序遍历、后序遍历序列”的要求了~

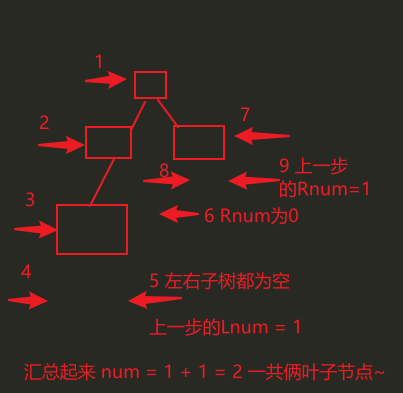
【4】求出二叉树的叶子节点个数

公式为 n0 = n2 + 1 即为 叶子节点个数为 度数为2的节点数量 + 1

首先要对 “叶子节点特性”特别熟悉——

叶子节点的左右子树为空~

其次要注意特殊情况——

二叉树为空 —— 叶子节点 = 0

二叉树只有一个节点 —— 叶子节点 = 1

排除特殊情况 二叉树叶子节点数 = 左右子树叶子节点 数量之和 —— 进行递归

肉脑想递归——记录一波

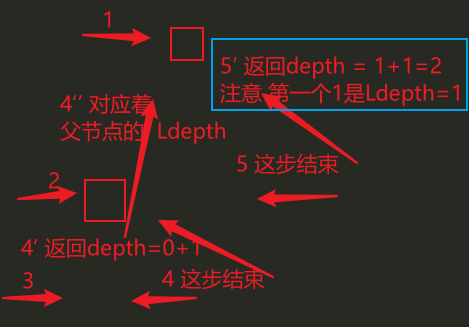
【5】求出二叉树的深度

注意特殊情况 ——

二叉树为空 —— 深度为0

二叉树只有一个节点 —— 深度为1

左右子树深度最大值 + 1

继续肉脑递归 举个简单点的例子~

跟上一个求叶子节点的方法是同理的~

左子树递归都是——

父节点的Lnum/Ldepth 都是左子节点的最终输出num/depth

右子树递归同理！

最后进行

【6】测试

3.C++代码

#include<bits/stdc++.h>
using namespace std;

//01 数据结构设计
typedef struct Node {
	char data;//char类型的data用来存储字母
	Node *Lchild, *Rchild;
}node, *p;

//02 建立二叉树 ———— 先序
void build(p &T){
	char c;
	cin >> c;
	if (c == ',') T = NULL;
	else if (c == 'n') return ;//逗号表示空节点 敲回车结束输入~
	else {
		T = new node;//让指针实体化，new返回node的指针~
		T->data = c;
		build(T -> Lchild);
		build(T -> Rchild);//递归进行二叉树的建立！
	}
}

// 03 进行中序遍历 后序遍历 并且输出结果
//中序遍历
void inorder(p T){
	if(T){
		inorder(T->Lchild);
		cout << T->data;//结束了第一个递归（T为空）后 打印出当前节点（说明已经遍历到最深的左子节点了~）
		inorder(T->Rchild);//继续进行右子树的遍历
		//我是使用多线程的思想来进行简单的肉脑递归的~
	}
}
// 后序遍历
void postorder(p T){
	if(T){
		postorder(T->Lchild);
		postorder(T->Rchild);
		cout << T->data;
	}
}

// 04 输出叶子结点数
int getLeafCount(p T){
	int num = 0, Lnum, Rnum;
	if(!T) return 0;
	else if(T -> Lchild == NULL && T -> Rchild == NULL) return 1;//两种特殊情况要考虑到~

	else {
		Lnum = getLeafCount(T->Lchild);
		Rnum = getLeafCount(T->Rchild);
		return Lnum + Rnum;
	}
}

// 05 输出二叉树的深度
int getDepth(p T){
	int depth = 0;
	if (!T) return 0;
	else {
		int Ldepth = getDepth(T->Lchild);
		int Rdepth = getDepth(T->Rchild);
		return depth = max(Ldepth, Rdepth) + 1;
	}
}

//06 测试
int main(){
	p T;
	build(T);//02 先序遍历构造树
	inorder(T);// 03 输出中序遍历结果
	cout << "t";//打印个空格 分隔开两种遍历方式的输出结果~
	postorder(T);// 03 输出后序遍历结果
	cout << endl;
	cout << getLeafCount(T) << "t" << getDepth(T) << endl;//04 05 输出叶子节点数 深度 
}

来测试下~
输入树 abc,,de,g,,f,,,

莫要忘了——先序遍历的概念嗷~

先访问根节点 然后一路遍历到最深的左子节点

递归结束条件——左子节点（为空）再访问其右子节点（也为空）

先序遍历过程如下：

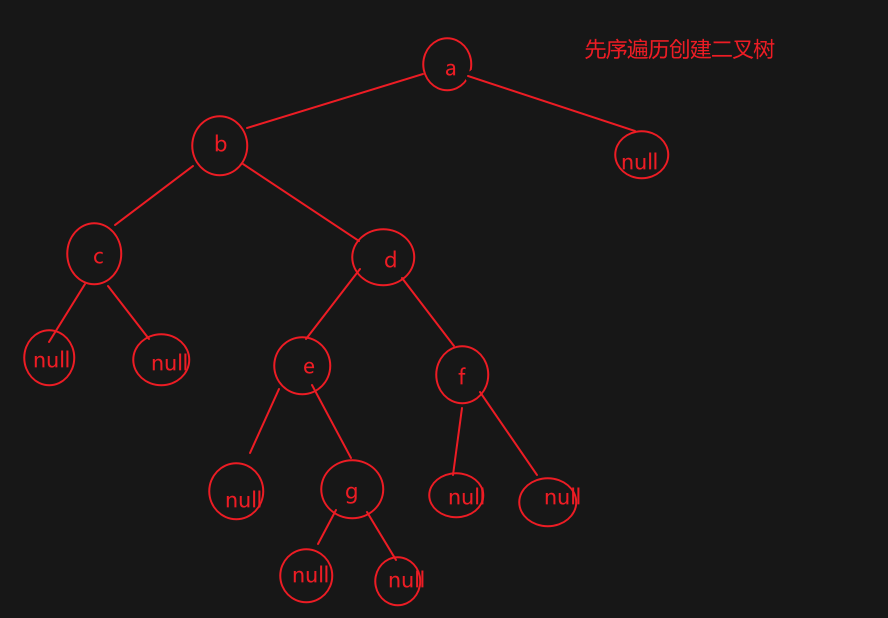
最终结果如下：

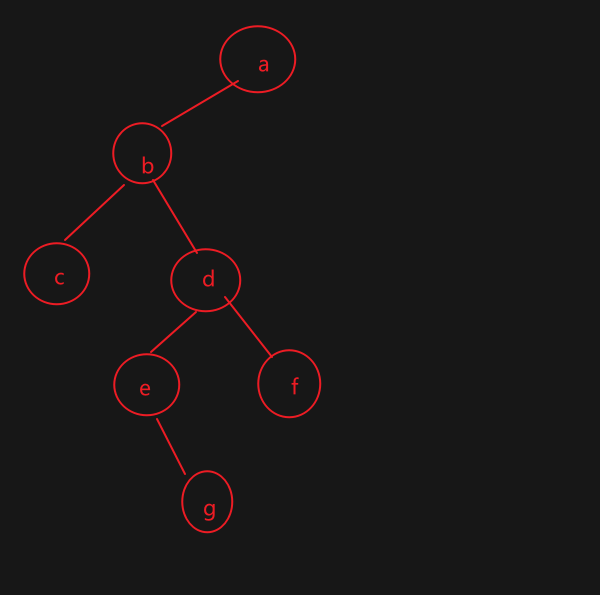
得到结果——中序遍历结果；后序遍历结果；叶子节点数；深度

最后

以上就是笨笨店员为你收集整理的二叉树的建立以及相关操作 超详细注释の C++代码 + 代码逻辑 + 图解二叉树递归过程！的全部内容，希望文章能够帮你解决二叉树的建立以及相关操作 超详细注释の C++代码 + 代码逻辑 + 图解二叉树递归过程！所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。