数据结构与算法--二叉树实现原理

二叉树

• 二叉树（binary tree）是一棵树，其中每个节点都不能有多于两个的子节点
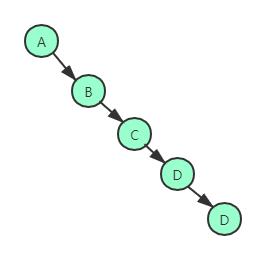
• 二叉树的一个性质是一颗平均二叉树的深度要比节点个数N小得多（重点），对二叉树的分析得出其平均深度为O($\sqrt{N}$)，而对于特殊类型的二叉树，即二叉查找树（binary search tree）其深度的平均值是O(logN)。不过极端情况如下案例，深度可以达到N-1；

实现

• 因为一个二叉树节点最多有两个子节点，所有可以保存直接连接到他们的链。树节点的声明在结构上类似双向链表，在声明中，节点就是element的信息加上两个其他节点的引用（left和right）组成的结构。

/**
 * 二叉树节点对象定义
 *
 * @author liaojiamin
 * @Date:Created in 15:24 2020/12/11
 */
public class BinaryNode {
    private Object element;
    private BinaryNode left;
    private BinaryNode right;

    public BinaryNode(Object element, BinaryNode left, BinaryNode right) {
        this.element = element;
        this.left = left;
        this.right = right;
    }

    public Object getElement() {
        return element;
    }

    public void setElement(Object element) {
        this.element = element;
    }

    public BinaryNode getLeft() {
        return left;
    }

    public void setLeft(BinaryNode left) {
        this.left = left;
    }

    public BinaryNode getRight() {
        return right;
    }

    public void setRight(BinaryNode right) {
        this.right = right;
    }
}

• 我们习惯在画链表的时候，使用矩形标识，当我们表达树的时候用圆圈，并用直线连接，因为他实际上是图（graph）。当涉及树的时候，我们也不明显的画出null节点，因为具有N个节点的每一个二叉树都需要N+1个null节点。
• 二叉树有许多与搜索无关的引用，主要的是编译器的设计领域。

案例：表达式树

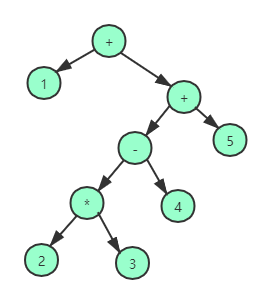
• 图中线上一个表达式树（expression tree）的案例，表达式树的叶子是操作数，如常数或者变量名，而其他的节点是操作符。由于所有操作符都是二元的（+，-，，/），因此这棵树正好可以被二叉树标识，虽然这是最简单情况，当还是可以有可能含有多于两个的子节点。一个节点也有可能只有一个儿子，如具有一目减运算符的情形。我们将通过递归计算左子树和右子树所得到的的值应用在根处的运算符而计算出表达式书T的值。在本案例中，左子树的值是无需计算，只有一个节点1， 右子树的值（23-4）+5，因此整个表达式是1+2*3-4+5
• 我们通过递归经过左节点，中节点，右节点的顺序打印表达式，这种遍历方式叫中序遍历
• 另外一种遍历策略，递归打印左节点，右节点，中节点，输出为：123*4-5++，这种输出策略称为后顺遍历
• 第三种遍历策略是先打印运算符**（中节点），然后递归打印左子树右子树**，得到的结果：+1±*2345 ，这种遍历方式叫前序遍历
• 

构造表达式树

• 我们先给出一种算法将后缀表达式转表达式树。我们已经有了将中缀表达式转后缀表达式的算法（见上一篇），因此我们能够从这两常见类型的输入生成表达式树。这里所描述的方法和后缀求职算法相似（上一篇），流程如下：
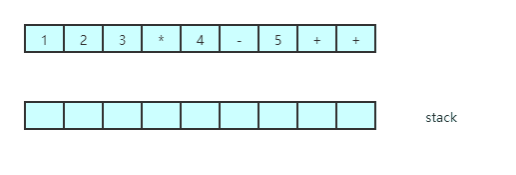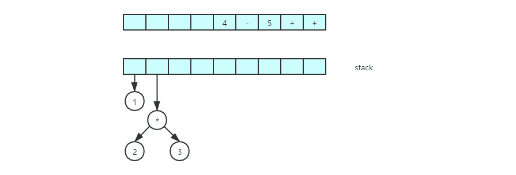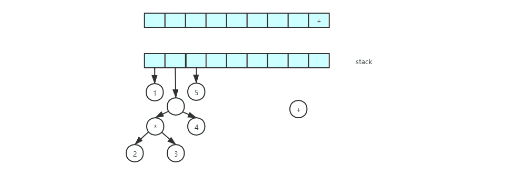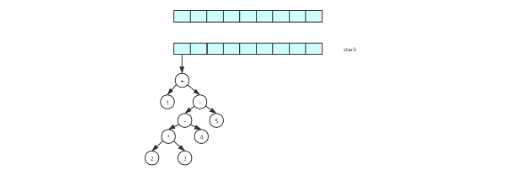
  • 我们遍历表达式，如果是符合操作数（数字），就建立一个单节点树并推入栈
  • 如果没有符合是操作符（运算符），那么将栈中弹出两个树T1，T2，（T1先出栈）
  • 将运算符，T1，T2 组成一个新的数，改树根节点是操作符，右节点是T1， 左节点是T2,
  • 将新数重新压入栈
• 还是按上面的案例（1 2 3 * 4 - 5 + +）
• 动图展示整个数构造过程
  

代码实现

/**
 * 后缀表达式 转表达式树
 *
 * @author liaojiamin
 * @Date:Created in 15:25 2020/12/11
 */
public class PostfixExTOTreeEx {
    public static BinaryNode toTreeEx(String postfixEx) {
        MyStack<Object> number = new MyStack<>();
        String[] chars = postfixEx.split(" ");
        for (String s : chars) {
            if (s.matches("([1-9]\d*\.?\d*)|(0\.\d*[1-9])")) {
                //数字
                number.push(s);
            }else if (s.matches("(\*)|(\/)|(\+)|(\-)")) {
                if (number.size() < 2) {
                    return null;
                }

                BinaryNode binaryRight = null;
                Object right = number.pop();
                if(right instanceof BinaryNode){
                    binaryRight = (BinaryNode) right;
                }else {
                    binaryRight = new BinaryNode(right, null, null);
                }

                BinaryNode binaryLeft = null;
                Object left = number.pop();
                if(left instanceof BinaryNode){
                    binaryLeft = (BinaryNode) left;
                }else {
                    binaryLeft = new BinaryNode(left, null, null);
                }
                number.push(new BinaryNode(s, binaryLeft, binaryRight));
            }
        }
        return (BinaryNode) number.pop();
    }

    /**
     * 中序遍历
     * @author: liaojiamin
     * @date: 18:15 2020/12/11
     */
    public static void printMiddleFirstTree(BinaryNode binaryNode){
        if(binaryNode == null || binaryNode.getElement() == null){
            return;
        }
        printMiddleFirstTree(binaryNode.getLeft());
        System.out.print(binaryNode.getElement());
        printMiddleFirstTree(binaryNode.getRight());
    }

    /**
     * 前序遍历
     * @author: liaojiamin
     * @date: 18:15 2020/12/11
     */
    public static void printLeftFirstTree(BinaryNode binaryNode){
        if(binaryNode == null || binaryNode.getElement() == null){
            return;
        }
        System.out.print(binaryNode.getElement());
        printLeftFirstTree(binaryNode.getLeft());
        printLeftFirstTree(binaryNode.getRight());
    }

    /**
     * 后序遍历
     * @author: liaojiamin
     * @date: 18:15 2020/12/11
     */
    public static void printRightFirstTree(BinaryNode binaryNode){
        if(binaryNode == null || binaryNode.getElement() == null){
            return;
        }
        printRightFirstTree(binaryNode.getLeft());
        printRightFirstTree(binaryNode.getRight());
        System.out.print(binaryNode.getElement());
    }

    public static void main(String[] args) {
        BinaryNode binaryNode = toTreeEx("1 2 3 * 4 - 5 + +");
        printMiddleFirstTree(binaryNode);
        System.out.println();
        printLeftFirstTree(binaryNode);
        System.out.println();
        printRightFirstTree(binaryNode);
    }

}

上一篇：数据结构与算法–链表实现以及应用
下一篇：数据结构与算法–重建二叉树

最后

以上就是超帅大白为你收集整理的数据结构与算法--二叉树实现原理的全部内容，希望文章能够帮你解决数据结构与算法--二叉树实现原理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。