二叉树的实现操作包括
//二叉树数据结构定义
/*初始化*/
//初始化二叉树的头结点
void Initiate(BiTreeNode** root);
/*左插入结点*/
//原curr结点非空,则在curr结点的左子树插入元素值为x的新结点
//原curr结点所指结点的左子树变成新插入结点的左子树
//若插入成功,返回新插入结点的指针,否则返回空
BiTreeNode* InsertLeftNode(BiTreeNode* curr, DataType x);
/*右插入结点*/
//curr结点非空,则在curr结点的右子树插入元素值为x的新结点
//原curr结点所指结点的右子树变成新插入结点的右子树
//若插入成功,返回新插入结点的指针,否则返回空
BiTreeNode* InsertRightNode(BiTreeNode* curr, DataType x);
/*左删除子树*/
//若当前结点cuee非空,则删除curr所指结点的左子树
//若删除成功返回删除节点的双亲节点指针,否则返回空
BiTreeNode* DeleteLeftNode(BiTreeNode* curr);
1.定义结构体
typedef char DataType;
//定义二叉树结点结构体
typedef struct Node
{
DataType data;
struct Node* leftchild;
struct Node* rightchild;
}BiTreeNode;2.初始化
/*初始化*/
//初始化二叉树的头结点
void Initiate(BiTreeNode** root)
{
*root = (BiTreeNode*)malloc(sizeof(BiTreeNode));
(*root)->leftchild = NULL;
(*root)->rightchild = NULL;
}3.左插入结点
/*左插入结点*/
//原curr结点非空,则在curr结点的左子树插入元素值为x的新结点
//原curr结点所指结点的左子树变成新插入结点的左子树
//若插入成功,返回新插入结点的指针,否则返回空
BiTreeNode* InsertLeftNode(BiTreeNode* curr, DataType x)
{
BiTreeNode* s, * t;
if (curr == NULL)
return NULL;
t = curr->leftchild;
s = (BiTreeNode*)malloc(sizeof(BiTreeNode));
s->data = x;
s->leftchild = t;
s->rightchild = NULL;
curr->leftchild = s;
return curr->leftchild;
}4.右插入结点
/*右插入结点*/
//curr结点非空,则在curr结点的右子树插入元素值为x的新结点
//原curr结点所指结点的右子树变成新插入结点的右子树
//若插入成功,返回新插入结点的指针,否则返回空
BiTreeNode* InsertRightNode(BiTreeNode* curr, DataType x)
{
BiTreeNode* s, * t;
if (curr == NULL)
return NULL;
t = curr->rightchild;
s = (BiTreeNode*)malloc(sizeof(BiTreeNode));
s->data = x;
s->rightchild = t;
s->leftchild = NULL;
curr->rightchild = s;
return curr->rightchild;
}5.销毁二叉树
/*销毁二叉树*/
void Destroy(BiTreeNode** root)
{
if ((*root) != NULL && (*root)->leftchild != NULL)
Destroy(&(*root)->leftchild);
if ((*root) != NULL && (*root)->rightchild != NULL)
Destroy(&(*root)->rightchild);
free(*root);
}6.左删除子树
/*左删除子树*/
//若当前结点cuee非空,则删除curr所指结点的左子树
//若删除成功返回删除节点的双亲节点指针,否则返回空
BiTreeNode* DeleteLeftNode(BiTreeNode* curr)
{
if ((curr == NULL) || (curr->leftchild = NULL))
return NULL;
Destroy(&curr->leftchild);
curr->leftchild = NULL;
return curr;
}7.右删除子树
/*右删除子树*/
//若当前结点curr非空,则删除curr所指的结点的右子树
//若删除成功返回删除结点的双亲节结点指针,否则返回空
BiTreeNode* DeleteRightNode(BiTreeNode* curr)
{
if ((curr == NULL) || (curr->rightchild == NULL))
return NULL;
Destroy(&curr->rightchild);
curr->rightchild = NULL;
return curr;
}8.前序遍历 (根左右)
/*前序遍历*/
void PreOrder(BiTreeNode* root)
{
if (root != NULL)
{
printf("%c ", root->data);
PreOrder(root->leftchild);
PreOrder(root->rightchild);
}
}9.中序遍历(左根右)
/*中序遍历*/
void InOrder(BiTreeNode* root)
{
if (root != NULL)
{
InOrder(root->leftchild);
printf("%c ", root->data);
InOrder(root->rightchild);
}
}10.后序遍历(左右根)
/*后序遍历*/
void PostOrder(BiTreeNode* root)
{
if (root != NULL)
{
PostOrder(root->leftchild);
PostOrder(root->rightchild);
printf("%c ", root->data);
}
}创建如图所示二叉树并对其进行前中后序遍历
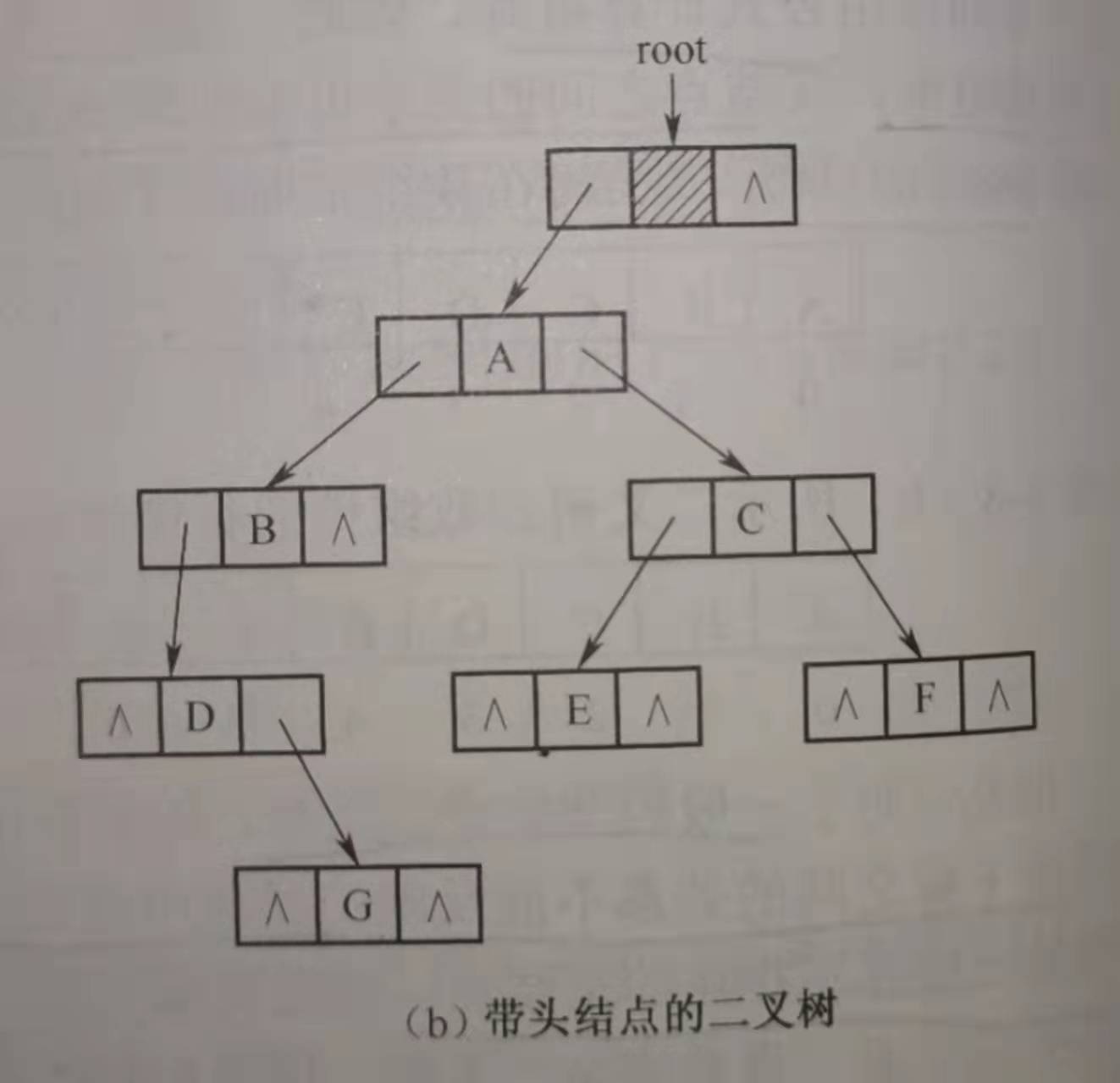
程序代码设计如下
#include<stdio.h>
#include"bitree.h" //包含二叉树头文件
int main()
{
BiTreeNode* root, * p;
Initiate(&root);
p = InsertLeftNode(root, 'A');
p = InsertLeftNode(p, 'B');
p = InsertLeftNode(p, 'D');
p = InsertRightNode(p, 'G');
p = InsertRightNode(root->leftchild, 'C');
InsertLeftNode(p, 'E');
InsertRightNode(p, 'F');
printf("前序遍历:");
PreOrder(root->leftchild);
printf("n");
printf("中序遍历:");
InOrder(root->leftchild);
printf("n");
printf("后序遍历:");
PostOrder(root->leftchild);
}程序运行结果如下
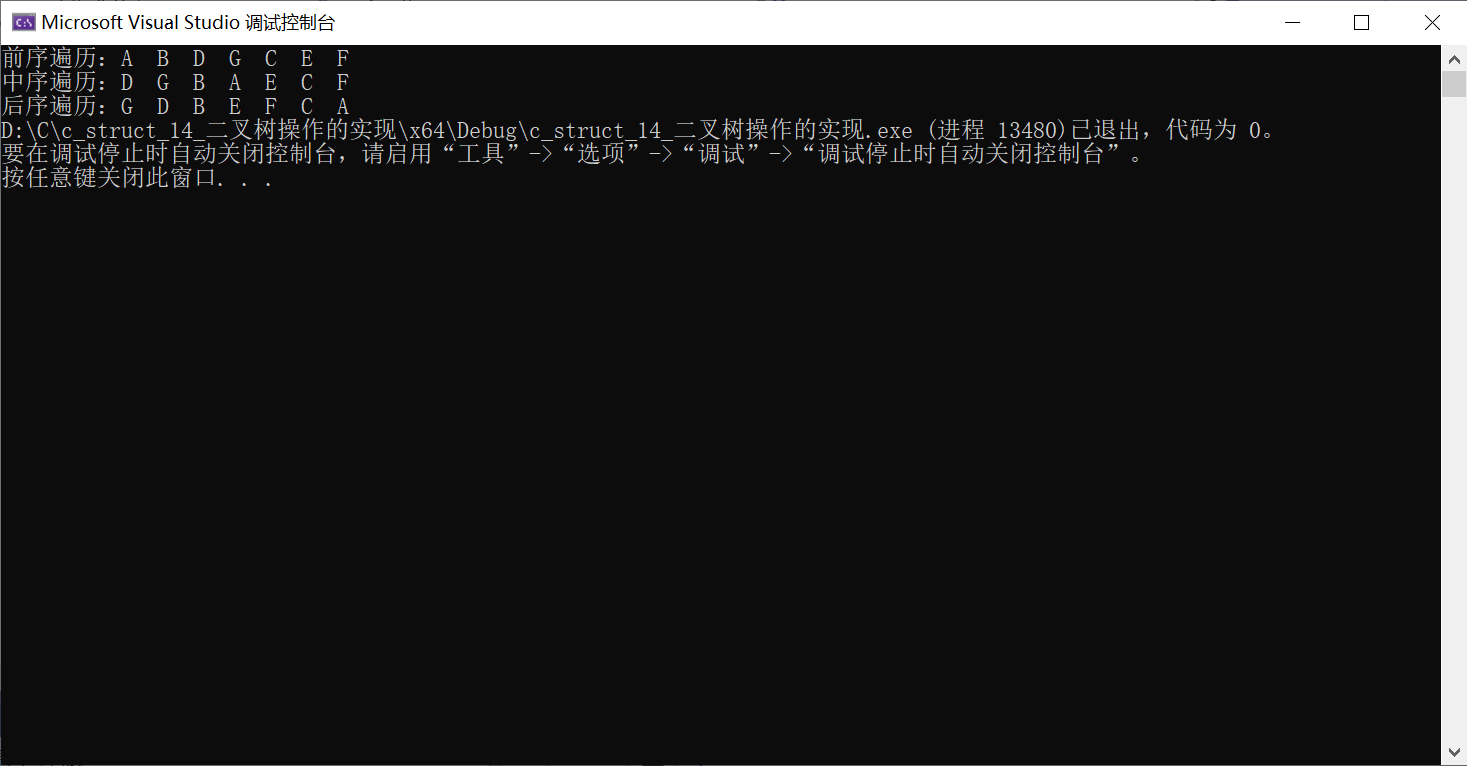
最后
以上就是顺利棒棒糖最近收集整理的关于数据结构——使用C语言 二叉树的实现及二叉树的遍历的全部内容,更多相关数据结构——使用C语言内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复