一张图！简单认识一下函数

可以先看下面这张图，了解一下函数基本概念、表示方法、特性以及分类，然后再看具体的内容。

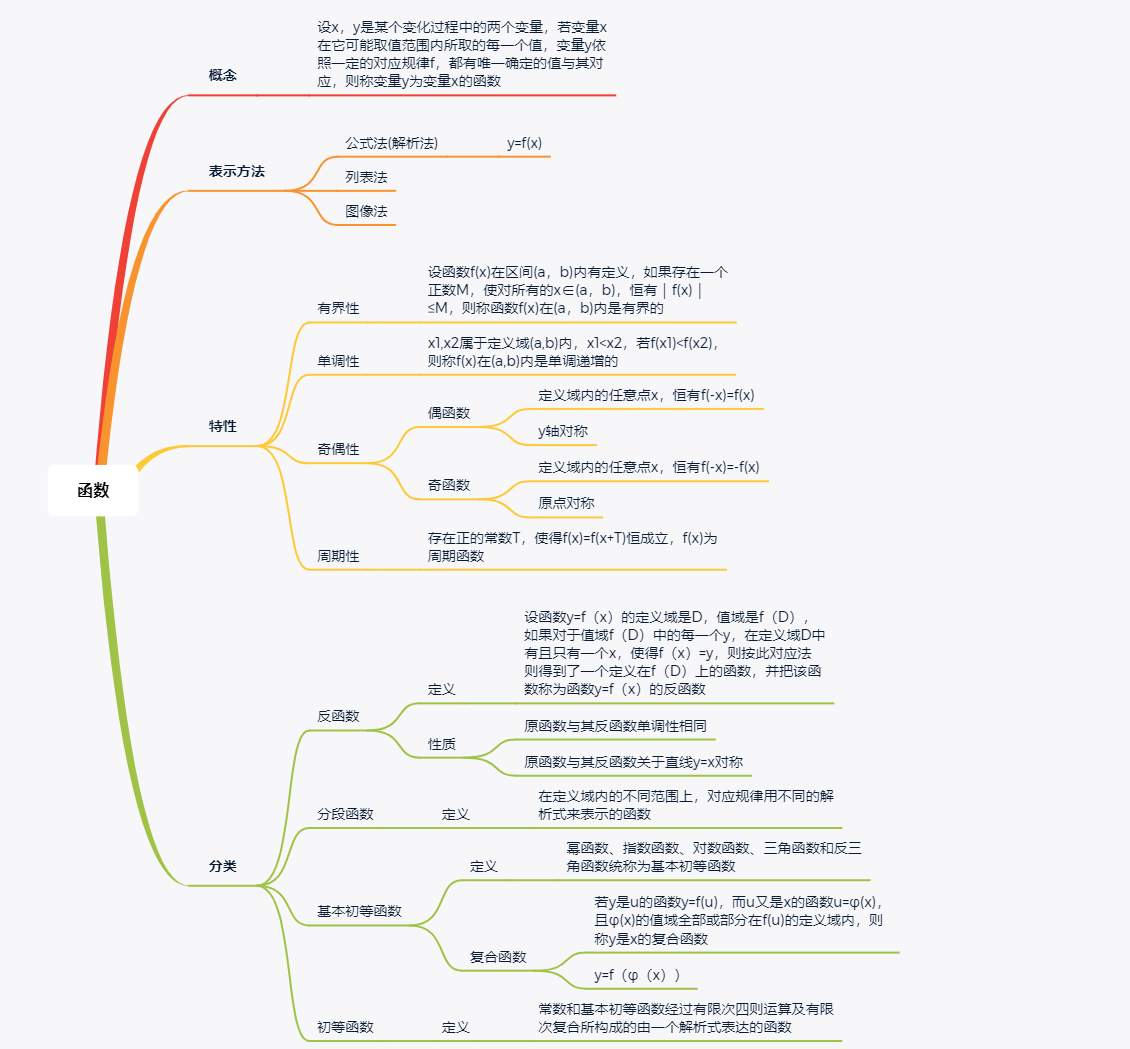
一、函数的极限

函数的极限问题，是为了估测 自变量在变化时，f(x)在定义域上的变化趋势。

1.1极限的充要条件

首先，极限存在的充分必要条件为，当x→x0时，f（x）的左右极限均存在且相等，即：

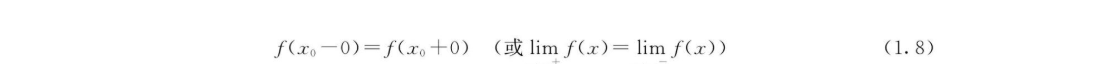
1.2 无穷小量与无穷大量

• 无穷小量是以零为极限的变量，不是数.但由于零的极限是零，所以零是可以看作无穷小量的唯一常数.
• 在自变量的某个变化过程中，limf（x）=A的充分必要条件是f（x）=A+α（x），其中α（x）为无穷小量.
• 有界函数与无穷小量的乘积仍为无穷小量
• 有限个无穷小量的和、差、积仍为无穷小

误区更正：
1）无穷大不是很大的数，而是具有非正常极限的函数，它是描述函数的一种状态.
2）切勿将[插图]认为极限存在.
3）函数为无穷大，必定无界.但反之不真

二、函数的连续性

2.1 连续的定义

• 定义1
  设函数y=f（x）在点x0的某一邻域内有定义，若当自变量x在x0点的增量Δx趋向于零时，对应的函数增量Δy=f（x0+Δx）-f（x0）也趋向于零，即
  
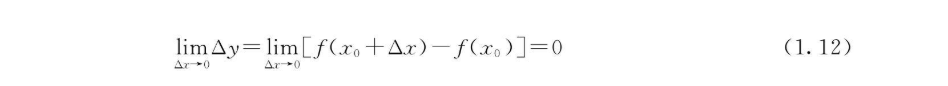
  则称函数y=f（x）在x0点连续.
• 定义2
  设函数y=f（x）在点x0的某一邻域内有定义，若f（x）当x→x0时的极限存在，且等于它在x0点的函数值f（x0），即
  
  则称函数y=f（x）在x0点连续.

2.2 连续函数

• 定义：
  如果f（x）在开区间（a，b）内每一点都连续，则称f（x）在开区间（a，b）内连续，称f（x）为（a，b）区间内的连续函数；
  如果f（x）在开区间（a，b）内连续，且在a点右连续，在b点左连续，则称f（x）在闭区间[a，b]上连续，称f（x）为[a，b]区间上的连续函数.

2.3 非连续函数(间断点)

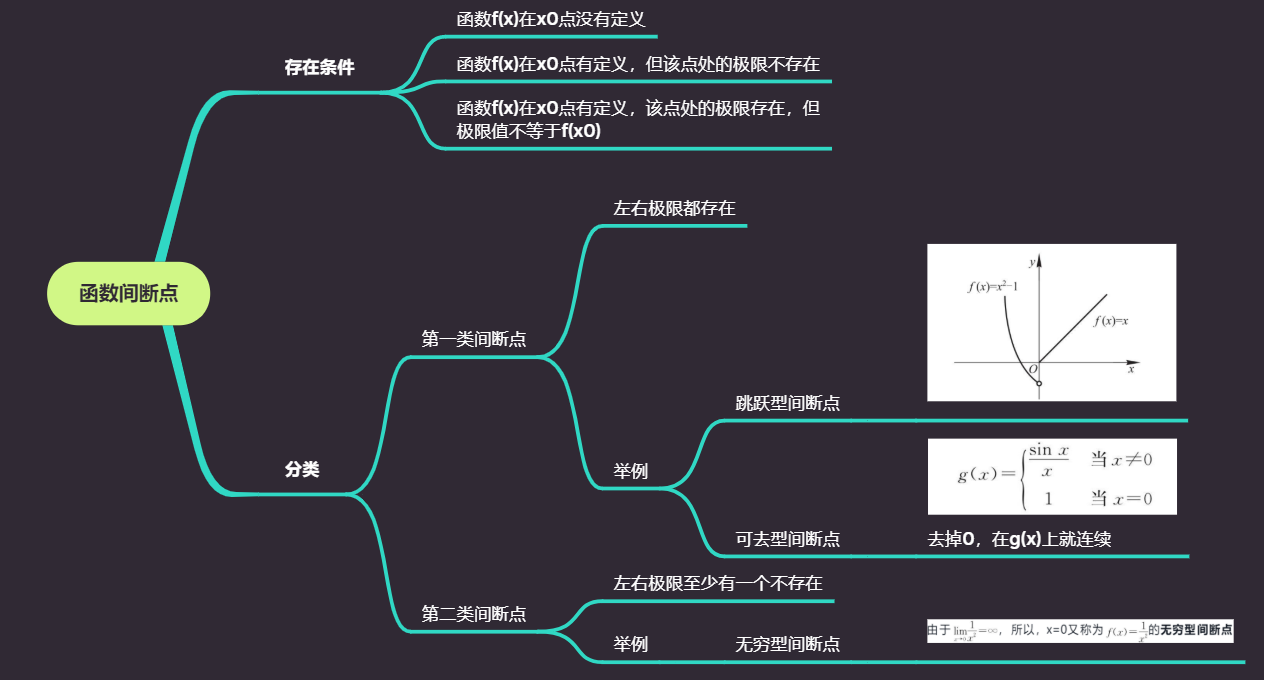
2.4 闭区间上连续函数的性质

主要有两个定理：介值定理（中间必存在值）、最大最小值定理。

• 介值定理
  
  
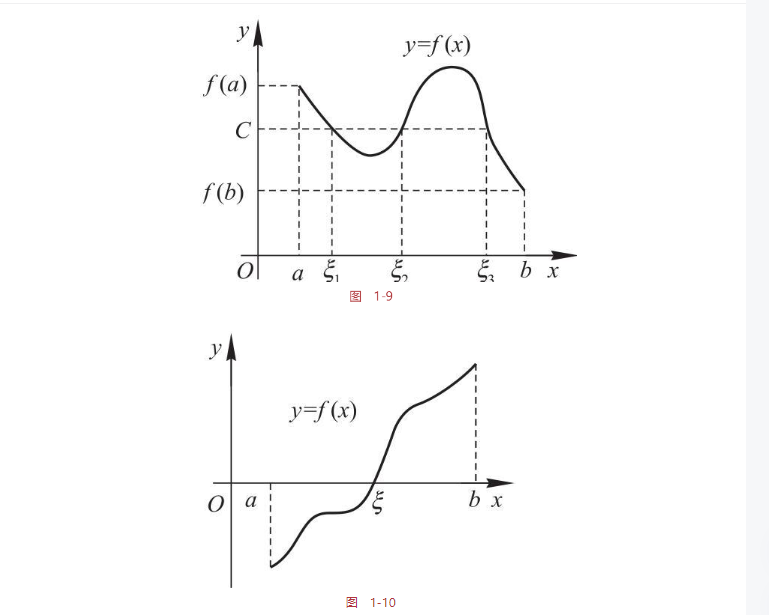
• 最大最小值定理
  设函数f（x）在闭区间[a，b]上连续，则在[a，b]上至少存在一点ξ1，使得f（ξ1）为最大值（记为M）；又至少存在一点ξ2，使得f（ξ2）为最小值（记为m）.
  

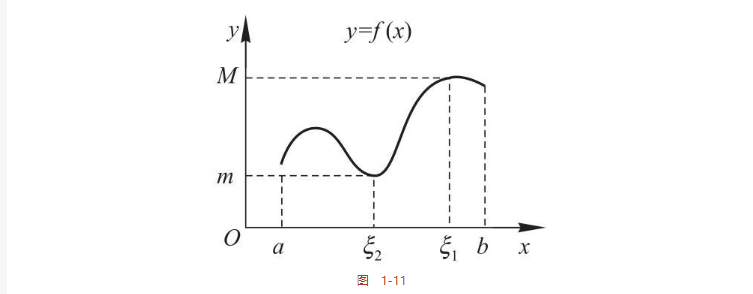
三、函数四则运算的求导法则

• 法则1　两个函数的代数和的导数（u±v）′ = u′±v′
• 法则2　两个函数乘积的导数（u·v）′=u′v+uv′
  • 推导1：（cu）′=cu′
  • 推到2：（uvw）′=u′vw+uv′w+uvw′
• 法则3　两个函数商的导数
  
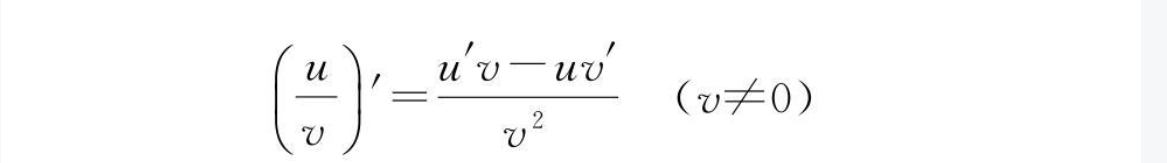
  • 推导：

四、常用函数的求导方法

4.1 复合函数的求导法则

• 法则4 （链式法则）设函数u=φ（x）在x点处可导，而函数y=f（u）在x点的对应点u（u=φ（x））处可导，则复合函数y=f（φ（x））在x点处可导，且其导数为f′（φ（x））=f′（u）φ′（x）　　或
  

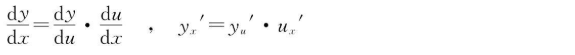
4.2 反函数的求导法则

一个函数的反函数的导数等于这个函数的导数的倒数.

• 法则5　如果函数y=f（x）在某区间Ix内单调、可导，且导数不等于零，则它的反函数x=φ（y）在对应区间Iy={y｜y=f（x），x∈Ix}上可导，且 φ’（y）= 1 / f’（x）

4.3 隐函数的求导法则

首先介绍显函数与隐函数的概念。
（1）显函数：对函数y能明确写成自变量x的解析式y=f（x）。
（2）隐函数：两个自变量x，y间的函数关系是由方程F（x，y）=0所确定的
求导技巧：
求隐函数的导数并不需要将y从方程F（x，y）=0中解出来，亦不需要引进新的法则，只要对方程F（x，y）=0的两边分别对x求导，便得到所求函数的导数.求导时注意y是x的函数，利用复合函数求导法则，便能得到所求函数的导数.
例如，求由方程ey=x2y+ex所确定的隐函数y的导数y′：

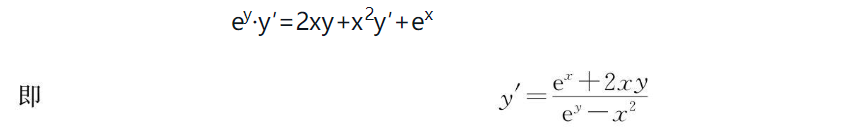
4.4 对数求导法

对数求导法：将函数的表达式两边取自然对数，并利用对数性质将表达式化简，然后应用复合函数的求导法则，将等式两边对自变量求导，最后得出函数的导数。

4.5 由参数方程所确定的函数导数

最后

以上就是秀丽小笼包为你收集整理的一张图！简单认识一下函数的全部内容，希望文章能够帮你解决一张图！简单认识一下函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。