Educational Codeforces Round 123 (Rated for Div. 2) A-E题解

69 阅读 0 评论 46 点赞

我是靠谱客的博主风中面包，最近开发中收集的这篇文章主要介绍Educational Codeforces Round 123 (Rated for Div. 2) A-E题解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

A. Doors and Keys

思路：
$模拟即可$
时间复杂度： $O n$

#include <bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define der(i,a,b) for(re i = a ; i >= b ; -- i)
#define cf int _; cin>> _; while(_--)
#define sf(x) scanf("%lld",&x)
#define pll pair<int,int> 
#define re register int
#define int long long 
#define y second 
#define x first 
using namespace std;
inline void de(auto x) {cout << x << "n" ;}
const int N = 1e6 + 10 , M = 3010 , mod = 998244353  ;

signed main()
{
    cf
    {
        string s ;
        cin >> s ;
        int a = 0 , b = 0 , c = 0 ;
        int f1 = 0 ;
        for(auto i : s)
        {
            if(i == 'r') a ++ ;
            else if(i == 'g') b ++ ;
            else if(i == 'b') c ++ ;
            else if(i == 'R')
            {
                if(a >= 1) a -- ;
                else f1 = 1 ;
            }
            else if(i == 'G')
            {
                if(b >= 1) b -- ;
                else f1 = 1 ;
            }
            else
            {
                if(c >= 1) c -- ;
                else f1 = 1 ;
            }
        }
        if(f1) puts("NO") ;
        else puts("YES") ;
    }
    return 0;
}

B. Anti-Fibonacci Permutation

思路：
$构造 a 数组为 1, 3, 2, 4, 5 . . . . . n$
$n e x t - p e r m u t a t i o n 暴力判断输出即可$
时间复杂度： $On^2$

#include <bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define der(i,a,b) for(re i = a ; i >= b ; -- i)
#define cf int _; cin>> _; while(_--)
#define sf(x) scanf("%lld",&x)
#define pll pair<int,int> 
#define re register int
#define int long long 
#define y second 
#define x first 
using namespace std;
inline void de(auto x) {cout << x << "n" ;}
const int N = 1e6 + 10 , M = 3010 , mod = 998244353  ;

int a[N] ;
 
signed main()
{
    cf
    {
        int n ;
        cin >> n ;
        fer(i,1,n) a[i] = i ;
        swap(a[2],a[3]) ;
        int k = n ;
        while(next_permutation(a + 1 , a + 1 + n))
        {
            int f1 = 0 ;
            fer(i,3,n)
            {
                if(a[i] == a[i - 1] + a[i - 2])
                {
                    f1 = 1 ;
                }
            }
            if(!f1)
            {
                k -- ;
                for(int i = 1 ; i <= n ; i ++) cout << a[i] << " " ;
                puts("") ;
            }
            
            if(!k) break ;
        }
    }
    return 0;
}

C. Increase Subarray Sums

思路：
$首先 f (i) = m a x (f (i), f (i - 1))$

$注意到 n 最大只有 5000$
$长度为 1 的子数组有 n 个$
$长度为 2 的子数组有 n - 1 个$
$. . . . . . .$
$长度为 n 的子数组有 1 个$
$所以一共有 n * (n + 1) / 2 个子数组$

$对于 f (i) 来说, 选 i 个数 + = x$
$我们可以选择所有长度 > = i 的子数组的和 + = i * x$

$设 v [i] 数组为所有长度 > = i 的子数组的和的最大值$
$求所有子数组的和可以用前缀和优化$

$那么答案即为 f (i) = m a x (v [i] + i * x, f (i - 1))$

时间复杂度： $On^2$

#include <bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define der(i,a,b) for(re i = a ; i >= b ; -- i)
#define cf int _; cin>> _; while(_--)
#define sf(x) scanf("%lld",&x)
#define pll pair<int,int> 
#define re register int
#define int long long 
#define y second 
#define x first 
using namespace std;
inline void de(auto x) {cout << x << "n" ;}
const int N = 1e6 + 10 , M = 3010 , mod = 998244353  ;

int n ;
int a[N] , s[N] , v[N] , x ;
 
signed main()
{
    cf
    {
        cin >> n >> x ;
        fer(i,1,n) sf(a[i]) , s[i] = s[i - 1] + a[i] , v[i] = -1e9 ;
        v[0] = 0 ;
        fer(len,1,n)
        {
            for(int i = 1 ; i + len - 1 <= n ; i ++)
            {
                int j = i + len - 1 ;
                v[len] = max(v[len] , s[j] - s[i - 1]) ;
            }
        }
        der(i,n-1,0) v[i] = max(v[i + 1] , v[i]) ;
        int res = 0 ;
        fer(i,0,n)
        {
            res = max(res , v[i] + i * x) ;
            cout << res << ' ' ;
        }
        puts("") ;
    }
    
    return 0;
}

D. Cross Coloring

思路：
$首先注意到题目所说$
$新颜色将应用于每个单元格，无论该单元格在操作之前是否着色$

$这意味着最后一个染色的行和列颜色永远不变, 贡献恒为 k$
$既然永远不变，我们可以删去这一行和这一列$

$所以我们可以倒着看所有染色的格子$
$如果这个格子所在的行或者列没有被染色$
$说明我们可以删去这一行或者这一列$
$贡献为 k$

$如果所有行或者所以列都被删掉, 在染色没有贡献$
$比如现在第一行和所有列都被删掉了$
$你在删第二行你会发现第二行已经被删掉了$

$答案即为上述贡献累乘即可$

时间复杂度： $O n l o g n$

#include <bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define der(i,a,b) for(re i = a ; i >= b ; -- i)
#define cf int _; cin>> _; while(_--)
#define sf(x) scanf("%lld",&x)
#define pll pair<int,int> 
#define re register int
#define int long long 
#define y second 
#define x first 
using namespace std;
inline void de(auto x) {cout << x << "n" ;}
const int N = 1e6 + 10 , M = 3010 , mod = 998244353  ;

int n , m , k , s ;
pll a[N] ;
 
signed main()
{
    cf
    {
        cin >> n >> m >> k >> s ;
        int res = 1 ;
        
        map<int,int> hh , tt ;
        fer(i,1,s) cin >> a[i].x >> a[i].y ;
        int h = 0 , t = 0 ;
        
        der(i,s,1)
        {
            if(h == n || t == m) break ;
            int f1 = 0 ;
            if(!hh[a[i].x])
            {
                f1 = 1 ;
                hh[a[i].x] = 1 ;
                h ++ ;
            }
            if(!tt[a[i].y])
            {
                f1 = 1 ;
                tt[a[i].y] = 1 ;
                t ++ ;
            }
            
            if(f1)
                res = res * k % mod;
            
        }
        
        cout << res << "n" ;
    }
    return 0;
}

E. Expand the Path

思路：
$求该机器人在 n * n 方阵中可以到达的点的数量$
$首先根据减法原理$
$可以到达的点的数量 = n * n - 无法到达的点的数量$

$现在的问题在于如何求无法到达的点的数量$

$对 s 字符串进行分类讨论$
$只包含^{'} D^{'} 或者^{'} R^{'}$
$答案必定为 n$

$同时包含^{'} D^{'} 和^{'} R^{'}$
$无非 2 种情况$
$R R . . R R D . . . . 或者是 D D . . D D R . . . . .$
首先看 $R R . . R R D . . . .$
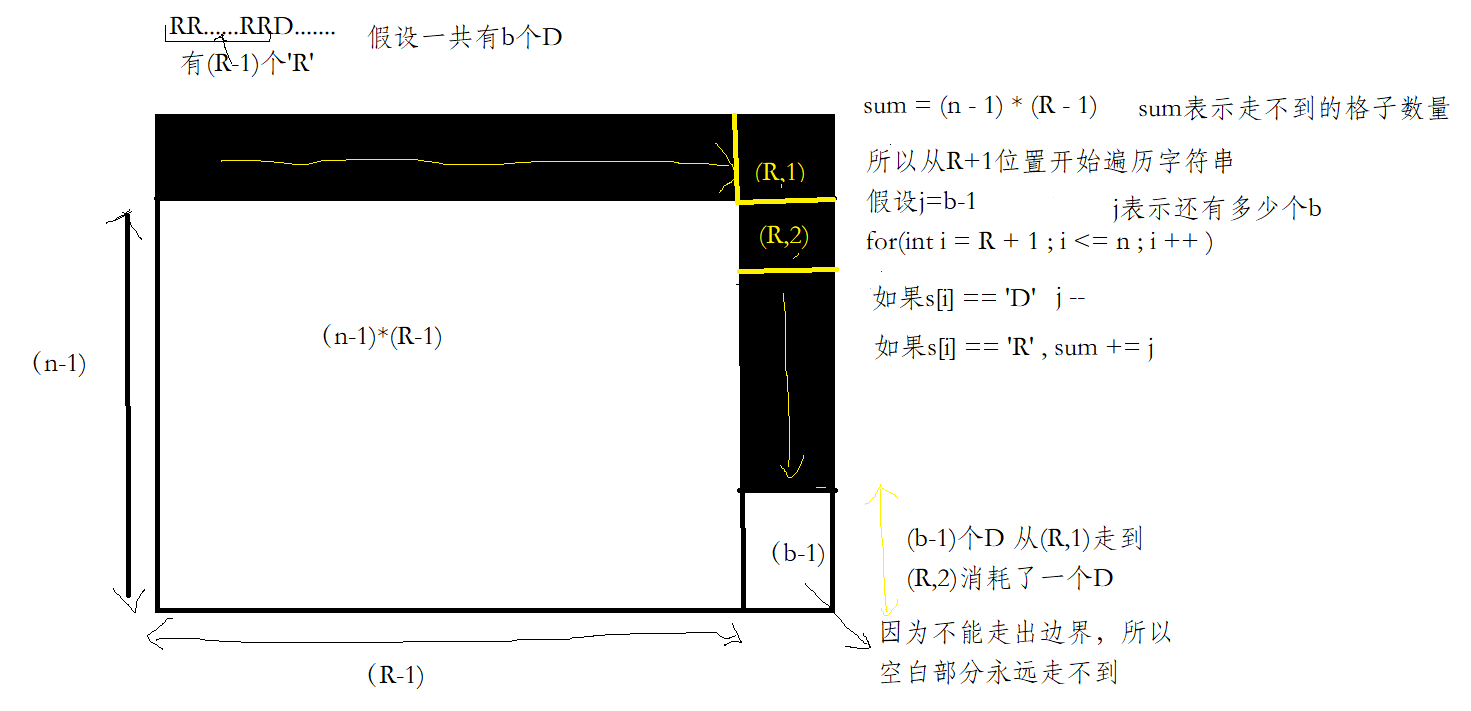
在这里插入图片描述
$图中的 j 含义有误 - 应该为从 R + 1 位置开始还有多少个^{'} D^{'} 字符$

$D D . . . . . . D D R . . . . . 同理用上述方法统计个数$
$答案即为 n * n - s u m$
时间复杂度： $O n l o g n [n 为字符串长度]$

#include <bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define der(i,a,b) for(re i = a ; i >= b ; -- i)
#define cf int _; cin>> _; while(_--)
#define sf(x) scanf("%lld",&x)
#define pll pair<int,int> 
#define re register int
#define int long long 
#define y second 
#define x first 
using namespace std;
inline void de(auto x) {cout << x << "n" ;}
const int N = 1e6 + 10 , M = 3010 , mod = 998244353  ;

int n , len ;
char s[N] ;

signed main()
{
    cf
    {
        cin >> n >> s + 1 ;
        len = strlen(s + 1) ;
        map<char,int> q ;
        fer(i,1,len) q[s[i]] ++ ;
        
        if(q.size() == 1) de(n) ;
        else
        {
            int R = 0 , D = 0 ;
            // R D 表示第一个R / D 的位置
            fer(i,1,len) 
                if(s[i] == 'R')
                {
                    R = i ;
                    break ;
                }
            fer(i,1,len)
                if(s[i] == 'D')
                {
                    D = i ;
                    break ;
                }
                
            int a = q['R'] , b = q['D'] , sum = (R - 1) * (n - 1) + (D - 1) * (n - 1) ;
            int j = a - 1 ;
            fer(i,R+1,len)
            {
                if (s[i] == 'D')
                    sum += j ;
                else {
                    j -- ;
                }
            }
            j = b - 1;
            fer(i,D+1,len)
            {
                if (s[i] == 'R')
                    sum += j ;
                else {
                    j -- ;
                }
            }
            cout << n * n - sum << "n" ;
        }
    }
    return 0;
}