【模板】一维前缀和与一维差分1.一维前缀和2.一维差分

前缀和是一种极其优秀的线性结构，也是一种重要的思想，能极大地降低区间查询的时间复杂度。

为了方便，涉及到前缀和的题目，通常使用全局数组（默认初始化为 $0$）且数组下标一般从 $1$ 开始。

1.一维前缀和

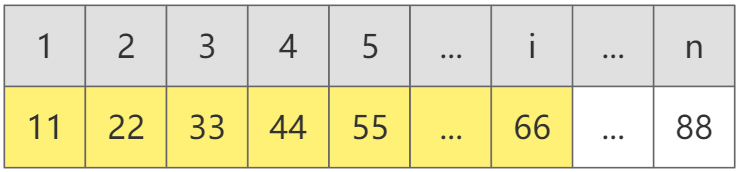
问题描述：假设有一个长度为 $n$ 的数组 a [   ] = { a 1 , a 2 , a 3 . . . . . . a n } a[ ] = left{ a_1, a_2, a_3 ...... a_n right} a[ ]={a1​,a2​,a3​......an​}，给出 $m$ 次询问，每次询问给出 $L,R$ 两个数，求数组 $a[]$ 在区间 $[L,R]$ 上的和。

如果使用暴力解法，每次都遍历一遍给出的区间，计算出答案，这样时间复杂度会达到 $O(n\ast m)$，极有可能会 TLE。

如果使用前缀和来做的话，能将时间复杂度降到 $O(n+m)$，极大地减少了时间。

1.1 求解一维前缀和数组

一维前缀和数组 $sum[i]$ 就是原数组中 $a[1]\sim a[i]$ 的总和，代码如下：

void init()
{
    for (int i = 1; i <= n; i++)
    {
        sum[i] = sum[i - 1] + a[i];
    }
}

1.2 区间查询

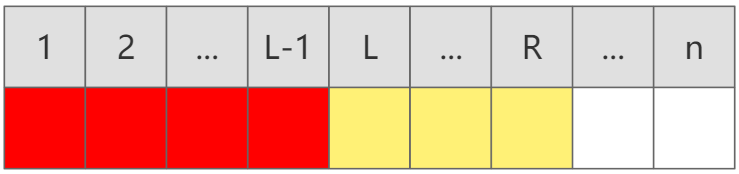
原数组 $a[]$ 在区间 $[L,R]$ 上的和为 sum[R] - sum[L - 1]，代码如下：

int get(int L, int R)
{
    return sum[R] - sum[L - 1];
}

2.一维差分

2.1 定义

假设有原数组 a [   ] = { a 1 , a 2 , a 3 , . . . , a n } a[ ] = left{a_1, a_2, a_3, ... , a_nright} a[ ]={a1​,a2​,a3​,...,an​}，现构造出一个数组 b [   ] = { b 1 , b 2 , b 3 , . . . , b n } b[ ] = left{b_1, b_2, b_3, ... , b_nright} b[ ]={b1​,b2​,b3​,...,bn​}，使得 $a_i=b_1+b_2+...+b_i$，那么 $b[]$ 就称为 $a[]$ 的差分，$a[]$ 就称为 $b[]$ 的前缀和。

可以发现，差分与前缀和是逆运算。

2.2 区间修改

由上述定义可知，差分数组 $b[i]$ 的前缀和就是原数组 $a[i]$ 的值。

利用差分数组 $b[]$ 可以快速地对原数组 $a[]$ 进行区间修改，时间复杂度为 $O(1)$。

假如现在要将原数组 $a[]$ 在区间 $[L,R]$ 上的每个数都加上 $x$，那么通过上述定义可以知道：

• 第一个受影响的差分数组中的元素为 $b[L]$，令 b[L] += x，那么 $L$ 及其后面的原数组元素在计算过程中都会加上 $x$。

• 最后一个受影响的差分数组中的元素为 $b[R]$，令 b[R + 1] −= x，那么可以保证不会影响 $R$ 后面的原数组元素的计算。

这样一来，就不必对区间内每一个数进行处理，只需处理两个端点即可。

void add(int L, int R, int x)
{
    b[L] += x;
    b[R + 1] -= x;
}

2.3 初始化

问题：一维差分数组 $b[]$ 是如何构造出来的呢？

差分数组 $b[]$ 可以直接通过原数组 $a[]$ 的相邻元素相减得到。

$$b[i]=a[i]-a[i-1]$$

事实上，我们不需要过分关注差分数组 $b[]$ 是怎么构造出来的，只需要知道差分与前缀和是互逆运算即可。

一开始，可以把原数组 $a[]$ 想象成全是 $0$，即 a [   ] = { 0 , 0 , 0 , . . . 0 } a[ ] = left{0, 0, 0, ... 0right} a[ ]={0,0,0,...0}，此时相应的差分数组 $b[]$ 也全是 $0$， 即 b [   ] = { 0 , 0 , 0 , . . . 0 } b[ ] = left{0, 0, 0, ... 0right} b[ ]={0,0,0,...0}。

接下来，对原数组 $a[]$ 的初始值可以做如下考虑：

• $a[1]$ 相当于区间 $[1,1]$ 的每个数都加上 $a[1]$，即 add(1, 1, a[1])

• $a[2]$ 相当于区间 $[2,2]$ 的每个数都加上 $a[2]$，即 add(2, 2, a[2])

• …

• $a[n]$ 相当于区间 $[n,n]$ 的每个数都加上 $a[n]$，即 add(n, n, a[n])

这样，利用区间修改操作 $add()$ 即可完成赋初始值，从而避免了手动构造差分数组 $b[]$。

最后

以上就是魁梧人生为你收集整理的【模板】一维前缀和与一维差分1.一维前缀和2.一维差分的全部内容，希望文章能够帮你解决【模板】一维前缀和与一维差分1.一维前缀和2.一维差分所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。