二维DP问题前言小技巧例题 1例题 2例题 3

前言

我们经常会碰到二维DP问题，比如给你一张地图（一般是二维矩阵），让你计算出从地图的左上端走到右下端的路径有多少条 / 最短的路径之和，这种问题一般会被限制运动的空间（至少我现在所碰到的题目），一般是只能向下和向右移动。

我对dp问题理解不深，对于二维dp问题我的理解就是找出最优子结构（递推方程）之后，用一个二维数组来保存历史状态就能解决问题了

小技巧

一般这种问题很容易被矩阵上边和左边这两条boundary把程序搞得很复杂（因为这两个boundary需要修改特定的递推公式程序），我们在开辟二维dp数组时，把长和宽都+1，然后从（i，j）=（1，1）开始遍历，这样就不会遇到boundary问题了

其次就是dp数组压缩，我们可以观察到，其实我们的二重嵌套循环就是每次循环一行，然后对于这一行的每一个元素，都根据他的dp[left]和dp[up]来对他进行更新，而我们可以使用一个映射，将这种二维关系（dp[left]和dp[up]）映射成一维关系（意思就是我们只用使用一个一维的DP数组即可）

比如

if col == 0
	dp[col] = f(dp[col])// 这是因为现在的dp[up]就是dp[col]，而col=0时，dp[col]的左边没东西
else 
	dp[col] =  f(dp[col-1], dp[col])//这是因为此时 dp[left] = dp[col-1], dp[up] = dp[col]

通过上面的伪代码，你一定明白了如何将二维dp数组压缩为一维dp数组吧

例题 1

这是非常经典的一道二维dp题目了，我们的解决方法有两种：求组合数和DP求解。

DP求解的话，这个问题的最优子结构为：
$$dp[curr]=dp[left]+dp[up]$$

62. Unique Paths
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1:

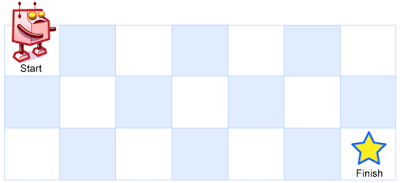
Input: m = 3, n = 7
Output: 28
Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

方法一 求组合数

因为机器人只能向右或者向下走，而机器人一共要走 width + height 步，所以总的走法就是一个组合数 : C(n, m)，其中n为height+weight， m为weight或者height

class Solution {
   
public:
    int uniquePaths(int m, int n) {
   
        if(m == 1 || n == 1)
            return 1;
        m--, n--;
        if(m < n) swap(m, n);
        long res = 1;
        for(int i = m+1, j=1; i 

最后

以上就是潇洒龙猫为你收集整理的二维DP问题前言小技巧例题 1例题 2例题 3的全部内容，希望文章能够帮你解决二维DP问题前言小技巧例题 1例题 2例题 3所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。