最大和问题（一维数组和二维数组）（dp问题）

dp问题一直是比较头疼的问题，现在介绍两个较为相似的问题；

1 .一维的最大和问题：Max Sum HDU - 1003

2.二维的最大和问题：题目1139：最大子矩阵

【一维最大和】

以样例讲：给你n个整数，问连续的几个数的和最大是多少?(即最大字串是多少）
该题有几个要求：
（1）要求和相同时，取最开始的；
（2）须输出起始位置；

         输入   0 6 -1 1 -6 7 -5
         输出   7 1 6   （最大值 起始位置 结束位置）

    思路：从第一个非负的整数开始查找，如果加上下一个整数，和变成了负 数（0不是负数），那么从这个负数开始继续查找（这是为了防止整个序列都是负数的情况），否则继续向下加，并记录一下下标。
     代码：

#include<stdio.h>
#include<string.h>
int tt;
void findmax(int a[100],int n)
{
    int sum=a[0],x=0,y=0;//及时更新查找的位置和最大值
    int max=a[0],max_x=0,max_y=0;//记录最终的最大值和位置
    for(int i=1; i<n; i++)
    {
        if(sum>=0)
        {
            sum+=a[i];
            y=i;
        }
        else
        {
            sum=a[i];
            x=y=i;
        }
        if(max<sum)
        {
            max=sum;
            max_x=x;
            max_y=y;
        }
    }
    printf("Case %d:n%d %d %dn",tt++,max,max_x+1,max_y+1);
}

int main()
{
    int t;
    int map[100009];
    scanf("%d",&t);
    tt=1;
    int flag=0;
    while(t--)
    {
        if(flag) printf("n");
        flag=1;
        scanf("%d",&n);
        for(int i=0; i<n; i++)
            scanf("%d",&map[i]);
        findmax(map,n);
    }
    return 0;
}

【二维最大和】

    给你n*m个数，从中选出一个子矩阵，使其和最大（即最大子矩阵）

      输入    4
             0 -2 -7 0
             9 2 -6 2
             -4 1 -4  1
             -1 8  0 -2

   输出      15 

思路：这个问题与“最大子序列”的问题很像，只是二维的，所以我们要将它转化为一 维的问题；
        如果将一个二维矩阵，压缩为一维矩阵，那问题不就解决了（其实我当时也绕不过来这个弯儿，慢慢想）。

          如何将一个二维矩阵压缩为一维的呢？
         首先矩阵是一个矩形，如果其最大子矩阵与原矩阵等高，是否就可以压缩为一维矩阵了。
     看图更好理解：

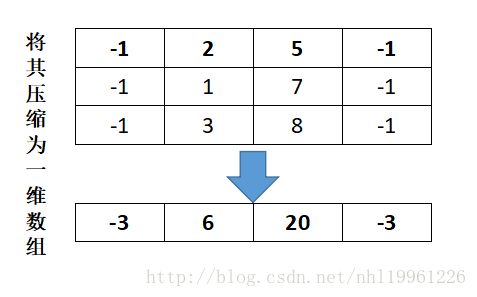
按照这种方式查找所有的子矩阵；
下方是代码：(n*m的矩阵与n*n的矩阵在代码中介绍）

#include<stdio.h>
#include<string.h>
#define inf 0x3f3f3f3f

int findmax(int a[100],int n)//将二维转化为一维数组查找最大子序列（即查找最大子矩阵）
{
    int sum=a[0];
    int max_=a[0];
    for(int i=1; i<n; i++)
    {
        if(sum>=0)
            sum+=a[i];
        else
            sum=a[i];
        if(max_<sum)
            max_=sum;
    }
     return max_;
}

int main()
{
    int a[100][100];//原矩阵
    int b[100];//记录子矩阵的一维数组（上面介绍的）
    int n;
    int max;//记录最大和
    while(~scanf("%d",&n))
    {
        max=-inf;
        for(int i=0; i<n; i++)
            for(int j=0; j<n; j++)
                scanf("%d",&a[i][j]);
        for(int k=0; k<n; k++)//以每一行作为子矩阵的上边界（0~n）
        {
            memset(b,0,sizeof(b));//子矩阵压缩为一维的数组；
            for(int i=k; i<n; i++)//以每一行作为子矩阵的下边界（k~n）
            {
                for(int j=0; j<n ; j++)//压缩子矩阵的过程（如果是n*m的矩阵,将这一行的n改为m）
                    b[j]+=a[i][j];
                int sum=findmax(b,n);//查找最大子序列（如果是n*m的矩阵,将这一行的n改为m)
                if(sum>max)  max=sum;//记录最大值
            }
        }
        printf("%dn",max);
    }
    return 0;
}

最后

以上就是平常芹菜为你收集整理的最大和问题（一维数组和二维数组）（dp问题）的全部内容，希望文章能够帮你解决最大和问题（一维数组和二维数组）（dp问题）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。