所谓0/1背包问题,就是指每个元素最多选取一次的背包问题,所有背包问题的变种,可以说都来自于0/1背包问题。
原始的0/1背包问题
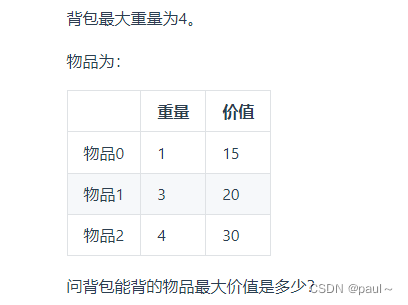
二维dp数组解法
1.dp数组的定义与初始化
dp[i][j]表示背包容量为j时 任意取下标为[0-i]物品进行放置 背包中的最大价值 当背包容量为0时 dp[i][0] 背包中的价值只能为0 只放物品0时 背包容量小于物品重量时 dp[0][j]为0 背包容量大于物品重量时 dp[i][0]为value[0]
按下图进行dp数组的初始化
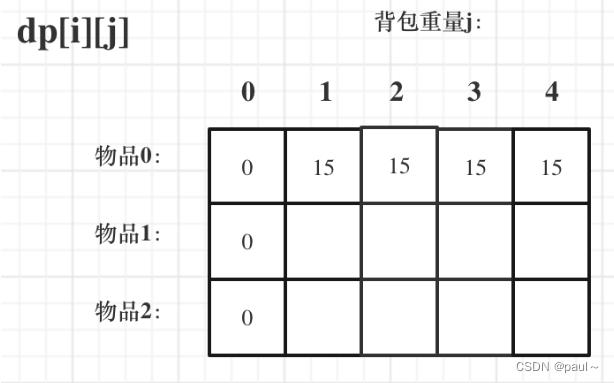
2.dp数组的推导公式
递推公式由两个方向推导而来 不放物品i 与 放物品i 不放物品i 保持i-1状态不变 dp[i][j] = dp[i - 1][j] 放物品i时 dp[i][j] = dp[i-1][j-weight[i]] 为背包容量为j -weight[i]的时候不放物品i的最大价值 再加上value[i] 取上述两种选择中的dp最大值
3.dp数组的遍历顺序
无论是先遍历物品数量 还是先遍历背包容量 都达到了一致的效果
4.Java代码如下:
public class bagdemo {
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
bag_problem_test(weight, value, bagsize);
}
public static void bag_problem_test(int[] weight, int[] value, int bagsize) {
int w_len = weight.length;//物品个数
// 定义dp数组:
// dp[i][j]表示背包容量为j时 任意取前i个物品进行放置 背包中的最大价值
// 此处初始化应该bagsize+1
int[][] dp = new int[w_len][bagsize + 1];
// 当背包容量为0时 dp[i][0] 背包中的价值只能为0
for (int i = 0; i < w_len; i++) {
dp[i][0] = 0;
}
// 只放物品0时 背包容量小于物品重量时 dp[0][j]为0
for (int j = 0; j < weight[0]; j++) {
dp[0][j] = 0;
}
for (int j = weight[0]; j <= bagsize; j++) {
dp[0][j] = value[0];
}
// 递推公式由两个方向推导而来 不放物品i 与 放物品i
for (int i = 1; i < w_len; i++) { // 遍历物品
for (int j = 0; j <= bagsize; j++) { // 遍历背包容量
// 当背包容量小于第i件物品重量时 还是i-1状态不变
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else {
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j- weight[i]] + value[i]);
}
}
}
//打印dp数组
for (int i = 0; i < w_len; i++) {
for (int j = 0; j <= bagsize; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.print("n");
}
}
}
5.输出的dp数组结果:
可放置的物品最大价值即为:dp[weight.length][bagsize] = 35
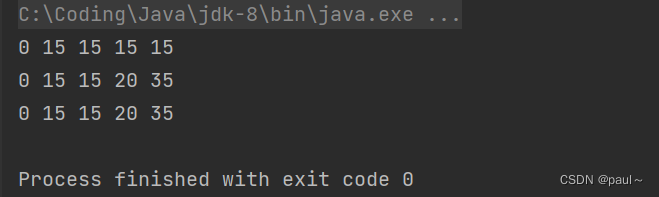
一维数组解法:
1.dp数组的定义与初始化:
上述二维dp数组 dp[i][*]都是基于上一层 dp[i-1][*]得到的 所以可以压缩成一个一维dp数组 不断滚动更新 一维dp数组的含义 容量为j的背包 所背物品的最大价值为dp[j] 将dp全部初始化为1即可
2.dp数组的推导公式:从两个方向选取的思路同上
3.dp数组的遍历顺序:此处应特别注意:
物品和背包的遍历顺序不能更改 必须先物品 再背包 且遍历背包时 必须为倒序遍历 因为要基于上一层尚未滚动更新的状态
4.Java代码如下:
public class bagdemo2 {
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
bag_problem_test(weight, value, bagsize);
}
private static void bag_problem_test(int[] weight, int[] value, int bagsize) {
// 二维dp数组 dp[i][*]都是基于上一层 dp[i-1][*]得到的
// 所以可以压缩成一个一维dp数组 不断滚动更新-
// 一维dp数组的含义 容量为j的背包 所背物品的最大价值为dp[j]
int[] dp = new int[bagsize+1];
// 初始化为0
for(int j =0 ; j <= bagsize; j++){
dp[j] = 0;
}
// 此处物品和背包的遍历顺序不能更改 必须先物品 再背包
for (int i =0 ; i < weight.length; i++){ // 遍历物品
for(int j = bagsize; j >= weight[i]; j--){ //遍历背包容量
// 必须为倒序遍历 因为要基于上一层尚未滚动更新的状态
dp[j] = Math.max(dp[j], dp[ j-weight[i] ] + value[i]);
}
}
for(int j =0; j <= bagsize; j++){
System.out.print(dp[j]+" ");
}
}
}
5.输出dp数组的结果:
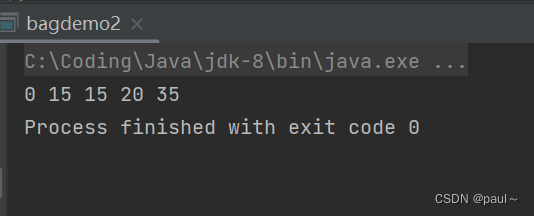
即可放置的物品最大价值即为:dp[bagsize] = 35
参考内容:代码随想录
最后
以上就是闪闪大侠最近收集整理的关于0/1背包问题(一)的全部内容,更多相关0/1背包问题(一)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复