【算法-LeetCode】64. 最小路径和（动态规划；二维数组；滚动数组）64. 最小路径和 - 力扣（LeetCode）

64. 最小路径和 - 力扣（LeetCode）

发布：2021年9月12日10:05:30

问题描述及示例

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

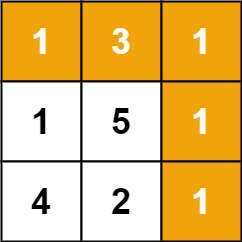
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

我的题解

因为之前做过了几道动态规划的题目，所以看到这道题目的时候还是比较容易就能看出是用动态规划来做的。有关动态规划的解题步骤可以参看我之前写的这篇博客：

参考：【算法-LeetCode】53. 最大子序和（动态规划初体验）_赖念安的博客-CSDN博客

里面也有我做过的其他动态规划类型的相关题目，都有比较详细的过程展示。

我的题解1（动态规划—二维dp数组）

更新：2021年9月14日09:52:26

因为这道题思路比较简单，解出来的时候还挺开心的，感觉也没有遇到特别难跨的坎，所以当时忘了写过程记录。现在补上吧。

其实我觉得如果碰上这种可以用二维 dp 数组的动态规划题，首先就得弄明白二维数组的解法，然后在根据滚动数组的思路来将二维数组优化为一维数组。如果一上来就用一维数组的解法，很可能就会对这道题的解题过程处于一知半解的状态。

1、单独初始化首行和首列

根据上面总结的动态规划的常用思路。这道题的解题思路如下：

①确定 dp 数组表示的含义。也就是明确 dp 数组里存的到底是什么。dp[i][j] 表示的是由 起点位置（也就是 grid[0][0]）到 grid[i][j] 的所有路径和中的那个最小值。

②初始化 dp 数组。这一步往往要和【③确定状态转移方程】中所涉及到的下标取值结合在一起思考。

• 因为我是采用二维数组来表示 dp 数组的，所以一开始肯定是要创建一个指定长宽的二维数组，而这里的话我是让 dp 数组和grid 数组保持同样的长宽。同时我还给每个 dp 数组中的元素填充了一个默认值 0（其实这里填其他值也可以，因为最后都会被状态转移方程的计算结果所覆盖）。
  
  

  初始化 dp 数组时遇到的小问题：
  其实一开始我把 dp 数组的长宽设置为分别比grid 的长宽大 1 的，如下图所示：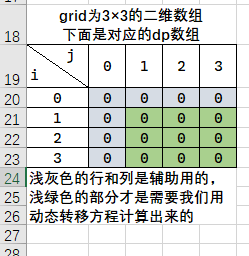
  
  
  多出来的那一行一列本意是想方便迎合之后的状态转移方程中出现的下标取值，但是后来发现这多出来的一行一列不知道该填什么初始值比较好，所以就放弃了，这也导致我们后面必须特意去初始话 dp 数组的第一行和第一列，如果能找到一个合适的初始值，那么下面的程序就将变得更简洁（因为不用特意初始化 dp 数组的第一行和第一列了）。

• 然后就是上面提到的特意初始化 dp 数组的第一行和第一列。因为之后的状态转移方程中用到了 i-1 和 j-1 这样的下标。

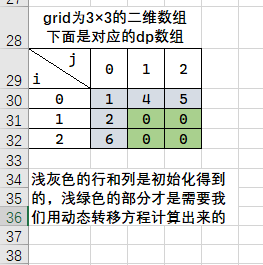
③确定状态转移方程。这也是动态规划中最为关键的一步。这道题目的转移方程还是比较容易就能看出来的。首先根据题意可知， dp[i][j] 是只能根据其上面（dp[i-1][j] ）或左面（dp[i][j-1] ）这两个元素中的一个来计算获取的。我们要做的就是取这这两者中的较小值。然后将获得的较小值与当前网格的值（grid[i][j] ）相加即是 dp[i][j] 的值。也就是：

dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];

④确定对源数据的遍历顺序。这道题中的遍历顺序还是很容易看出来是从前至后，从上到下。

详解请看下方注释。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
  // 创建一个长宽和grid一样的dp二维数组，并同时给每个元素填充 0
  let dp = Array.from({ length: grid.length }).map(
    () => Array.from({ length: grid[0].length }).fill(0)
  );
  // 初始化dp数组的第一个元素
  dp[0][0] = grid[0][0];
  // 初始化dp数组的第一列
  for (let i = 1; i < dp.length; i++) {
    dp[i][0] = dp[i - 1][0] + grid[i][0];
  }
  // 初始化dp数组的第一行
  for (let i = 1; i < dp[0].length; i++) {
    dp[0][i] = dp[0][i - 1] + grid[0][i];
  }
  // 开始由前向后，由上到下地遍历原始的grid数组
  for (let i = 1; i < grid.length; i++) {
    for (let j = 1; j < grid[0].length; j++) {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
    }
  }
  // grid遍历完成后，dp数组的最后一个元素就是我们需要的结果，将其返回
  return dp[dp.length - 1][dp[0].length - 1];
};


提交记录
61 / 61 个通过测试用例
状态：通过
执行用时：88 ms, 在所有 JavaScript 提交中击败了37.34%的用户
内存消耗：41.4 MB, 在所有 JavaScript 提交中击败了9.18%的用户
时间：2021/09/12 10:09	

2、不特意初始化首行和首列

这种解法相当于是把对 dp 数组首行和首列的初始化逻辑放到了遍历过程中，而初始化操作只需要一个简单的 dp[0][0] = grid[0][0] 就可以了。其实本质还是一样的，只是看起来似乎逻辑更通畅一些。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
  let dp = Array.from({ length: grid.length }).map(
    () => Array.from({ length: grid[0].length }).fill(0)
  );
  // 初始化dp数组的第一个元素
  dp[0][0] = grid[0][0];
  // 开始由前向后，由上到下地遍历原始的grid数组
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      if(i === 0 && j === 0) {
        continue;
      }
      // 填充dp数组的第一列
      if(i === 0) {
        dp[i][j] = dp[i][j - 1] + grid[i][j];
        continue;
      }
      // 填充dp数组的第一行
      if(j === 0) {
        dp[i][j] = dp[i - 1][j] + grid[i][j];
        continue;
      }
      // 其他常规dp元素的计算
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
    }
  }
  // 最后结果还是dp数组中的最后一个元素
  return dp[dp.length - 1][dp[0].length - 1];
};

提交记录
61 / 61 个通过测试用例
状态：通过
执行用时：88 ms, 在所有 JavaScript 提交中击败了37.34%的用户
内存消耗：41 MB, 在所有 JavaScript 提交中击败了12.90%的用户
时间：2021/09/12 10:18

可以看到这种做法在空间消耗上还是稍稍比之前的那种做法更好一点的，应该是因为少用了两个 for 循环中的 i 吧。

3、不特意初始化首行和首列—二维解法最终版

在【2、不特意初始化首行和首列】中所说的那种方法确实可以说是不特意单独地把初始化dp数组首行和首列的操作放到遍历过程之外来去做。但是其本质还是对dp数组的第一行和第一列做了一些特殊对待，所以我觉得其实有点强行解释的味道。

在思考下面那种一维数组的解法时，我突然想通了我之前提到的那个问题：【初始化 dp 数组时遇到的小问题（可点击跳转）】。

其实我一开始是用 Infinity 来填充那多出来的一行一列的，但是发现计算 dp[1][1] 时就会出问题（ dp[1][1] 本来应该是 grid[0][0] 的，却变成了 Infinity ），试了填充诸如 0 和 101 （因为题目的【提示】里说了：0 <= grid[i][j] <= 100）之类的值，结果找不到合适的初始值可以达到我预期的要求，总是会有个别元素无法计算出正确结果，导致后面计算出的结果全是错的，所以我才放弃了这种多加一行一列的思路。

但是在做下面【我的题解2（动态规划—一维dp数组；最佳性能）】中的 dp 数组初始化操作时，我却意外发现了合适的初始值。其实就是 Infinity ，但是需要特别对 dp[0][1] 这个元素进行初始化，而且必须初始化为 0。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
  // 创建一个长宽分别比grid大1的dp二维数组，并同时给每个元素填充 Infinity
  let dp = Array.from({ length: grid.length + 1 }).map(
    () => Array.from({ length: grid[0].length + 1 }).fill(Infinity)
  );
  // 初始化dp[0][1]（注意这里是关键的初始化操作，此时dp数组的状态请看下方【补充1】）
  dp[0][1] = 0;
  // 开始由前向后，由上到下地遍历原始的grid数组
  // 注意这里i和j的结束条件不是参考grid的长宽，且grid下标取值也变了，详解看下方【补充2】
  for (let i = 1; i < dp.length; i++) {
    for (let j = 1; j < dp[0].length; j++) {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
    }
  }
  // grid遍历完成后，dp数组的最后一个元素就是我们需要的结果，将其返回
  return dp[dp.length - 1][dp[0].length - 1];
};

提交记录
61 / 61 个通过测试用例
状态：通过
执行用时：72 ms, 在所有 JavaScript 提交中击败了87.31%的用户
内存消耗：40.8 MB, 在所有 JavaScript 提交中击败了17.16%的用户
时间：2021/09/14 13:43	

可以看到，这种解法的时间表现比之前的那两种好了不少，毕竟把初始化 dp 数组的操作大大简化了一波。

相关补充

【补充1】

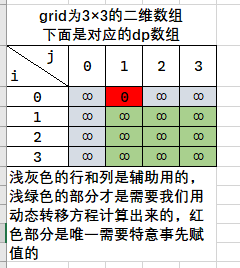
为什么 dp[0][1] 必须初始化为 0 ？其实只要观察计算dp[1][1] 时的过程就可以了，如果 dp[0][1] 也为 Infinity，那么 dp[1][1] = Math.min(dp[0][1], dp[1][0]) + grid[0][0] 的计算结果就会是 Infinity（实际是应该是grid[0][0]），于是后面所有的结果都将计算错误。

【补充2】

因为之前创建的 dp 数组的长宽和 grid 数组的长宽是一样的，所以这里 i和 j 的结束条件参照 dp 和 grid 都可以，但是现在我们创建的 dp 数组的长宽分别比 grid 数组的长宽大 1，所以就要明确指示结束条件是参考 dp 数组的长宽。当然，grid[i][j] 也要改为 grid[i-1][j-1]。

【补充3】

因为这种解法是采用多一行一列的做法的，而之前分析 dp[i][j] 的含义时是没有是不是根据这个结构来分析的，所以在这里 dp[i][j] 的含义应该改为：由起点位置（也就是 grid[0][0]）到 grid[i-1][j-1] 的所有路径和中的那个最小值。

我的题解2（动态规划—一维dp数组；最优解）

一般来说，二维的 dp 数组可以通过滚动数组的方式变为一维 dp 数组，这样就可以大大节省空间。之前我都没有仔细将这个滚动数组到底是怎么样“滚”的，因为实在是不好表述，可能得做一些动画之类的才能讲得非常清晰明白，那非常花时间。之前我也提到过，但是可能不是很清楚，可以参阅下面的博客：

参考：【算法-LeetCode】322. 零钱兑换（动态规划；博采众长的完全背包问题详解；二维数组；滚动数组）_赖念安的博客-CSDN博客
参考：【微信公众号：代码随想录 2021-01-19】动态规划：关于01背包问题，你该了解这些！（滚动数组）

其实只要在二维数组的解法中抓住两个重点：

• dp[i][j] 是来自于 dp[i - 1][j] （也就是 dp[i][j] 的正上方的相邻元素）和 dp[i][j - 1] （也就是 dp[i][j] 正左方的相邻元素）两个元素。
• 每个要计算的 dp[i][j] （那些浅绿色的部分）的初始值是什么都无所谓，因为最后都会被状态转移公式的计算结果覆盖。

就可以理解下面这个滚动数组是怎么来的了。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
  let dp = Array.from({ length: grid[0].length + 1 }).fill(Infinity);
  // 注意这个关键的初始化操作，这里为什么必须初始化为0的原因和上面提到的那个【补充1】一样
  dp[1] = 0;
  // 这里就没得选了，i和j的结束条件只能参照grid的长宽了，因为dp甚至都不是二维的了……
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      dp[j + 1] = Math.min(dp[j], dp[j + 1]) + grid[i][j];
    }
  }
  // grid遍历完成后，dp数组的最后一个元素就是我们需要的结果，将其返回
  return dp[dp.length - 1];
};

提交记录
61 / 61 个通过测试用例
状态：通过
执行用时：64 ms, 在所有 JavaScript 提交中击败了98.21%的用户
内存消耗：39.5 MB, 在所有 JavaScript 提交中击败了86.04%的用户
时间：2021/09/14 13:17

可以看到，这种方法的空间表现远好于之前提到的二维数组的解法，毕竟把二维的空间需求直接压缩到了一维。

官方题解

更新：2021年7月29日18:43:21

因为我考虑到著作权归属问题，所以【官方题解】部分我不再粘贴具体的代码了，可到下方的链接中查看。

更新：2021年9月12日10:21:17

参考：最小路径和 - 最小路径和 - 力扣（LeetCode）

【更新结束】

有关参考

更新：2021年9月12日10:22:55
参考：【算法-LeetCode】53. 最大子序和（动态规划初体验）_赖念安的博客-CSDN博客
更新：2021年9月14日16:39:42
参考：【算法-LeetCode】322. 零钱兑换（动态规划；博采众长的完全背包问题详解；二维数组；滚动数组）_赖念安的博客-CSDN博客
参考：【微信公众号：代码随想录 2021-01-19】动态规划：关于01背包问题，你该了解这些！（滚动数组）

最后

以上就是斯文小鸽子为你收集整理的【算法-LeetCode】64. 最小路径和（动态规划；二维数组；滚动数组）64. 最小路径和 - 力扣（LeetCode）的全部内容，希望文章能够帮你解决【算法-LeetCode】64. 最小路径和（动态规划；二维数组；滚动数组）64. 最小路径和 - 力扣（LeetCode）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。