求逆序对数错误思路: 正确思路：求逆序对数代码：

69 阅读 0 评论 46 点赞

我是靠谱客的博主怡然红酒，最近开发中收集的这篇文章主要介绍求逆序对数错误思路: 正确思路：求逆序对数代码：，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

求逆序对数

总时间限制:

500ms

内存限制:

65536kB

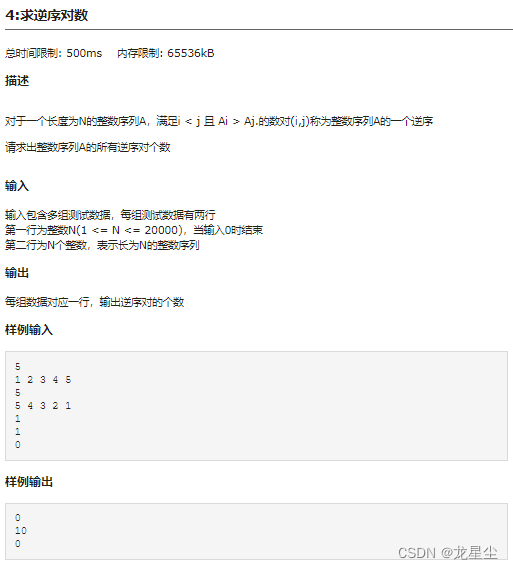
描述

对于一个长度为N的整数序列A，满足i < j 且 Ai > Aj.的数对(i,j)称为整数序列A的一个逆序

请求出整数序列A的所有逆序对个数

输入

输入包含多组测试数据，每组测试数据有两行
第一行为整数N(1 <= N <= 20000)，当输入0时结束
第二行为N个整数，表示长为N的整数序列

输出

每组数据对应一行，输出逆序对的个数

样例输入

样例输出

0
10
0

错误思路:

首先跟大家讲一下，我最开始的时候的思路，首先输入n和a[1~n]，如果n=0就直接break退出了（直接return也是可以的），然后进行双重for循环j=i+1保证i<j的，然后进行判断，如果a[i]>a[j]的话，那么将计数器++，循环过后输出sum就行了。

错误代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
	while(1){
		int n,sum=0;
		cin>>n;
		if(n==0) break;
		int a[n];
		for(int i=0;i<n;i++) cin>>a[i];
		for(int i=0;i<n;i++)
		  for(int j=i+1;j<n;j++)
		    if(a[i]>a[j])
		      sum++;
		cout<<sum<<endl;
	}
	return 0;
}

以上就是我第一次提交的代码（想都没有想到是排序“就算标签上写着”），结果就寄了“Time Limit Exceeded”

错误状态：

正确思路：

经过了这次的超时，我终于想到了排序，我在想:"连我这个O(nlogn)的时间复杂度都寄了，那么冒泡等排序就肯定不行了，于是我想到了快排和归并还有桶"，我是先想效率最快的桶、快排的，但是我实在想不到用快排怎么实现这道题。

之后我只好用归并了：

用分治算法，将序列分成两半，对左边一半求逆序对数，对右边一半求逆序对数，然后求左边一半和右边一半构成的逆序对数。在求逆序对数的时候要对数列进行归并排序，在进行归并排序的同时进行逆序对数的统计。

求逆序对数代码：

#include<bits/stdc++.h>
using namespace std;
const int N=20005;
int merge(int a[],int s,int m,int e) {
    vector<int> a1;
    int m1=s,m2=m+1,c=0;
    while(m1<=m&&m2<=e){
        if(a[m1]>a[m2]){
            c+=m-m1+1;
            a1.push_back(a[m2]);
            m2++;
        }
        else{
            a1.push_back(a[m1]);
            m1++;
        }
    }
    while(m1<=m){
        a1.push_back(a[m1]);
        m1++;
    }
    while(m2<=e){
        a1.push_back(a[m2]);
        m2++;
    }
    int k=0;
    for(int i=s;i<=e;i++) a[i]=a1[k++];
    return c;
}
int solve(int a[],int s,int e) {
    if(s>=e) return 0;
    int m=(s+e)/2;
    int l=solve(a,s,m);
    int r=solve(a,m+1,e);
    int l_r=merge(a,s,m,e);
    return l+r+l_r;
}

int main(){
    int n;
    int a[N];
    while(scanf("%d",&n)&&n!=0){
        for(int i=0;i<n;i++) scanf("%d",&a[i]);
        int sum=solve(a,0,n-1);
        cout<<sum<<endl;
    }
    return 0;
}

这里有一个要注意的点就是传进去的数组是a，a不是一个全局变量，但是递归调用之后a的值会改变。

我之后会继续讲排序的题目（一道比一道难“简单的我就不讲了”）

题目链接：
OpenJudge - 4:求逆序对数http://dsalgo.openjudge.cn/sort/4/