数据结构 （C++）笔记6 （有序列表 & 排序器）有序列表 & 排序器

有序列表 & 排序器

有序列表

若列表中所有节点的逻辑次序与其大小次序完全一致，则称作有序列表。

唯一化

template <typename T> int List<T>::uniquify() { //成批剔除重复元素，效率更高
   if ( _size < 2 ) return 0; //平凡列表自然无重复
   int oldSize = _size; //记录原规模
   ListNodePosi(T) p = first(); ListNodePosi(T) q; //p为各区段起点，q为其后继
   while ( trailer != ( q = p->succ ) ) //反复考查紧邻的节点对(p, q)
      if ( p->data != q->data ) p = q; //若互异，则转向下一区段
      else remove ( q ); //否则（雷同），删除后者
   return oldSize - _size; //列表规模变化量，即被删除元素总数
}

查找

template <typename T> //在有序列表内节点p（可能是trailer）的n个（真）前驱中，找到不大于e的最后者
ListNodePosi(T) List<T>::search ( T const& e, int n, ListNodePosi(T) p ) const {
// assert: 0 <= n <= rank(p) < _size
   /*DSA*/printf ( "searching for " ); print ( e ); printf ( " :n" );
   do {
      p = p->pred; n--;  //从右向左
      /*DSA*/  printf ( " -->%4d", p->data );
   } while ( ( -1 < n ) && ( e < p->data ) ); //逐个比较，直至命中或越界
   /*DSA*/  printf ( "n" );
   return p; //返回查找终止的位置
} //失败时，返回区间左边界的前驱（可能是header）——调用者可通过valid()判断成功与否

排序器

统一入口

template <typename T> void List<T>::sort ( ListNodePosi(T) p, int n ) { //列表区间排序
   switch ( rand() % 3 ) { //随机选取排序算法。可根据具体问题的特点灵活选取或扩充
      case 1:  insertionSort ( p, n ); break; //插入排序
      case 2:  selectionSort ( p, n ); break; //选择排序
      default: mergeSort ( p, n ); break; //归并排序
   }
}

插入排序

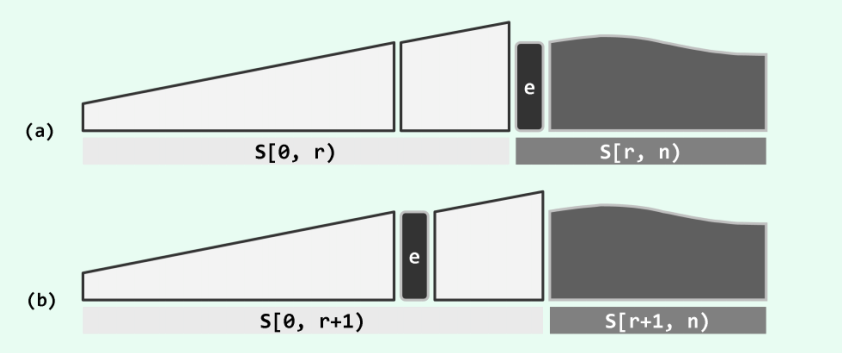
示例程序

template <typename T> //列表的插入排序算法：对起始于位置p的n个元素排序
void List<T>::insertionSort ( ListNodePosi(T) p, int n ) { //valid(p) && rank(p) + n <= size
   /*DSA*///printf ( "InsertionSort ...n" );
   for ( int r = 0; r < n; r++ ) { //逐一为各节点
      insertA ( search ( p->data, r, p ), p->data ); //查找适当的位置并插入
      p = p->succ; remove ( p->pred ); //转向下一节点
   }
}

选择排序

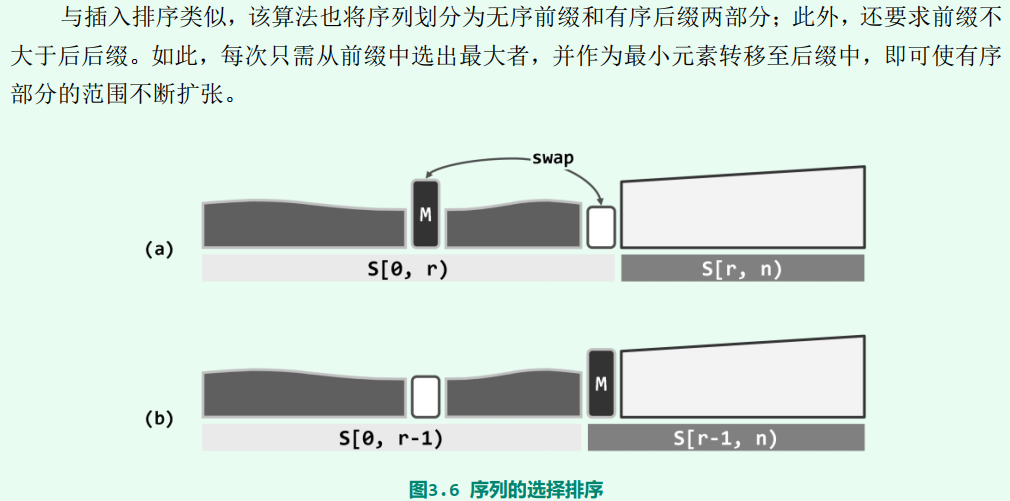
示例程序

template <typename T> //列表的选择排序算法：对起始于位置p的n个元素排序
void List<T>::selectionSort ( ListNodePosi(T) p, int n ) { //valid(p) && rank(p) + n <= size
   /*DSA*///printf ( "SelectionSort ...n" );
   ListNodePosi(T) head = p->pred; ListNodePosi(T) tail = p;
   for ( int i = 0; i < n; i++ ) tail = tail->succ; //待排序区间为(head, tail)
   while ( 1 < n ) { //在至少还剩两个节点之前，在待排序区间内
      ListNodePosi(T) max = selectMax ( head->succ, n ); //找出最大者（歧义时后者优先）
      insertB ( tail, remove ( max ) ); //将其移至无序区间末尾（作为有序区间新的首元素）
      /*DSA*///swap(tail->pred->data, selectMax( head->succ, n )->data );
      tail = tail->pred; n--;
   }
}

template <typename T> //从起始于位置p的n个元素中选出最大者
ListNodePosi(T) List<T>::selectMax ( ListNodePosi(T) p, int n ) {
   ListNodePosi(T) max = p; //最大者暂定为首节点p
   for ( ListNodePosi(T) cur = p; 1 < n; n-- ) //从首节点p出发，将后续节点逐一与max比较
      if ( !lt ( ( cur = cur->succ )->data, max->data ) ) //若当前元素不小于max，则
         max = cur; //更新最大元素位置记录
   return max; //返回最大节点位置
}

归并排序

有序列表的二路归并不仅可以实现，而且能够达到与有序向量二路归并同样高的效率。

template <typename T> //有序列表的归并：当前列表中自p起的n个元素，与列表L中自q起的m个元素归并
void List<T>::merge ( ListNodePosi(T) & p, int n, List<T>& L, ListNodePosi(T) q, int m ) {
// assert:  this.valid(p) && rank(p) + n <= size && this.sorted(p, n)
//          L.valid(q) && rank(q) + m <= L._size && L.sorted(q, m)
// 注意：在归并排序之类的场合，有可能 this == L && rank(p) + n = rank(q)
   ListNodePosi(T) pp = p->pred; //借助前驱（可能是header），以便返回前 ...
   while ( 0 < m ) //在q尚未移出区间之前
      if ( ( 0 < n ) && ( p->data <= q->data ) ) //若p仍在区间内且v(p) <= v(q)，则
         { if ( q == ( p = p->succ ) ) break; n--; } //p归入合并的列表，并替换为其直接后继
      else //若p已超出右界或v(q) < v(p)，则
         { insertB ( p, L.remove ( ( q = q->succ )->pred ) ); m--; } //将q转移至p之前
   p = pp->succ; //确定归并后区间的（新）起点
}

分治策略

template <typename T> //列表的归并排序算法：对起始于位置p的n个元素排序
void List<T>::mergeSort ( ListNodePosi(T) & p, int n ) { //valid(p) && rank(p) + n <= size
   /*DSA*///printf ( "tMERGEsort [%3d]n", n );
   if ( n < 2 ) return; //若待排序范围已足够小，则直接返回；否则...
   int m = n >> 1; //以中点为界
   ListNodePosi(T) q = p; for ( int i = 0; i < m; i++ ) q = q->succ; //均分列表
   mergeSort ( p, m ); mergeSort ( q, n - m ); //对前、后子列表分别排序
   merge ( p, m, *this, q, n - m ); //归并
} //注意：排序后，p依然指向归并后区间的（新）起点

最后两个表示该没有明白，艹~~~.

最后

以上就是淡然火车为你收集整理的数据结构 （C++）笔记6 （有序列表 & 排序器）有序列表 & 排序器的全部内容，希望文章能够帮你解决数据结构 （C++）笔记6 （有序列表 & 排序器）有序列表 & 排序器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。