通俗的解释什么是降维
一些高维度的数据,比如淘宝交易数据,为便于解释降维作用,我们在这假设有下单数,付款数,商品类别,售价四个维度,数据量上百万条,对于下单数和付款数,我们可以认为两者是线性相关的,即知道下单数,我们可以得到付款数,这里很明显这两个属性维度有冗余,去掉下单数,保留付款数,明显能再保证原有数据分布和信息的情况下有效简化数据,对于后面的模型学习会缩短不少时间和空间开销。这就是降维,当然并不是所有数据中都会有过于明显线性相关的属性维度,我们降维后最终的目标是各个属性维度之间线性无关。
降维的要点
首先让特征之间不相关,在不相关中选择最重要的特征(分步方差最大)
先让特征之间线性相关变为不相关(数学上相互垂直的坐标系),在不相关的特征中选择最重要的特征(投射距离最小、分布方差最大)。
每个新特征是所有原特征的线性组合,原特征并没有改变,是特征工程的一个方法
分布方差最大:最大限度的保留了原始数据的原貌
特征值就是分步方差
降维的好处
- 数据压缩(数据在低维下更容易使用处理)
- 消除冗余,去除噪声,降低维度灾难
- 数据噪声:噪声数据是指数据中存在着错误或异常(偏离期望值)的数据,这些数据对数据的分析造成了干扰
- 对于重要的特征能够在数据中明确的显示出来,如果是二维三维便于可视化展示
- 降低算法的开销,提高效率
PCA主成分分析
PCA的全部工作简单点说,就是对原始的空间中顺序地找一组相互正交的坐标轴,第一个轴是使得方差最大的,第二个轴是在与第一个轴正交的平面中使得方差最大的,第三个轴是在与第1、2个轴正交的平面中方差最大的,这样假设在N维空间中,我们可以找到N个这样的坐标轴,我们取前r个去近似这个空间,这样就从一个N维的空间压缩到r维的空间了,但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
所解决的问题
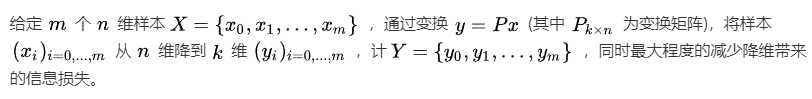
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oHL8nSJ0-1594197562261)(C:Users11515AppDataRoamingTyporatypora-user-images1594195556065.png)]](https://www.shuijiaxian.com/files_image/2023110902/20200708164214234.png)
所依赖的原则
- 降维后的各个维度之间相互独立,即去除降维之前样本
中各个维度之间的相关性。
- 最大程度保持降维后的每个维度数据的多样性,即最大化每个维度内的方差。
核心问题在于协方差矩阵的分解
协方差的含义
可以定义一个表示X,Y相互关系的数字特征,就是协方差
当 c o v ( X , Y ) > 0 时 , 表 明 X 与 Y 正 相 关 当cov(X, Y) > 0时,表明X与Y正相关 当cov(X,Y)>0时,表明X与Y正相关
当 c o v ( X , Y ) < 0 时 , 表 明 X 与 Y 负 相 关 当cov(X, Y) < 0时,表明X与Y负相关 当cov(X,Y)<0时,表明X与Y负相关
当 c o v ( X , Y ) = 0 时 , 表 明 X 与 Y 不 相 关 当cov(X, Y) = 0时,表明X与Y不相关 当cov(X,Y)=0时,表明X与Y不相关
协方差矩阵
最终的优化目标是与特征方差及特征间协方差有密切关系,两者均可以表示为内积的形式,而内积又与矩阵相乘有着密切的关系。
协方差矩阵完美的体现了优化目标中的两个指标
- 方差(对角线)
- 特征相关性(非对角线)
特征值是来描述对应特征向量方向上包含多少信息量的,值越大,信息量(方差)越大
Eig实现PCA的步骤:


Eig分解的前提,矩阵必须为方阵
PCA优缺点
优点:
- 保留绝大部分信息
- 消除评价指标之间的相关影响
- 计算方法简单,易于在计算机上实现
缺点:
- 主成分分析往往具有一定模糊性,不如原始变量的含义那么清楚、确切
SVD奇异值分解
奇异值分解是一个重要的矩阵分解,与之对应的是特征值分解(主成分分析主要使用方法),Eig分解针对的是方阵,对于一般的矩阵就可以用奇异值分解
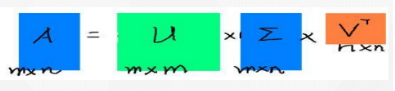
左奇异向量、奇异值、右奇异向量
奇异值分解优缺点
优点:
- 可以简化数据、压缩维度、去除数据噪音、提升算法结果、加快模型计算性能、可以分解任意m*n的矩阵
缺点:
- 转换后的数据比较难理解,如何与具体业务知识对应起来是难点
LDA线性判别分析
LDA是有监督的降维技术
思想
投影后类内方差最小,类间方差最大

LDA与PCA比较

最后
以上就是甜蜜彩虹最近收集整理的关于降维(PCA、SVD、LDA)的全部内容,更多相关降维(PCA、SVD、LDA)内容请搜索靠谱客的其他文章。
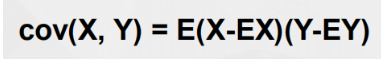








发表评论 取消回复